BI-ML1

Created by Honza Šuráň

Binarni klasifikace

Pokracovani LR

odolna vuci vysoke dimenzionalite
pro priznaku muze stacit trenovacich bodu pro natrenovani
pokud jsou ale priznaky kolinearni, pak $\mathbf{X}^T \mathbf{X}$ bud neni linearni, nebo je vysoce numericky nestabilni, a inverze se pocita blbe

Gini index (Gini impurity)

$GI(\mathcal{D} = 1 - \sum_{i=0}^{k-1}p_i^2 = \sum_{i=1}^{k-1} p_i \cdot (1 - p_i)$
neco jako rozptyl pro Bernoulliho rozdeleni
chci co nejmensi "rozptyl" v podmnozinach - jak moc dobre klasifikovan bude novy prvek/jak moc jsou podmnoziny homogenni

Linearni regrese

predikuje spojitou promennou
predpokladame linearni zavislost vysvetlovane promenne na priznacich
priznaku $X_1, \dots, X_p$ , hodnoty priznaku $x_1, \dots, x_p$
vysvetlovana promenna $Y = w_1 x_1 + \dots + w_p x_p + \epsilon$
$w_1, \dots, w_p$ jsou nezname koeficienty
$\epsilon$ je hodnota nahodnych vlivu
tedy
$Y = w_0 + w_1 x_1 + \dots + w_p x_p + \epsilon$
kde stredni hodnota nahodnych vlivu je 0: $E_\epsilon = 0$
koeficient se nazyva intercept a odpovida ocekavane vychozi hodnote pri nulovych priznacich, napr. v pripade ceny bytu to je cena za zprostredkovani nabidky
mejme , oznacme
$\begin{align} \mathbf{x} &= (x_0, x_1, \dots, d_p)^T \\ \mathbf{w} &= (w_0, w_1, \dots, w_p)^T \end{align}$
pak muzeme zkracene psat
$Y = \mathbf{w}^T \mathbb{x} + \epsilon$

Vyber priznaku

slouzi k redukci priznaku a dimenze
supervizovane i nesupervizovane

Vestavene metody

vyuzivaji model, ktery se trenuje pouze jednou na celych datech a pri tom implicitne provede vyber priznaku
funguje tak, ze se implicitne nauci nektere priznaky vubec nevyuzivat
napr. u linearni regrese jsou prislusne koeficienty odhadnuty jako nulove

Nestrannost metody nejmensich ctvercu

Veta: odhad $\hat{\mathbf{w}}_{OLS}$ ziskany metodou nejmensich ctvercu je za predpokladu $\text{E}_{\mathbf{\epsilon}} = 0$ nestranny, tj. $\text{E} \hat{\mathbf{w}}_{OLS} = \mathbf{w}$
Dukaz:
$\begin{align} \text{E} \mathbf{Y} = \text{E}\left(\mathbf{X} \mathbf{w} + \mathbf{\epsilon} \right) &= \mathbf{X} \mathbf{w} + \text{E} \mathbf{\epsilon} = \mathbf{X} \mathbf{w} \\[7pt] \text{E} \hat{\mathbf{w}}_{OLS} &= \text{E}\left(\mathbf{X}^T X \right)^{-1} \mathbf{X}^T \mathbf{Y} \\ &= \left(\mathbf{X}^T\mathbf{X}\right)^{-1} \mathbf{X}^T \text{E } \mathbf{Y} \\ &= \left(\mathbf{X}^T \mathbf{X}\right)^{-1} \mathbf{X}^T\mathbf{X}\mathbf{w} \\ &= \mathbf{w} \end{align}$
Veta: Predikce je take nestranna:
$\text{E} \hat Y = \text{E} \mathbf{X}^T\hat{\mathbf{w}}_{OLS} = \mathbf{x}^T \text{E} \hat{\mathbf{w}}_{OLS} = \mathbf{x}^T\mathbf{w} = \text{E} Y$
dusledek: vychyleni je nulove:
$\text{bias}\left( \hat{Y} \right) = \text{E} \hat{Y} - \text{E} Y = 0$

Mira neusporadanosti, entropie, informacni zisk

mnozina $\mathcal{D}$ nul a jednicek (ci vice hodnot)
pomery poctu vuci celkovemu mnozstvi, , napr.
1. mira neusporadanosti $\mu$ by mela byt nezaporna
2. pro $(p_0 = 1 \lor p_1 = 1) \Rightarrow \mu = 1$
3. $(p_0 = p_1) \Rightarrow \mu \rightarrow max$
4. rostouci na $[0,\frac{1}{2}]$ , klesajici na $[\frac{1}{2}, 1]$
5. Entropie:
  $H(\mathcal{D}) \begin{cases} 0 \text{ if } p_0 \in \{0, 1\} \\ -p_0 \cdot log(p_0) - p_1 \cdot log(p_1) = -p_0 \cdot log(p_0) - (1-0) \cdot log(1 - p_0) \text{ otherwise} \end{cases}$
pro vice hodnot:
$H(\mathcal{D}) = \sum_{i=0}^{k-1} p_i \cdot log(p_i)$
informacni zisk mnoziny $\mathcal{D}$ podle priznaku , ktery $\mathcal{D}$ deli na $\mathcal{D}_0, \mathcal{D}_1$ s prislusnymi pomery velikosti z puvodni mnoziny :
$IG(\mathcal{D}) = H(\mathcal{D}) - t_0 \cdot H(\mathcal{D}_0) - t_1 \cdot H(\mathcal{D}_1)$

hyperparametry modelu

parametry, ktere urcuji tvar nebo komplexitu modelu: kriterium (gini/entropy), min_samples_split, max_depth, min_ig, ...

Predikce LR

mejme $\hat{w}$ odhad vektoru koeficientu
pak predikujeme hodnotu v konkretnim bode $\mathbf{x}$ vztahem
$\hat{Y} = \hat{\mathbf{w}}^T \mathbf{x} = \hat{w}_0 + \hat{w}_1 x_1 + \dots + \hat{w}_p x_p$
skutecna hodnota (coz je taky nahodna velicina) je ale urcena vztahem
$Y = \mathbf{w}^T \mathbf{x} + \epsilon$
za predopkladu $E_\epsilon = 0$ plati
$E Y = \mathbf{w}^T \mathbf{x}$
$\hat{Y}$ je tedy bodovym odhadem stredni hodnoty v bode $\mathbf{x}$

Hledani vektoru koeficientu

oznacme $L(Y, \hat{Y})$ chybu modelu v bode $\mathbf{x}$ , kde je skutecna hodnota vysvetlovane promenne v bode $\mathbf{x}$ a $\hat{Y} = \mathbf{w}^T \mathbf{x}$ je predikce v bode $\mathbf{x}$
soucet kvadratu odchylek predikci od skutecnych hodnot (residual sum of squares):
$RSS(\mathbf{w}) = \sum_{i=1}^N L(Y_i, \mathbf{w}^T \mathbf{x}_i) = \sum_{i=1}^N (Y_i - \mathbf{w}^T \mathbf{x}_i)^2$

Filtracni metody

vyhodit priznaky, ktere maji prilis nizky rozptyl a jsou tedy temer konstantni
vyhodit priznaky, ktere maji prilis chybejicich hodnot
vyhodit priznaky, ktere spolu hodne koreluji a jsou tedy redundantni
vyhodit priznaky, ktere maji nizkou korelaci s vysvetlovanou promennou (v pripade linearniho modelu!)
u binarnich priznaku muzeme rozdelit vysvetlovanou promennou na 2 skupiny a udelat test hypotezy o rovnosti strednich hodnot - pokud vyjde stejna hodnota, muzeme tento priznak vyhodit

Obalove metody

cilem je vybrat podmnozinu priznaku, pro kterou je vykonnost modelu co nejvetsi - to muze byt benefit, ale hrozi preuceni!
velka vypocetni narocnost - i jen naivni vyber modelu, kde v kazdem chybi priznak, znamena -krat vetsi vypocetni narocnost

Obecne veci ke strojovemu uceni

snaha predikovat vysvetlovanou promennou na zaklade vstupnich dat
pri trenovani se data typicky deli na trenovaci, validacni a testovaci
- trenovaci - slouzi k trenovani modelu, kterych je typicky spousta podle ruznych kombinaci hyperparametru
- validacni - slouzi k vybrani nejlepsiho z modelu, na nichz se trenovala data
- testovaci - slouzi k predikci presnosti na novych datech
trenovaci, validacni a testovaci data by mela byt zcela nezavisla - nejprve data oddelit na 3 separatni mnoziny (typicky treba 60:20:20) a pak az provest trenovani a vyber modelu a odhad presnosti na novych datech
smi se napr. doplnovat chybejici hodnoty medianem/prumerem z trenovacich dat, ale v zadnem pripade se to nesmi prumerovat s validacnimi nebo testovacimi!
preuceni - vlastnost modelu, ktery se prilis soustredi na statisticky nevyznamne vychylky/anomalie v datech, kde by jinak pravdepodobne jina podobna data nemela stejnou hodnotu vysvetlovane promenne s tak optimistickou pravdepodobnosti

Regresni strom

jako kriterium se bere typicky mean squared error
jako kvalitu rozdeleni (informacni zisk) typicky bereme toto:
$\text{MSE}(\mathcal{D}) - t_L \text{MSE}(\mathcal{D}_L) - t_R \text{MSE}(\mathcal{D}_R)$ , kde
$t_L = \frac{\#D_L}{\#D}, t_R = \frac{\#D_R}{\#D}$

Lasso

(Least absolute shrinkage and selection operator)
$\text{RSS}_\lambda^{Lasso} \left(\mathbf{w}\right) = \| \mathbf{Y} - \mathbf{X} \mathbf{w} \|^2 + \lambda \sum_{i=1}^p |w_i|, \lambda \geq 0$
Lasso sdili jakozto jina forma regularizace nektere obecne vlastnosti s modelem hrebenove regrese (bias-variance tradeoff)
pro $\lambda \gt 0$ se bude cilit na vektory $\mathbf{w}$ , ktere maji co nejmensi slozky
nepenalizujeme intercept
neda se derivovat, v mistech, kde je nektera ze slozek nulova, neni funkce diferencovatelna - existuji tedy pouze iterativni metody k hledani $\hat{\mathbf{w}}_\lambda^{Lasso}$
reseni je ridke - nektere ze slozek jsou ciste nuly!
nevyhoda: oproti hrebenove regresi ma u hodne kolinearnich priznaku vybrat pouze nektere z nich

Minimalizace RSS: Derivovani RSS

$\text{RSS} \left( \mathbf{w} \right) = \sum_{i=1}^N \left( Y_i - \mathbf{w}^T \mathbf{x}_i \right) ^2 = \| \mathbf{Y} - \mathbf{X} \mathbf{w} \|^2$

derivujeme RSS:
$\frac{\partial \text{ RSS}}{\partial w_j} = \frac{\partial \sum_{i=1}^N \left(Y_i - \mathbf{w}^T \mathbf{x}_i\right)^2}{\partial w_j}$
derivace souctu (sumy) = soucet derivaci:
$\frac{\partial \text{ RSS}}{\partial w_j} = \frac{\sum_{i=1}^N \partial \left(Y_i - \mathbf{w}^T \mathbf{x}_i\right)^2}{\partial w_j}$
derivace druhe mocniny = $2 \cdot \text{puvodni funkce } \cdot \text{derivace vnitrku}$ :
$\frac{\partial \text{ RSS}}{\partial w_j} = \frac{\sum_{i=1}^N 2 \left( Y_i - \mathbf{w}^T \mathbf{x}_i \right) \partial \left(-\mathbf{w}^T\mathbf{x}_i\right) }{\partial w_j}$
$\mathbf{w}^T\mathbf{x}_i = w_1x_{i;1} + \dots + w_j x_{i;j} + \dots + w_N x_{i;N}$ , pri derivovani jsou ale $w_i; i \neq j$ konstanty a $x_{i;k}$ jsou konstanty vzdy, takze
$\begin{align} \frac{\partial \mathbf{w}^T \mathbf{x}_i}{\partial w_j} &= \frac{d w_1 x_{i;1}}{d w_j} +\dots + \frac{d w_j x_{i;j}}{d w_j} + \dots + \frac{d w_N x_{i;N}}{d w_j} \\ &= 0 + \dots + x_{i;j} + \dots + 0 \\ &= x_{i;j} \end{align}$

Merged prednasky

prednasky-merged.pdf

Rozhodovaci stromy obecne

Vyhody:

nenarocnost na pripravu dat: poradi si s kategorickymi daty i chybejicimi hodnotami
jsou jednoduche, srozumitelne, uceni je relativne rychle a predikce taky
jsou jednoduse interpretovatelne (proc udelaly nejaka rozhodnuti

Nevyhody:

i drobna zmena v trenovacich datech muze znamenat velkou zmenu ve strukture stromu
vetsina implementaci podporuje pouze binarni stromy
najit optimalni strom je NP-uplny problem
je snadne rozhodovaci strom preucit

Parcialni derivace, gradient, Hessova matice

bud $f: \mathbb{R}^d \rightarrow \mathbb{R}$ funkce promennych
parcialni derivace funkce $f(x_1, \dots, x_d)$ podle promenne v bode $\mathbf{a} = (a_1, \dots, a_d) \in \mathbb{R}^d$ definujeme jako derivaci funkce $g(x_i) = f(a_1, \dots, a_{i-1}, x_i, a_{i+1}, \dots, a_d)$ v bode a znacime:
$\partial x_i f(\mathbf{a}) \text{ nebo } \frac{\partial f}{\partial x_i}(\mathbf{a})$
ma-li funkce funkce v bode $\mathbf{a} \in \mathbb{R}^d$ konecne vsechny parcialni derivace, pak definujme gradient funkce v bode $\mathbb{a}$ jako vektor
$\nabla f(\mathbf{a}) = \left( \frac{\partial f}{\partial x_1}(\mathbf{a}), \dots, \frac{\partial f}{\partial x_d}(\mathbf{a}) \right)$
Hessovu matici funkce v bode definujeme takto:
- matice $\mathbf{H}_f(\mathbf{a})$ ma v radku hodnotu $\frac{\partial^2 f}{\partial x_i \partial x_j}(\mathbf{a}) = \left( \frac{\partial}{\partial x_i} \left(\frac{\partial f}{\partial x_j} \right) \right) (\mathbf{a})$

Postacujici podminka pro existenci lokalniho extremu

bud $f: \mathbb{R}^d \rightarrow \mathbb{R}$ funkce promennych a bod $\mathbf{x}^* \in \mathbb{R}^d$ takovy, ze $\nabla f(\mathbf{x}^*) = 0$ a ma na $\cup_{\mathbf{x}^*}$ spojite vsechny druhe parcialni derivace
potom pokud plati
$\left( \forall \mathbf{s} \in \mathbf{R}^d \right) \left( \mathbf{s} \ne \theta \land \mathbf{s}^T \mathbf{H}_f(\mathbf{x}^*)\mathbf{s} \gt 0 \right)$ , tedy matice je pozitivne semi-definitni, pak nabyva funkce v bode $\mathbf{x}^*$ ostreho lokalniho minima
analogicky pro ostre lokalni maximum

Prepis datasetu do maticoveho zapisu

mejme mnozinu paru nezavislych trenovacich dat $(Y_i, \mathbf{x}_i)$ ze stejneho rozdeleni, ktera pochazeji z naseho modelu, tedy $Y_i = \mathbf{w}^T \mathbf{x}_i + \epsilon_i$
zavedme nahodne vektory $\mathbf{Y} = (\mathbf{Y}_1, \dots, \mathbf{Y}_N)^T$ , $\mathbf{\epsilon} = (\epsilon_1, \dots, \epsilon_N)^T$ a body $\mathbf{x}_1, \dots, \mathbf{x}_N$ zapisme po radcich do matice $\mathbf{X} \in \mathbb{R}^{N,p+1}$ :
$\mathbf{X} = \begin{pmatrix} \mathbf{x}_1^T \\ \vdots \\ \mathbf{x}_N^T \end{pmatrix} = \begin{pmatrix} 1 & x_{1;1} & x_{1;2} & \dots & x_{1;p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{N;1} & x_{N;2} & \dots & x_{N;p} \end{pmatrix}$
tedy body v radcich, v jednotlivych sloupcich jsou jednotlive priznaky
pak muzeme napsat $\mathbf{Y} = \mathbf{X} \mathbf{w} + \mathbf{\epsilon}$

Vyhody, nevyhody, tipy a rady

je vhodne volit rozumne , aby se dal delat rozumny odhad a zabranilo se sumu a preuceni
prilis vysoke muze na druhou stranu zpusobit, ze se koukame na prilis mnoho bodu v datasetu, ktere uz tim padem vlastne nejsou az tak blizko bodu, ktery predikujeme
prokleti dimenzionality - pro vyssi dimenzi muze mit (zejmena) euklidovska metrika velice male odchylky pri zmene jednoho treba i dost vyznamneho priznaku - ztrati se v odmocnine mezi ostatnimi cleny, ktere v souctu muzou byt mnohem vyznamnejsi
take s vyssi dimenzi podstatne roste (mame-li interval ) delka intervalu, pokud bychom udelali dokonalou krychli, aby zabirala rekneme celkoveho objemu:
- pro je to , pro je to $\sqrt[2]{0.1} = 0.316$ , pro je to $\sqrt[3]{0.464}$ , pro je to $\sqrt[50]{0.1} = 0.955$ atd.

Forward & backward selection

Forward selection:

Zaciname s $M = \emptyset$ , vezmeme po jednom z priznaku $p_i \notin M$ , natrenujeme pro ruzne mnoziny priznaku $M \cup \{p_i\}$ a vratime , jehoz pridani zpusobilo nejlepsi validacni presnost
dokud jsme si polepsili (pripadne o nejaky threshold) nebo jsme neporusili threshold pro max. pocet priznaku, polozime $M := M \cup \{p'\}$ a opakujeme predchozi bod s mnozinou jeste nevybranych priznaku
slozitost: $\left(p - 1\right) + \left(p - 2\right) + \dots + 1 = \mathcal{O}\left(p^2\right)$ krat rychlost natrenovani jednoho modelu

Backward selection:

funguje uplne stejne, jen zacne se vsemi priznaky a po jednom odebira, dokud nebudeme mit pozadovany pocet a stale doslo ke zlepseni (pripadne pro nejaky threshold)

Rekurzivni odebirani priznaku

model se natrenuje jen jednou a ohodnoti jednotlive priznaky (musi toho byt schopen)
- napr. regrese - maji koeficienty - blizko nule znamena nevyznamny, atd.
nasledne se za linear ku poctu priznaku vyhazou priznaky

tvrzeni o geometrickem stredu

Tvrzeni:

Pro konecnou mnozinu $A \subset \mathbb{R}^p$ plati $\frac{1}{2|A|} \sum_{\mathbf{x}, \mathbf{y} \in A} \| \mathbf{x} - \mathbf{y} \|^2 = \sum_{\mathbf{x} \in A} \| \mathbf{x} - \overline{\mathbf{x}} \|^2 = \min_{\mathbf{\mu} \in \mathbb{R}^p} \sum_{\mathbf{x} \in A} \| \mathbf{x} - \mathbf{\mu} \|^2$
kde $\overline{\mathbf{x}} = \frac{1}{|A|} \sum_{\mathbf{x} \in A} \mathbf{x}$ je geometricky stred (centroid) mnoziny - tedy ze $\overline{\mathbf{x}}$ je optimalni $\mathbf{\mu}$
tedy soucet vzdalenosti od bodu je nejmensi, pokud je dany bod prumerem dat
presne takhle funguje optimum pro MSE

Dukaz:

Pro kazde $\mathbf{a}\ \mathbf{b} \in \mathbb{R}^p$ , protoze $\langle \mathbf{a} | \mathbf{b}\rangle = \mathbf{a}^T \mathbf{b} = \mathbf{b}^T \mathbf{a}$ , plati:
$\| \mathbf{a} - \mathbf{b} \|^2 = \left(\mathbf{a} - \mathbf{b}\right)^T \left(\mathbf{a} - \mathbf{b}\right) = \| \mathbf{a} \|^2 - 2\mathbf{a}^T\mathbf{b} + \| \mathbf{b} \|^2$
pro $\mathbf{a} = \mathbf{x} - \mathbf{\mu}$ a $\mathbf{b} = \mathbf{y} - \mathbf{\mu}$ z toho plyne
$\| \mathbf{x} - \mathbf{y} \|^2 = \| (\mathbf{x} - \mathbf{\mu}) - (\mathbf{y} - \mathbf{\mu}) \|^2 = \| \mathbf{x} - \mathbf{\mu} \|^2 + \| \mathbf{y} - \mathbf{\mu} \|^2 - \left(\mathbf{x} - \mathbf{\mu}\right)^T \left( \mathbf{y} - \mathbf{\mu} \right)$
posledni clen upravime:
$\frac{1}{|A|} \sum_{\mathbf{x}, \mathbf{y} \in A} \left(\mathbf{x} - \mathbf{\mu}\right)^T \left(\mathbf{y} - \mathbf{\mu}\right) = \frac{1}{|A|} \sum_{\mathbf{x} \in A} \left(\mathbf{x} - \mathbf{\mu}\right)^T \sum_{\mathbf{y} \in A}\left(\mathbf{y} - \mathbf{\mu}\right) = \frac{1}{|A|} \left\| \sum_{\mathbf{x} \in A} \left(\mathbf{x} - \mathbf{\mu}\right) \right\|^2$
posledni clen je tedy vzdy nezaporny a roven nule prave, kdyz $\mathbf{\mu} = \overline{\mathbf{x}}$
prohodime-li ve 2. clenu $\mathbf{x}$ a $\mathbf{y}$ , dostaneme prvni clen a po vyscitani pres $\mathbf{y}$ dostaneme:
$\frac{1}{2|A|} \sum_{\mathbf{x}, \mathbf{y} \in A} \| \mathbf{x} - \mathbf{y} \|^2 \leq \sum_{\mathbf{x} \in A} \| \mathbf{x} - \mathbf{\mu} \|^2, \text{ s rovnosti pouze pro } \mathbf{\mu} = \overline{\mathbf{x}}$

Norma

norma vektoru , znacime , je zobrazeni (vsimneme si znaceni - zobrazeni do nezapornych realnych cisel), ktere pro kazde a kazde splnuje nasledujici axiomy:
1. pozitivni definitnost:
  $\| \mathbf{x} \| = 0 \Leftrightarrow \mathbf{x} = \theta$
2. homogenita v absolutni hodnote:
  $\| \alpha \cdot \mathbf{x} \| = \| \alpha \| \cdot \| \mathbf{x} \|$
3. trojuhelnikova nerovnost:
  $\| \mathbf{x} + \mathbf{y} \| \leq \| \mathbf{x} \| + \| \mathbf{y} \|$

Metrika

binarni funkce do realnych cisel:
1. pozitivni definitnost: metrika (vzdalenost) je nulova pouze pro stejne body
2. symetrie:
3. trojuhelnikova nerovnost: $d(x,y) + d(y,z) \geq d(x,y)$ pro kazde $x, y, z \in X$
manhattanska vzdalenost je soucet abs. hodnot rozdilu slozek:
$d\left(\left(1,3,5,6\right), \left(\right)\right)$
nejcastejsi je euklidovska vzdalenost - norma rozdilu vektoru:
$\| \mathbf{x} - \mathbf{y} \|$

Metoda nejblizsich sousedu (kNN)

spoleha na to, ze datove body, ktere maji stejjne nebo (ciselne) podobne parametry, maji vetsi sanci na stejnou binarni predikci pripadne podobnou hodnotu spojite vysvetlovane promenne
hyperparametr - pocet sousedu, metrika $\mathcal{M}$
pomerne dobre vysledky je obcas mozne dosahnout i s nejakou slabsi metrikou, ktera nesplnuje vsechny 3 axiomy (hlavne trojuhelnikovou nerovnost), ale ne vzdy - navic je pak predikce pomalejsi, protoze bez teto vlastnosti data nejde moc chunkovat
je nutne data normalizovat
- standard scaler - naskaluje data, aby byla stredni hodnota 0 a rozptyl
- min-max scaler - nejmensi hodnotu zmeni na nulu, nejvetsi na 1 a mezi nimi udela nejakou interpolaci (typicky linearni)
proces trenovani neni - predikuje se primo na trenovacich datech
pro kazdy datovy bod se vybere nejblizsich sousedu podle metriky $\mathcal{M}$ a predikuje se v pripade binarni klasifikace majoritou, v pripade regrese prumerem

Modely bazovych funkci

linearni model: $\mathbf{x}^T \mathbf{w} +\mathbf{\epsilon}$
je ale mozne vytvorit ruzne funkce $\phi_1, \dots, \phi_M, \phi_i \in \mathbb{R}^p \rightarrow \mathbb{R}^M$ , ktere berou aktualni priznaky a vytvorit z nich nove priznaky
s temito priznaky pak natrenujeme model
vetsinou se pouziva hrebenova regrese, protoze priznaky spis jenom pridavame, nez abychom nahrazovali jiz existujici

Predikce

predikce v bode $\hat{Y}$ :
$\hat{Y} = \hat{\mathbf{w}}_{OLS}^T \mathbf{x} = \mathbf{x}^T \hat{\mathbf{w}}_{OLS} = \mathbf{x}^T (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y}$

Geometricka interpretace

minimalizujeme vzdalenost $\mathbf{Y}, \mathbf{X} \mathbf{w}$ , hledame bod $\mathbf{X} \mathbf{w}$ v podprostoru sloupcu matice $\mathbf{X}$ , ktery je k $\mathbf{Y}$ nejblize
bod $\mathbf{X} \mathbf{w}$ je k $\mathbf{Y}$ nejblize, jestlize je vektor $\mathbf{Y} - \mathbf{X} \mathbf{w}$ na ten podprostor kolmy (ortogonalni projekce)
takovy bod existuje prave 1 (LA2) a existuje tedy globalni minimum (takovy vektor je kolmy na PP a tedy vsechny vektory v nem, viz LA2), tedy
$(\mathbf{X}_{\bullet i})^T(\mathbf{Y} - \mathbf{X} \mathbf{w}) = 0 \quad (\forall i = 0, \dots, p)$
to lze maticove zapsat jako
$\begin{align} \mathbf{X}^T(\mathbf{Y} - \mathbf{X} \mathbf{w}) &= 0 \\ \mathbf{X}^T \mathbf{Y} - \mathbf{X}^T \mathbf{X} \mathbf{w} &= 0 \end{align}$

Pokracovani: Gradient, normalni rovnice, Hessova matice

tedy $\frac{\partial \text{ RSS}}{\partial w_j} = - \sum_{i=1}^N 2\left(Y_i - \mathbf{w}^T\mathbf{x}_i\right) x_{i;j}$
nakonec vyuzijeme toho, jak funguje maticove nasobeni a muzeme to cele zapsat kompaktneji:
$\nabla \text{ RSS} = - \sum_{i=1}^N 2(Y_i - \mathbf{w}^T \mathbf{x}_i) \mathbf{x}_i = -2 \mathbf{X}^T (\mathbf{Y} - \mathbf{X} \mathbf{w})$
polozime-li $\nabla \text{ RSS} = 0$ , ziskame tzv. normalni rovnici: $\mathbf{X}^T \mathbf{Y} - \mathbf{X}^T \mathbf{X} \mathbf{w} = 0$
derivujeme gradient, velice podobne jako pri derivaci $\text{RSS}$ - je konstanta apod.:
$\frac{\partial \nabla \text{ RSS} = - \sum_{i=1}^N 2(Y_i - \mathbf{w}^T \mathbf{x}_i) \mathbf{x}_i}{\partial w_k} = \sum_{i=1}^N 2 x_{i,j} x_{i,k}$
Hessova matice: $\mathbf{H}_{RSS}(\mathbf{w}) = 2\mathbf{X}^T \mathbf{X}$
coz nezavisi na $\mathbf{w}$
dale pro kazde $\mathbf{s} \in \mathbb{R}^{p+1}$ plati: $\mathbf{s}^T(\mathbf{X}^T \mathbf{X}) \mathbf{s}) = (\mathbf{s}^T \mathbf{X}^T) (\mathbf{X} \mathbf{s}) = (\mathbf{X}s)^T(\mathbf{X}s) = \|\mathbf{X}\mathbf{s}\|^2 \geq 0$
Hessova matice je tedy vzdy pozitivne semi-definitni, a proto v kazdem bode, ktery splnuje normalni rovnici, je neostre lokalni minimum RSS

Nesupervizovane uceni

data nemame nijak oznacena, nemame, co predikovat, chceme porozumet strukture
tzn. analyza nejake stabilni struktury datasetu - kde se data vyskytuji, tzn. shlukovani
uvazme situaci, kdy nase -data obsahuji priznaku a oznacme prostor, ve kterem se nachazeji mozne vysledky
- pro binarni priznaky volime $\mathcal{X} = \{0,1\}^p$
- pro spojitych priznaku typicky volime $\mathcal{X} = \mathbb{R}^p$
z pohledu teorie pravdepodobnosti a statistiky chapeme pozorovana data jako realizace nahodneho vektoru $\mathbf{X} = \left(X_1, \dots, X_p\right)^T$
porozumeni vnitrni strukture znamena porozumeni rozdeleni $\mathbf{X}$ 0 chceme ziskat odhad pravdepodobnosti $\text{P}\left(\mathbf{X} \in O\right)$ pro kazdou (rozumnou) podmnozinu $O \subset \mathcal{X}$

Evaluace modelu

Krizova validace

1. bokem si oddelime testovaci data
2. zbytek trenovacich dat  si rozdelime na  podobne velkych 
3. pro kazdou kombinaci hyperparametru :
4.     for J in 1..k:
5.         natrenuj model na datech  s hyperparametry 
6.         na mnozine  odhadni chybu jako 
7.     spocitej cross-validacni chybu pro : 
8. vrat kombinaci hyperparametru  s nejlepsim

typicke volby jsou
muze byt extremne vypocetne narocna
vhodna, pokud je malo dat
pri extremne malem mnozstvi dat lze odhadnout chybu pomoci oddelovani testovaci mnoziny v dalsim vnejsim for cyklu

Shlukovani jako optimalizacni uloha

ucelova funkce - bude ohodnocovat dany rozklad mnoziny na jednotlive shluky
cilem je najit rozklad, ktery ucelovou funkci minimalizuje
pro dane hledame rozklad $C = \left(C_1, \dots, C_k\right)$ na prostoru $\mathcal{X} = \mathbb{R}^p$ vybavenem eukleidovskou vzdalenosti, ktery minimalizuje ucelovou funkci $G\left(C\right)$ :
$G\left(C\right) = \sum_{i=1}^k \frac{1}{2|C_i|} \sum_{\mathbf{x}, \mathbf{y} \in C_i} \| \mathbf{x} - \mathbf{y} \|^2$
tedy je minimalizovan soucet prumeru vzdalenosti bodu v jednotlivych shlucich

Shlukovani

vstupy:
- metricky prostor $\mathcal{X}$ s metrikou
- mnozina dat $\mathcal{D} \subset \mathcal{X}$
- obvykle i pozadovany pocet shluku
vystupy:
- rozklad mnoziny dat na jednotlive shluky: $C = \left( C_1, C_2, \dots, C_k \right)$ , ktere tvori disjunktni sjednoceni $\mathcal{D}$

Konvergence algoritmus k-means

Tvrzeni:

algoritmus k-means v zadne jeho iteraci nezvetsi hodnotu ucelove funkce

Dukaz:

na zaklade predchoziho tvrzeni lze ucelovou funkci vyjadrit jako
$G(C) = \sum_{i=1}^k \sum_{\mathbf{x} \in C_i} \| \mathbf{x} - \overline{\mathbf{x}}_i \|^2, \text{ kde } \overline{\mathbf{x}}_i \text{ je geometricky stred } i \text{-teho shluku}$
Zafixujme $\mathbf{\mu}_i = \overline{\mathbf{x}}_i$ . Vytvorme nove shluky $\tilde{C} = \{ \tilde{C}_1, \dots, \tilde{C}_k\}$ tak, ze bod $\mathbf{x}$ presunume do takoveho shluku $\tilde{C}_i$ , ve kterem je vzdalenost $\| \mathbf{x} - \mathbf{\mu}_i \|$ nejmensi
tim urcite nedojde ke zvetseni souctu kvadratu vzdalenosti:
$\sum_{i=1}^k \sum_{\mathbf{x} \in \tilde{C}_i} \| \mathbf{x} - \mathbf{\mu}_i \|^2 \leq \sum_{i=1}^k \sum_{\mathbf{x} \in C_i} \| \mathbf{x} - \mathbf{\mu}_i \|^2$
z druhe rovnosti predchoziho tvrzeni plyne:
$G\left(\tilde{C}\right) = \sum_{i=1}^k \sum_{\mathbf{x} \in \tilde{C}_i} \left\| \mathbf{x} - \overline{\tilde{\mathbf{x}}}_i \right\|^2 \leq \sum_{i=1}^k \sum_{\mathbf{x} \in \tilde{C}_i} \left\| \mathbf{x} - \mathbf{\mu}_i \right\|^2, \text{ kde } \overline{\tilde{\mathbf{x}}}_i \text{ je geometricky stred shluku } \tilde{C}_i$

problem kolinearity

existuji linearni kombinace sloupcu, ktere daji temer nulkove vektory, zatimco jine linearni kombinace vraci mnohem vetsi vektory: $\| \mathbf{X} \mathbf{u} \| \gg \| \mathbf{X} \mathbf{v} \| \overset{\cdot}{=} 0$ pro nejake $\| \mathbf{u} \| = \| \mathbf{v} \| = 1$
existuji smery, kde ma predikce obrovsky rozptyl a predikce budou dost skakat

Co s tim?

prigenerovat data (muze a nemusi pomoct)
zkusit se zbavit problematickych priznaku
zmenit, co chceme minimalizovat: pridat regularizacni clen → hrebenova regrese

ROC, AUC

bezne model predikuje majoritou (tzn. hodnotu 1 prave tehdy, kdyz je tam vic jednicek
tento parametr $\tau \in \langle 0, 1 \rangle$ muzeme menit, coz zpusobi, ze bude potreba vic/min nez $\frac{1}{2}$ jednicek pro predikci 1
da se na to koukat i jako chozeni po usecce a nastavovani thresholdu pro spadnuti do 0
pro $\tau = 0$ predikujeme same 1,tedy ,
chceme, aby se pro rostouci $\tau$ zmensovalo na ukor , tedy aby se spravne napravovaly predikce a az pak se spatne predikovalo
tento graf vuci $\tau$ se nazyva receiver operating characteristic (ROC krivka):
pro dobry model bude graf strme stoupat k levemu hornimu rohu a pak bude stoupat uz jen velmi pomalu
muzeme spocitat AUC score (area under curve), ktere prave toto pocita

Pokracovani

Implementace ve Scikitu vraci vektor , ktery resi normalni rovnici a zaroven ma co nejmensi normu. Proc to je dobre?
predpokladejme , tedy rovnice je ve tvaru $w_1 x_1 + w_2 x_2 + \dots$ , oznacme $\tilde{w} = w_1 + w_2$ , zaroven tedy $w_1 = w_2 = \tilde{w}$
kdybychom meli predikovat hodnotu pro datovy bod, kde $x_1 \neq x_2$ (napr. a ma velkou normu (treba -krat), predikce by se zvetsila o dost vic, nez jak by se zmenila pro mensi

Jednoznacnost reseni

$\mathbf{X}^T \mathbf{X} \in \mathbb{R}^{p+1, p+1}$
reseni vzdy existuje
navic pokud $\mathbf{X}^T \mathbf{X}$ je regularni, pak reseni existuje prave 1 (jinak jich existuje nekonecne mnoho) a normalni rovnice
$\begin{align} \mathbf{X}^T \mathbf{X} - \mathbf{X}^T \mathbf{X} \mathbf{w} &= 0 \Leftrightarrow \mathbf{X}^T \mathbf{X} \mathbf{w} = \mathbf{X}^T \mathbf{Y} \\ \text{ma potom } &\text{jednoznacne reseni} \\ \hat{\mathbf{w}}_{OLS} &= (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T \mathbf{Y} \end{align}$
protoze plati:
$\mathbf{X}\mathbf{s}=0 \Rightarrow \mathbf{s}^T\mathbf{X}^T\mathbf{X}\mathbf{s}=0 \Rightarrow \|\mathbf{X}\mathbf{s}\|^2=0 \Rightarrow \mathbf{X}\mathbf{s}=0$
jedna se tedy o ekvivalentni tvrzeni a pro nenulove $\mathbf{s}$ nikdy nemuze $\mathbf{X}\mathbf{s}$ vyjit nulove, Hessova matice je tedy pozitivne definitni a $\hat{\mathbf{w}}_{OLS}$ je tedy jedinym globalnim minimem

Algoritmus k-means

problem nalezeni globalniho minima uvedene ucelove funkce je NP-tezky
algoritmus k-means: iterativni algoritmus, ktery konverguje k nejakemu jejimu lokalnimu minimu:

Algoritmus:

Zvolme si stredovych bodu $\mathcal{S}$
Kazdy bod $\mathbf{x}$ prirad do shluku se stredovym bodem $\mathcal{s} \in \mathcal{S}$ takovym, ze $\| \mathbf{x} - \mathbf{s} \|$ je minimalni
$\left(\forall \mathcal{s} \in \mathcal{S}\right)$ : prepocitej stredovy bod $\mathcal{s}$ jako geometricky stred prislusneho shluku
Pokud se shluky nejak zmenily a nebylo dosazeno pripadneho zastavovaciho kriteria, vrat se na bod (2.)

Jak vybrat pocatecni stredove body?

typicky nahodnym vyberem z dat, ktere jsou idealne nejak rozumne od sebe
typicky se algoritmus spusti vickrat a vezme se to shlukovani, kde ma ucelova funkce nejmensi hodnotu

Jak zvolit ?

lze ocekavat, ze pokud "podstrelime" idealni pocet shluku, ucelova funkce se o dost snizi, tedy muzeme pro iterovat, dokud tento graf od bude rozumne klesat
tato metoda muze fungovat, ale casto je pomerne nepouzitelna

Evaluace klasifikacniho modelu

u binarni klasifikace model casto odhaduje pravdepodobnost jako $\hat{p} = \hat{P}(Y = 1 | X = x)$
rozhodovaci strom muze vratit $\hat{p}$ jako relativni pocet reprezentantu tridy z trenovaci mnoziny v listu (jak moc si je jisty)
finalni predikce je tedy
$\hat{Y} = \begin{cases} 1 \text{ pro } \hat{p} > \frac{1}{2} \\ 0 \text{ jinak} \end{cases}$
typicka ztratova funkce "binary cross-entropy loss":
$L(Y, \hat{p}) = -Y \cdot log(\hat{p}) - (1 - Y) log(1 - \hat{p})$
tedy
$L(1, \hat{p}) = -log(\hat{p}), L(0, \hat{p}) = -log(1 - \hat{p})$
prumerna trenovaci chyba (prumerna hodnota ztratove funkce), kde trenovaci mnozina je dvojic :
$\mathcal{L} = \frac{1}{N} \sum_{i=1}^N L(Y_i, \hat{Y}(x_i))$

Evaluacni miry podle presnosti a ocekavaneho vysledku

true positive rate/sensitiva/recall/hit rate - spravne 1 (spravne detekuji nemoc)
false positive rate/false alarm rate/type 1 error rate - v realite 0, ale predikce byla 1 (nekdo zdravy dostane pozitivni vysledek na test)
false negative rate/miss rate/type 2 error rate - v realite 1, ale predikce byla 0 (nepozname, ze je nekdo nemocny)
true negative rate/specificita/selektivita - spravne 0 (spravne necham zdraveho cloveka byt)

Evaluacni miry:

presnost : $P(\hat{Y} = Y) = ACC = \frac{TP + TN}{N}$ - neni vhodna pro nevybalancovane datasety (jinak staci udelat model, ktery predikuje castejsi variantou nezavisle na dalsich vstupnich parametrech a byl by podle tohoto kriteria "dobry", coz je nesmysl)
F1 score: harmonicky prumer precision (positive predictive value): $P(Y = 1 | \hat{Y} = 1)$ a recall: $P(\hat{Y} = 1 | Y = 1)$ , vhodne predevsim pro nevybalancovane datasety, v tomto pripade, kde $\text{P}(Y=1)$ je mensi nez $\text{P}(Y=0)$ :
$F_1 = \frac{2}{1/PPV + 1/TPR} = 2\frac{PPV \cdot TPR}{PPV + TPR}$ $\begin{tikzpicture} \draw (0,0) rectangle (2,2); \end{tikzpicture}$

Hierarchicke shlukovani

na zacatku uvazujeme kazdy bod jako jednotlivy shluk
pokud existuji alespon 2 shluky, najdeme 2 shluky, ktere jsou k sobe nejbliz
tyto 2 shluky spoj do noveho shluku a pokracuj na krok (2.)

Poznamky:

zastavovaci kriterium: pocet shluku
nebo threshold, ktere shluky jeste spojit
zavisi na definici vzdalenosti shluku

Hrebenova regrese

pridani penalizacniho clenu umerneho kvadratu normy koeficientu $\mathbf{w}$ s vynechanim interceptu:
$RSS_\lambda(\mathbf{w}) = \| \mathbf{Y} - \mathbf{X} \mathbf{w} \|^2 + \lambda \sum_{i=1}^p w_i^2$
pro $\lambda = 0$ mame linearni regresi
pro $\lambda > 0$ cilime na nizsi normu vektoru
Zavedme matici
$\mathbf{I}' = \begin{pmatrix} 0 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{pmatrix} \in \mathbb{R}^{p+1,p+1}$
potom
$RSS_\lambda(\textbf{w}) = \| \mathbf{Y} - \mathbf{X} \mathbf{w} \|^2 + \lambda \mathbf{w}^T \mathbf{I}' \mathbf{w}$
gradient:
$\nabla RSS_\lambda(\textbf{w}) = -2\mathbf{X}^T(\mathbf{Y} - \mathbf{X} \mathbf{w}) + 2\lambda \mathbf{I}' \mathbf{w}$
normalni rovnice:
$\mathbf{X}^T \mathbf{Y} - \mathbf{X}^T \mathbf{X} \mathbf{w} - \lambda \mathbf{I}' \mathbf{w} = 0$
Hessova matice
$\mathbf{H}_{{RSS_\lambda}}(\mathbf{w}) = 2 \mathbf{X}^T \mathbf{X} + 2 \lambda \mathbf{I}' = 2(\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}')$

Jednotlive metody

metoda nejblizsiho souseda (single linkage): minimum vzdalenosti bodu z jednotlivych shluku - ma tendenci delat dlouhe retezy
metoda nejvzdalenejsiho souseda (complete linkage): maximum vzdalenosti bodu z jednotlivych shluku - ma tendenci delat kompaktni shluky
parova vzdalenost (average linkage): prumer vzdalenosti mezi kazdou dvojici bodu z ruznych shluku
Wardova metoda: pro kazdou dvojici shluku spocita rozptyl obou shluku vuci prumeru a kdyby doslo ke sjednoceni, cili na maly rozdil rozptylu po sjednoceni, vyuziva euklidovskou vzdalenost

Zkoumame regularitu

Pro kazde $\mathbf{s} \in \mathbb{R}^{p+1}, s \neq \mathbf{0}, \lambda \gt 0$ :
$\begin{align} \mathbf{s}^T(\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}')\mathbf{s} &= (\mathbf{X} \mathbf{s})^T(\mathbf{X} \mathbf{s}) + \lambda \mathbf{s}^T \mathbf{I}' \mathbf{s} \\ &= \| \mathbf{X} \mathbf{s} \|^2 + \lambda \sum_{i=1}^p s_i^2 > 0 \end{align}$
protoze pro $(s_0, \dots, 0)^T \neq \mathbf{0}$ mame $\mathbf{X} \mathbf{s} = (s_0, \dots, s_0)^T \neq \mathbf{0}$
takze $H_{RSS_\lambda}$ je pozitivne definitni a $\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}'$ je regularni
pro $\lambda > 0$ tedy vzdy existuje jednoznacne reseni normalni rovnice $\hat{\mathbf{w}}_\lambda = (\mathbf{X}^T \mathbf{X}+ \lambda \mathbf{I}')^{-1} \mathbf{X}^T \mathbf{Y}$ a odpovida globalnimu minimu $RSS_\lambda$
predikce v bode $\mathbf{x}$ je potom $\hat{Y} = \mathbf{x}^T\hat{\mathbf{w}}_\lambda$

Evaluace pomoci Silhouette skore

uvazujme shlukovani $\mathcal{D} = C_1 \cup \dots \cup C_k$ na metrickem prostoru $\mathcal{X}$ s metrikou a pro libovolny bod $x \in \mathcal{D}$ oznacme index shluku, do ktereho patri, tj. $x \in C_{j(x)}$
pro bod ted muzeme:
- spocitat jako prumernou vzdalenost bodu od vsech ostatnich bodu ve shluku (krome , "vnitrni rozdilnost")
- pro kazdy shluk $C_i; i \neq j(x)$ spocitat prumernou vzdalenost bodu od vsech bodu v , znacime
- spocitat jako minimum z techto prumernych vzdalenosti od ostatnich shluku:
  $b(x) = \min_{i \neq j(x)} d(x, C_i)$
- silhouette skore bodu $x \in \mathcal{D}$ ziskame vztahem
  $s(x) = \frac{b(x) - a(x)}{\max\{a(x), b(x)\}}$
- pokud mame pouze 1 shluk, pak pro kazde $x \in \mathcal{D}$

Pokracovani

oznacme $C_1, \dots, C_k$ mnozinu vsech shluku v $\mathcal{D}$ (vzhledem k $\epsilon$ )
mnozinu $\mathcal{N}$ bodu z $\mathcal{D}$ ( $\mathcal{N} \subseteq \mathcal{D}$ ), ktere nejsou v zadnem ze shluku, nazyvame sumem:
$\mathcal{N} = \mathcal{D} \backslash \bigcup_{i=1}^k C_i$
shluk je tvoren body, ktrere jsou dosazitelne z libovolneho klicoveho bodu, ktery nalezi danemu shluku
okrajovy bod muze byt dosazitelny z klicovych bodu z ruznych shluku:
v takovem pripade ho klidne muzeme uvazovat

Predikce

mejme binarni vysvetlovanou promennou s hodnotami 0 a 1 a priznaku $X_1, X_2, \dots, X_p$ s konstantnim
volime model pro odhad pravdepodobnosti, ktery pro dane hodnoty $\mathbf{x} = \left(x_0, x_1, \dots, x_p\right)$ a pro koeficienty $\mathbf{w} = \left(w_0, w_1, \dots, w_p\right)$ ma tvar
$\text{P}\left(Y = 1 | \mathbf{x}, \mathbf{w}\right) = \frac{e^{\mathbf{w}^T \mathbf{x}}}{1 + e^{\mathbf{w}^T \mathbf{x}}}$
predikuje se 1 prave tehdy, kdyz model vrati $\text{P}\left(Y = 1 | \mathbf{x}, \mathbf{w}\right) \gt \frac{1}{2}$ , jinak 0

Kdy reseni neni jednoznacne

prilis maly dataset: sloupcu pro datovych bodu znamena, ze sloupcu v podprostoru o dimenzi proste LZ budou
nejaky priznak zavisi na ostatnich: napr. priznak, ktery je souctem jinych dvou
one-hot encoding: secteme-li sloupce one-hot encodingu za predpokladu, ze nemame chybejici hodnoty, pak protoze prvni sloupec matice jsou same 1 (pro vychozi hodnotu - intercept), je LZ na sloupcich one-hot encodingu
pak existuje nekonecne mnoho reseni, oznacme dve z nich $\mathbf{w}, \mathbf{w}'$ a plati $\mathbf{X}^T \mathbf{X}(\mathbf{w} - \mathbf{w}') = 0$
podle ekvivalence z minulych uvah ale taky plati $\mathbf{X}(\mathbf{w} - \mathbf{w}') = 0$
pro kazdou dvojici reseni plati:
$\begin{align} RSS(\mathbf{w}) &= \| \mathbf{Y} - \mathbf{X} \mathbf{w} \|^2 \\ &= \| \mathbf{Y} - \mathbf{X} \mathbf{w} + \mathbf{X} \mathbf{w}' - \mathbf{X} \mathbf{w}' \|^2 \\ &= \| \mathbf{Y} - \mathbf{X} \mathbf{w}' - \mathbf{X}(\mathbf{w} - \mathbf{w}') \|^2 \\ &= \| \mathbf{Y} - \mathbf{X} \mathbf{w}' \|^2 \\ &= RSS(\mathbf{w}') \end{align}$

Ensemble metody

DBSCAN - definice

mejme metricky prostor $\mathcal{X}$ s metrikou , ze ktereho pochazi dataset $\mathcal{D}$ a parametry $\epsilon \gt 0$ a $\text{MinPts} \in \mathbb{N}^+$
definujme $\epsilon$ -okoli bodu v $\mathcal{D}$ jako mnozinu
$N_\epsilon(x) = \{y \in \mathcal{D}|d(x,y) \ge \epsilon\}$
bod $x \in \mathcal{D}$ je klicovy bod, jestlize v jeho $\epsilon$ -okoli v $\mathcal{D}$ je alespon $\text{MinPts}$ bodu, tzn.
$|N_\epsilon(x)| \geq \text{MinPts}$
bod $y \in \mathcal{D}$ je primo dosazitelny z bodu $x \in \mathcal{D}$ , jestlize je klicovy bod a $y \in N_\epsilon(x)$ , tj. ma alespon $\text{MinPts}$ bodu v okoli a je jeden z nich
pro dvojici klicovych bodu je relace prime dosazitelnosti symetricka, ale pro tzv. okrajovy bod symetricka neni (takovy bod, ktery neni klicovy, ale je dosazitelny z klicoveho bodu)
bod $y \in \mathcal{D}$ je dosazitelny z bodu $x \in \mathcal{D}$ , pokud v grafu relace prime dosazitelnosti existuje orientovana --cesta
bod $y \in \mathcal{D}$ je spojeny s bodem $x \in \mathcal{D}$ , jestlize existuje klicovy bod $p \in \mathcal{D}$ takovy, ze i jsou dosazitelne z bodu (tzn. existuje orientovana --cesta a orientovana --cesta a orientovana --cesta), jde o symetrickou relaci a pro klicove body i tranzitivni
pro $x, y \in \mathcal{D}$ takove, ze jsou spojene a je klicovy, pak je dosazitelny z
shluk je maximalni mnozina spojenych bodu, formalne shluk je neprazdna podmnozina takova, ze
1. pro kazde $x, y \in \mathcal{D}$ plati, ze pokud $x \in C$ a je dosazitelny z , pak $y \in C$
2. pro kazde $x, y \in C$ je spojeny s (souvislost)

Pokracovani

jednou z moznost je tzv. sigmoida:
$f\left(x\right) = \frac{e^x}{1+e^x} = \frac{1}{1+ e^{-x}}$
tedy pravdepodobnost prislusnosti ke tride v zavislosti na hodnotach priznaku datoveho bodu $\mathbf{x}$ vyjadrime jako
$\frac{e^{\mathbf{w}^T \mathbf{x}}}{1 + e^{\mathbf{w}^T \mathbf{x}}}$
chteli bychom tedy najit takovy vektor koeficientu priznaku $\mathbf{w} = (w_1, \dots, w_p)$ takovy, aby byl tento odhad pravdepodobnosti pomoci $\mathbf{w}$ pro vstupni datovy bod $\mathbf{x}$ co nejblize skutecne pravdepodobnosti

Vazeni datovych bodu

Vazene trenovani:

dalsi stromy se uci na tom, jak dobre/spatne predikovaly ty predchozi
pri uceni stromu se vahy projevi v kroku, kde se pocita informacni zisk (entropie)
pro uzel $\mathcal{D}$ se napr. pro vypocet entropie $H\left(\mathcal{D}_L\right)$ pouzije odhad pravdepodobnosti tridy 1 urceny souctem vah bodu ve tride 1, ktere spadaji do $\mathcal{D}_L$ , podeleny souctem vah vsech bodu v $\mathcal{D}_L$ , lze delat podobne i pro regresni ulohu
pokud mame napr. datove body s vahami $\{0_{0.5}, 1_{0.7}, 1_{0.4}, 0_{0.2}, 1_{0.8}\}$ , pak soucet vah pro je , soucet vsech vah je , tedy pravdepodobnost tridy je v tomto pripade $\frac{2.0}{3.6} = \frac{5}{9}$
tedy u vypoctu entropie se ( obdobne) spocita jako
$\frac{\sum_{i=1}^n w(x) \cdot \text{ pokud }Y_i = 1}{\sum_{i=1}^n w(x_i)} \text{ misto } \frac{\#(Y_i = 1)}{\#Y_i}$
strom se (logicky) snazi lepe predikovat body s vetsi vahou, tedy cim dela vetsi chyby, tim je vetsi penalizace, aby se je priste snazil zmensit

Vazena predikce:

predikuje se , pokud soucet vah pro nadpolovicni, nez soucet vsech vah

Poznamka:

je vhodne mit "weak learners" - modely, ktere casto delaji chyby, ale spise se nepreuci
nemusi jit nutne o rozhodovaci strom, dulezite je, aby model podporoval vazeni dat
redukce vychyleni (bias) - mene systematickych chyb

Vztah vychyleni a rozptylu

plati $\mathbf{Y} = \mathbf{X} \mathbf{w} + \mathbf{\epsilon}$ , kde $\mathbf{\epsilon}$ je nahodny vektor
tedy i odhad vektoru parametru $\hat{\mathbf{w}}_\lambda = (\mathbf{X}^T \mathbf{X} +\lambda \mathbf{I}')^{-1} \mathbf{X}^T \mathbf{Y}$ je nahodny vektor
uvazme pevny bod $\mathbf{x} = (1, x_1, x_2, \dots,x_p) \in \mathbb{R}^{p+1}$ a zkoumejme ocekavanou chybu merenou pomoci kvadraticke ztratove funkce pri predikci $Y = \mathbf{x}^T \mathbf{w} + \mathbf{\epsilon}$ pomoci $\hat{Y} = \mathbf{x}^T \hat{\mathbf{w}}_\lambda$
predpokladejme nezavislost trenovacich a testovacich dat, tedy $\hat{Y}$ a jsou taky nezavisle
z toho plyne
$\begin{align} \text{E} \left( \left( Y - \text{E}Y \right) \left( \text{E}Y - \hat{Y} \right) \right) &= \text{E} \left( Y \left( \text{E}Y \right) - \left( Y \hat{Y} \right) - \left( \text{E}Y \right)^2 + \left( \text{E}Y \right) \hat{Y} \right) \\ &= \color{red}{\left( \text{E}Y \right)^2} - \text{E} \left( Y \hat{Y} \right) \color{red}{- \left(\text{E}Y \right)^2} + \text{E}Y \text{E} \hat{Y} \\ &= -\text{E} \left( Y\hat{Y} \right) + \text{E}Y \text{E}\hat{Y} \\ &=-\text{cov}(Y, \hat{Y}) \\ &= \color{green}{0} \end{align}$
toto plati, protoze jsou a $\hat{Y}$ nezavisle a tedy i nekorelovane, a tedy kovariance je nulova
pro ocekavanou chybu tedy plati
$\begin{align} \text{E} L \left( Y, \hat{Y} \right) &= \text{E} \left( Y - \hat{Y} \right)^2 \\ &= \text{E} \left(\color{green}{(}Y \color{red}{-\text{ E}Y} \color{green}{)} + \color{green}{(} \color{red}{+\text{ E}Y} - \hat{Y} \color{green}{)} \right)^2 \\ &= \text{E} \left( Y - \text{E}Y \right)^2 + 2\text{E} \left( \left( Y - \text{E}Y \right) \left( \text{E}Y - \hat{Y} \right) \right) + \text{E} \left( \hat{Y} - \text{E}Y \right)^2 \\ &= \text{E} \left(Y - \text{E}Y \right)^2 + \color{green}{0} + \text{E} \left( \hat{Y} - \text{E}Y \right)^2 \\ &= \sigma^2 + \text{E} \left( \hat{Y} - \text{E}Y \right)^2 \end{align}$
kde $\sigma^2 = \text{var}(Y) = \text{var}(Y)$ - bayes error, $\text{E} \left( \hat{Y} - \text{E}Y \right)^2$ - mean squared error

Pokracovani

$\begin{align} \text{MSE}\left(\hat{Y}\right) &= \text{E}\left(\hat{Y} - \text{E}Y\right)^2 \\ &= \text{E}\left(\color{red}{\text{E}\hat{Y}}-\text{E}Y+\hat{Y}-\color{red}{\text{E}\hat{Y}}\right)^2 \\ &= \text{E}\left( \text{E}\hat{Y} - \text{E}Y \right)^2 + \text{E}\left(\hat{Y}-\text{E}\hat{Y}\right)^2 + 2\text{E}\left(\hat{Y}-\text{E}\hat{Y}\right)\left(\text{E}\hat{Y}-\text{E}Y\right) \\ &= \left(\text{E}\hat{Y} - \text{E}Y\right)^2 + \text{var}(\hat{Y}) + 2 \cdot 0 \cdot \left(\text{E}\hat{Y} - \text{E}Y\right) \\ &= \left(\text{bias }\hat{Y}\right)^2 + \text{var }\hat{Y} \end{align}$

celkova chyba je tedy $\text{E} L\left(Y, \hat{Y}\right) = \sigma^2 + \left(\text{bias }\hat{Y}\right)^2 + \text{var }\hat{Y}$ (viz nize)
tedy soucet neodstranitelne chyby, kvadratu vychyleni odhadu a rozptylu odhadu
rozptyl: jak moc se podle trenovacich dat meni predikce
vychyleni: systematicke vychyleni
typicky je jedno zvetsuje, druhe zmensuje, chceme minimalizovat soucet

Trenovani - metoda maximalni verohodnosti

Oznacme jako pravdepodobnost, ze datovy bod nabyval hodnoty :
$p_1\left(\mathbf{x}, \mathbf{w}\right) = \text{P}\left(Y = 1 | \mathbf{x}, \mathbf{w}\right) = \frac{e^{\mathbf{w}^T \mathbf{x}}}{1 + e^{\mathbf{w}^T \mathbf{x}}}$
Pak oznacme jako pravdepodobnost, ze datovy bod nabyval hodnoty :
$p_0\left(\mathbf{x}, \mathbf{w}\right) = \text{P}\left(Y = 0 | \mathbf{x}, \mathbf{w}\right) = 1 - \frac{e^{\mathbf{w}^T \mathbf{x}}}{1 + e^{\mathbf{w}^T \mathbf{x}}} = \frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}}}$
Pravdepodobnost, ze -ty datovy bod tedy skutecne nabyval hodnoty (skutecne hodnoty, ktera nastala), se tedy da vypocitat jako
$p_{Y_i} (\mathbf{x}_i, \mathbf{w})$
Predpokladame, ze jednotlive namerene hodnoty jsou na sobe nezavisle, pak (z PST) vime, ze pravdepodnost, ze vsechny jevy nastaly zaroven, se da spocitat jako soucet jednotlivych pravdepodobnosti. Mame fixni trenovaci data $\mathbf{x}$ a muzeme tedy v zavislosti na parametrech $\mathbf{x}$ tuto pravdepodobnost odhadnout jako
$L(\mathbf{w}) = \prod_{i=1}^N p_{Y_i} (\mathbf{x}_i, \mathbf{w})$
Tuto pravdepodobnost chceme maximalizovat.
Teto metode pouzivane pri trenovani modelu logisticke regrese se rika metoda maximalni verohodnosti: Hledame takovy vektor parametru $\mathbf{w}$ , pro ktery je nejvetsi sance, ze trenovaci data nabyvala takovych hodnot, nez pro kterekoliv jine $\mathbf{w}'$ .
Hledame tedy globalni maximum teto verohodnostni funkce $L(\mathbf{w})$

Logisticka regrese

metoda pro klasifikaci, my se omezime na binarni klasifikaci
budeme urcovat pravdepodobnost prislusnosti k dane tride
podobne jako u linearni regrese uvazujme linearni zavislost na jednotlivych priznacich, tentokrat na tom ale zavisi tato pravdepodobnost
oznacme $x := \mathbf{w}^T \mathbf{x} = w_0 + w_1 x_1 + \dots + w_p x_p$ - stejne jako u linearni regrese nejaky intercept + koeficienty priznaku (tedy vektor $(1, w_1, \dots, w_p)$ )
pocitame s tim, ze existuje nejake rozumne rozdeleni roviny na 2 casti (z pohledu vizualizace teto linearni kombinace) s tim, ze cim dal jsme od hranice na jednu stranu, tim vetsi hodnota $\text{P}(Y = 1)$ a naopak cim dal jsme od hranice na druhou stranu, tim mensi hodnota $\text{P}(Y = 1)$
tuto hodnotu chceme nejak rozumne vmestnat do moznych hodnot $\text{P}(Y = 1)$ , coz je interval , a to tak, aby nepresnost u hodne kladne nebo hodne zaporna hodnota nezmenila fakt, ze ta si je model hodne jisty

bias-variance tradeoff u hrebenove regrese

u hrebenove regrese s $\lambda \rightarrow \infty$ vychyleni roste a rozptyl klesa:
pro $\lambda = 0$ mame beznou linearni regresi: nejvetsi rozptyl, zadny bias
pro $\lambda \rightarrow \infty$ nas logicky zajima norma tech koeficientu, tzn. data nas zajimaji min a min → rozptyl klesa, ale mame vetsi systematickou chybu (budeme systematicky predikovat o neco jinak)
knn: s $k \rightarrow n$ se snizuje taky rozptyl a zvetsuje bias
rozhodovaci strom: s vetsi hloubkou se snizuje rozptyl a snizuje bias

Dendrogram

binarni strom, ktery reprezentuje jednotlive kroky shlukovani, pokud algoritmus nema zadany max. pocet shluku
listy jsou mnoziny s pocatecnimi body
koren je cely dataset
jednotlive vrcholy jsou disjunktnim sjednocenim prave dvou vrcholu, a to prave tech, ktere algoritmus sjednotil na tento novy vrchol
kazdy vrchol, ktery neni list, ma v sobe zaroven ciselnou hodnotu, ktera urcuje vzdalenost tech dvou mnozin vrcholu, ktere byly sjednoceny v tento vrchol
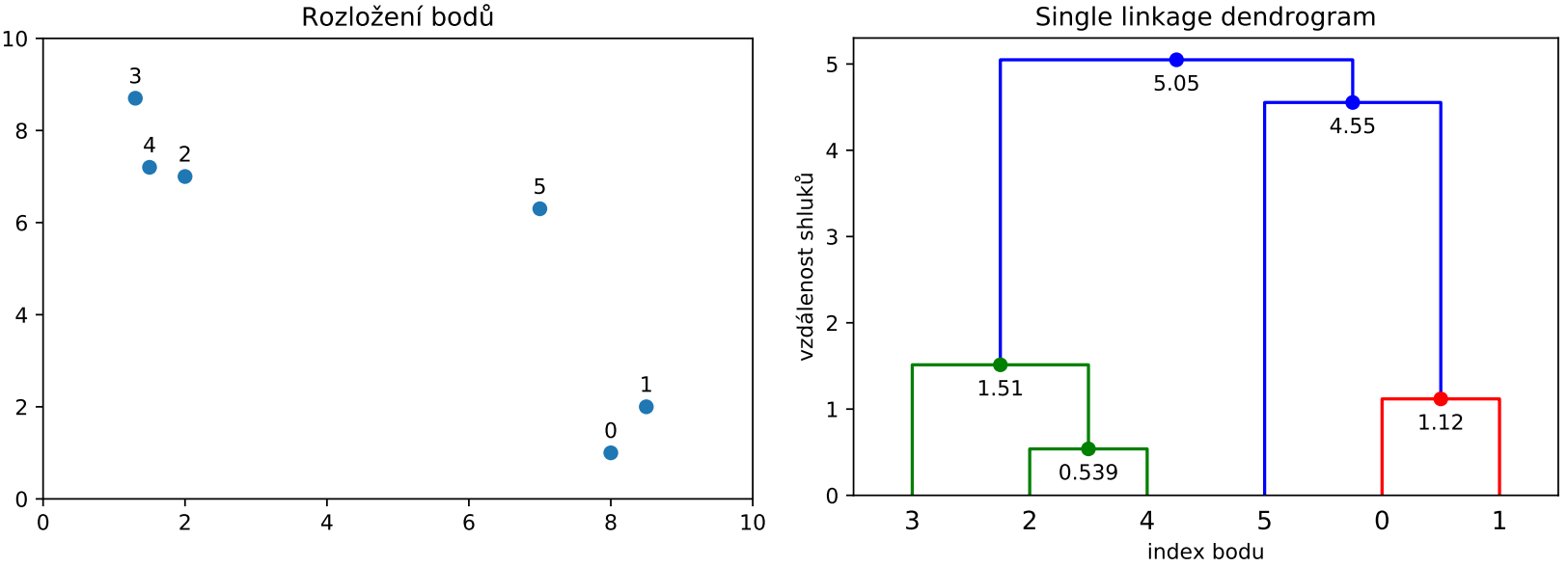
pokud chceme shluku, pak dendrogram usekneme pod -tym nejvyssim vrcholem (pro 1 shluk nic nesekame, pro 2 shluky pod 1., pro 3 shluky pod 2., …) a hrany, ktere toto "useknuti" protne, vedou smerem dolu do prave tech shluku
zaroven lze nastavit threshold, coz je proste -souradnice, na niz se seka
zaroven se da porovnat vysky dvou sousednich vrcholu v ramci osy , coz znaci, o kolik by se musel zvetsit threshold pro spojeni, aby se spojil ten vyssi z tech vrcholu

Nahodne lesy

ze vstupniho trenovaciho datasetu $\mathcal{D}$ vytvorime datasetu $\mathcal{D}_1, \dots, \mathcal{D}_n$ (obvykle stejne velkych jako $\mathcal{D}$ ) pomoci metody bootstrap - vyberu s opakovanim
na kazdem datasetu $\mathcal{D}_i$ naucime rozhodovaci strom, typicky vybereme jen nejaky zlomek priznaku: $Q_1, \dots, Q_n$
pri predikci predikuji pomoci vsech stromu a predikce zprumeruji
muzu zaroven delat vazeny prumer, jak moc si je dany strom jisty
hyperparametry: pocet lesu, pomer $\frac{\left| \mathcal{D}_i\right|}{\left|\mathcal{D}\right|}$ , parametry pro stromy, pomer/pocet (predem nahodne vybranych) featur
prumeruji se nezavisla data, cimz se redukuje rozptyl
odolnejsi vuci preucenim
horsi interpretovatelnost
pomalejsi na natrenovani

Pokracovani silhoutte skore

plati, ze $-1 \leq s(x) \leq 1$
pro :
- $s(x) \gt 0$
- nikdy nebude vetsi nez ve jmenovateli
- $s(x) \gg 0$ : prumerna vzdalenost k jinemu nejblizsimu clusteru je vetsi nez k aktualnimu → GOOD
pro
- $s(x) \lt 0$
- nikdy nebude v abs. hodnote vetsi nez
- $s(x) \ll 0$ : prumerna vzdalenost k jinemu nejblizsimu clusteru je mensi nez k aktualnimu (existuje blizsi cluster) → BAD
pro :
- bod je typicky blizko hranici, napr. okrajovy bod pri DBSCAN
dobre u k-means a average linkage, u DBSCANu muze byt horsi, pokud jsou tvary hodne rozplacnute

DBSCAN - algoritmus

Pro zadane $\epsilon$ spocitej $\epsilon$ - okoli kazdeho bodu a identifikuj klicove body
Vytvor zarodky shluku: Spoj sousedni (primo dosazitelne) body do shluku
Pro kazdy bod, ktery neni klicovy: Pridej ho do shluku podle klicoveho bodu v okoli, pokud nejaky existuje, jinak ho pridej mezi sum

Poznamky:

Pokud ma nejaky okrajovy bod vice klicovych bodu ve svem $\epsilon$ -okoli vice ruznych zarodku shluku, spadne do prvniho shluku, ke kteremu se algoritmus dostane
lze ukazatm ze slozitost je v nejhorsim pripade $\mathcal{O}\left(n^2\right)$ , v mnoha realnych situacich se ale realne dostane na $\mathcal{O}\left(n \log n\right)$
hyperparametry: $\text{MinPts}, \epsilon$ , kde $\epsilon$ je typicky dulezitejsi
$\text{MinPts}$ je dobre volit 4-6, nekdy $2, \dots, p$ , kde je pocet priznaku
$\epsilon$ je dobre volit male, lze napr. volit prumernou vzdalenost bodu k jejich $\left(2 \cdot p-1\right)$ -temu sousedovi
sum by mel byt mezi 1 % a 30 %
neni dobre mit velke shluky (napr. pres 50 % velikosti datasetu)

Zaver silhouette skore

pomoci pro kazde $x \in \mathcal{D}$ lze ted napriklad zpocitat prumerne silhouette skore pro shluk , znacime
nebo prumerne skore pro cele shlukovani, znacime
porovnani pro ruzne pocty shluku muzeme pouzit k nalezeni vhodneho poctu shluku jako hodnoty, pri ktere je minimalni

Analyza asociacnich pravidel

cilem je nalezt spolecne hodnoty priznaku $X = \left(X_1, \dots, X_p\right)^T$ - nalezeni oblasti prostoru, kde se data vyskytuji s velkou pravdepodobnost
mozne vyuziti je v doporucovacich systemech
nejcasteji se zabyvame pouze oblastmi, ktere jsou ve tvaru kartezskeho soucinu pro jednotlive priznaky, tj. chceme, aby byla pravdepodobnost $\text{P}\left( \cap_{j=1}^p \left( X_j \in s_j \right) \right)$ relativne velka, tj. casto zkoumame kartezsky soucin spojitych podintervalu rozsahu jednotlivych priznaku (napr. $\langle1, 2\rangle$ pro priznak a zaroven $\langle3,5\rangle$ pro priznak )
prunik takovych podmnozin priznaku: $\cap_{j=1}^p \left( X_j \in s_j \right)$ se nazyva konjunktivni pravidlo

AdaBoost

1. Nastavme vahy rovnomerne, tedy  a polozme 
2. Pokud :
     Nauc strom  na datech  s vahami 
3. Do promenne  ulozme soucet vah tech bodu z ,
   ktere jsou spatne klasifikovane stromem 
4. Pokud :
     Algoritmus skonci (vsechna data jsou natrenovana spravne)
     a vrati rozhodovaci stromy 
5. Polozme 
     kde  je hyperparametr modelu zabranujici preuceni
     (pokud je mensi nez 1)
     pokud je malo chyb (), pak 
     pokud je hodne chyb (), pak 
6. Pro stromem  spatne klasifikovane body :
     
7. znormalizujeme vahy, aby jejich soucet byl 1
8. zvetsime  o jedna, vratime se do bodu 2

Maximalizace verohodnostni funkce

tato funkce $L(\mathbf{w})$ se spatne derivuje (je to polynom velkeho stupne)
Pokud to cele obalime logaritmem, ktery je ostre rostouci funkce, bude funkce nabyvat maxima ve stejne hodnote (nijak si neuskodime). Derivuje se to ale mnohem lepe, protoze logaritmus soucinu je soucet logaritmu:
$\begin{align} \mathcal{l}\left(\mathbf{w}\right) &= \text{ln } L\left(\mathbf{W}\right) \\ &= \sum_{i=1}^N \text{ln } p_{Y_i}\left(\mathbf{x}_i, \mathbf{w}\right) \\ &= \sum_{i=1}^N \left(Y_i \text{ln } p_1\left(\mathbf{x}_i, \mathbf{w}\right) + \left(1 - Y_i\right) \text{ln } p_0\left(\mathbf{x}_i, \mathbf{w}\right)\right) \\ &= \sum_{i=1}^N \left( Y_i \text{ln }\left( \frac{e^{\mathbf{w}^T \mathbf{x}_i}}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \right) + \left(1 - Y_i\right) \text{ln }\left( \frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \right) \right) \\ &= \text{... trocha carovani s logaritmem...} \\ &=\sum_{i=1}^N \left(Y_i \mathbf{w}^T \mathbf{x}_i - \text{ln }\left(1 + e^{\mathbf{w}^T \mathbf{x}_i}\right) \right) \end{align}$
pro nebo zde bude prave jeden clen a ten druhy zmizi, coz nam umoznuje kompaktnejsi zapis
hledame gradient teto funkce, abychom mohli hledat jeji extremy

Binarni AAP

casto se AAP aplikuje v pripade binarnich priznaku, tj. $X_j \in \{0,1\}$ - "analyza nakupniho kosiku" (ANK)
pouziva se dalsi omezeni: je bud jednoprvkova mnozina $\{1\}$ , nebo vsechny moznosti daneho priznaku (priznak vypadne) - vybirame pouze priznaky s hodnotou 1, nikoli s hodnotou 0
ekvivalentne tedy hledame mnozinu indexu $\mathcal{K} \subseteq \{1, \dots, p\}$ tak, ze tato pravdedobnost je relativne velka: $\text{P} \left( \cap_{j \in \mathcal{K}} \left( X_j = 1 \right) \right) = \text{P}\left(\prod_{j \in \mathcal{K}} X_j = 1\right)$
mnozina $\mathcal{K}$ se pak nazyva mnozina polozek
relativni velikost polozek v datasetu, ktere danou mnozinu polozek obsahuji, se znaci $T(\mathcal{K})$ a nazyva podpora mnoziny polozek a odpovida odhadu vyse uvedene pravdepodobnosti: $T(\mathcal{K}) = \hat{\text{P}}\left(\cap_{j \in \mathcal{K}}\left(X_j = 1\right)\right) = \frac{1}{N} \sum_{i=1}{N} \prod_{j \in \mathcal{K}} x_{i;j}$
tedy relativni velikost datasetu, ktere odpovidaji teto mnozine polozek

Hledani nad urcitou mez

pri provadeni ANK hledame vsechny mnoziny polozek, pro ktere je podpora vetsi nez nejaka zvolema mez : $\left\{ \mathcal{K}_\mathcal{l} | T(\mathcal{K}_\mathcal{l} \gt t \right\}$
k nalezeni reseni se pouziva efektivni algoritmus "Apriori algoritmus" (implementaci si jde kdyztak vygooglit)
pro kazdou mnozinu polozek $\mathcal{K}$ , kterou nam algoritmus vrati, hledame vhodne rozlozeni na dve disjunktni podmnoziny $A, B; A \cup \mathcal{K}$ , ktere budeme nazyvat asociacni pravidlo (AP) a budeme je znacit $A \Rightarrow B$ , kde nazveme predpoklad a nazveme zaver
podporu takoveho AP definujeme jako podporu sjednoceni $\mathcal{K} = A \cup B$ (rel. velikost $\mathcal{K}$ v datasetu)
spolehlivost je definovana jako podpora pravidla podelena podporou predpokladu:
$C(A \Rightarrow B) = \frac{T(A \Rightarrow B)}{T(A)}$
tedy odhad podminene pravdepobnosti za podminky
AP volime tak, aby spolehlivost byla vyssi nez nejaka zvolena mez
finalnim vystupem asociacni analyzy pravidel je mnozina AP, ktera splnuji
$T(A \Rightarrow B) \gt t \land C(A \Rightarrow B) \gt c$

Hledani gradientu

tuto sumu (soucet) lze derivovat jako soucet derivaci (vnitrku sumy) pro kazde $i \in \{1, \dots, N\}$ , protoze se jedna o rozdil, muzeme oba cleny te vnejsi zavorky derivovat zvlast a odecist je od sebe
pri pocitani parcialni derivace :
- $\mathbf{w}^T \mathbf{x}_i$ je skalarni soucin:
  $\sum_{k=1}^p w_k x_{i;k} = w_1 x_{i;1} + \dots + w_j x_{i;j} + \dots + w_k x_{i;k}$
- vse krome -teho clenu je konstanta (nezavisle na ) a zderivuje se na nulu, -ty clen $w_j x_{i;j}$ se podle zderivuje na $x_{i;j}$
- tedy derivace $Y_i \mathbf{w}^T \mathbf{x}_i$ , protoze je konstanta (nezavisle na ), je $Y_i x_{i;j}$
- derivace $\ln \left(1 + e^{\mathbf{w}^T \mathbf{x}_i}\right)$ :
  $\begin{align} \frac{\partial \ln \left(1 + e^{\mathbf{w}^T \mathbf{x}_i}\right)}{w_j} &= \frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \cdot \frac{\partial \left(1 + e^{\mathbf{w}^T \mathbf{x}_i}\right)}{w_j} \;\;\;\;\; \text{(derivace logaritmu a slozene funkce)}\\ &= \frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \cdot \frac{\partial \, e^{\mathbf{w}^T \mathbf{x}_i}}{w_j} \;\;\;\;\; \text{(derivace souctu jako soucet derivaci)} \\ &= \frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \cdot e^{\mathbf{w}^T \mathbf{x}_i} \cdot\frac{\partial \mathbf{w}^T \mathbf{x}_i}{w_j} \;\;\;\;\; \text{(derivace exponencialy)} \\ &=\frac{1}{1 + e^{\mathbf{w}^T \mathbf{x}_i}} \cdot e^{\mathbf{w}^T \mathbf{x}_i} \cdot x_{i;j} \;\;\;\;\; \text{(derivace skalarniho soucinu, viz vyse)} \\ &= p_1(\mathbf{x}_i, \mathbf{w}) \cdot x_{i;j} \;\;\;\;\; \text{(podle nasi definice } p_1 \text{)} \end{align}$

Hranice

$P\left(Y = 1|\mathbf{x}, \mathbf{w}\right) = \frac{1}{2} \Leftrightarrow \mathbf{w}^T \mathbf{x} = w_0 + w_1 x_1 + \dots + w_p x_p$

resenim takove rovnice je nadrovina v prostoru $\mathbb{R}^p$ (bod v $\mathbb{R}^1$ , primka pro $\mathbb{R}^2$ , rovina pro $\mathbb{R}^3$ )
tato data musi byt hezky linearne separabilni, tj. existuje nadrovina, ktera je spolehlive oddeli na nuly a jednicky (ve 2D primka, ve 3D rovina atd.)
- napr. pokud mame dataset, kde data jsou rovnomerne rozdelena do nejake vzdalenosti od bodu napr. s hodnotou v prvnim a tretim kvadrantu, s hodnotou ve druhem a ctvrtem kvadrantu, nelze je nijak oddelit primkou!!!

Pokracovani

u nalezenych pravidel dale muzeme merit zdvih: odhad $\frac{\text{P}(B|A)}{\text{P}(B)}$ (kolikrat se zvedne pst. , pokud vime, ze nastalo :
$L(A \Rightarrow B) = \frac{C(A \Rightarrow B)}{T(B)}$
pokryti odpovida odhadu podminene pravdepodobnosti - tedy jaka je pst., ze bylo zpusobene :
$\text{Coverage}(A \Rightarrow B) = \frac{T(A \Rightarrow B)}{T(B)}$

Trenovani + predikce

Parametry modelu:
  n: pocet lesu
  k: pocet vybranych prvku
  q: pocet nahodne vybranych priznaku
  H: hyperparametry stromu

Trenovani(D: dataset) -> void:
1. for i = 1..n:
2.    D_i = []
3.    Q_i = vyber nahodnych q priznaku z priznaku D
4.    repeat k times:
5.       x = vyber nahodny prvek z D
6.       D_i.append(x.vyber_priznaky(Q_i))
7.    T_i = natrenuj strom s daty D_i a hyperparametry H

Predikce(x: datovy bod) -> float
1. pro i = 1..n:
2.    Y_i = T_i.predict(x.vyber_priznaky(Q_i))
3. return mean(Y_i)

Predikce

1. Kazdemu stromu  prirad vahu  z kroku 5 trenovaciho algoritmu
2. Secti vahy  vsech stromu, ktere pro  predikuji 
   a to same udelej pro stromy predikujici  (vazena predikce)
3. Rozhodni se pro tu z moznosti, pro kterou je soucet vah vyssi

Priklad

asociacni pravidlo $\{\text{parky}\} \Rightarrow \{\text{horcice}, \text{chleb}\}$
podpora znamena, ze v celem datasetu si koupilo $6 \%$ kombinaci vsech tri produktu
pokud se parky vyskytuji v $8 \%$ pripadu, pak spolehlivost se vypocita jako
$\frac{0.06}{0.08} = 75 \%$
tedy pokud si zakaznik koupi parky, pak v $75 \%$ pripadu si koupi i horcici a chleb
pokud se horcice a chleb vyskytuji v $15 \%$ pripadu, zdvih bude $\frac{0.75}{0.15} = 5$
tedy pokud si zakaznik koupi parek, pak je $5\times$ vetsi sance, ze si koupi horcici a chleb, nez kdyby si parky nekoupil
pokryti je $\frac{0.06}{0.15} = 40 \%$ , tedy ze $40 \%$ lze horcici a chleb brat jako dusledek koupe parku
nevyhoda na podporu je, ze pravidla s velkou hodnotou spolehlivosti i zdvihu, ale s nizkou podporou, nebudou nalezena, napr. $\{\text{doutnik}\} \Rightarrow \{\text{rum}\}$

Hledani gradientu - pokracovani

celkove tedy
$\frac{\partial \, l}{\partial w_j}(\mathbf{w}) = \sum_{i=1}^N \left(Y_i \cdot x_{i;j} - p_1(\mathbf{x}_i, \mathbf{w})_i \cdot x_{i;j} \right) = \sum_{i=1}^N x_{i;j} \left( Y_i - p_1(\mathbf{x}_i, \mathbf{w} \right)$
pomoci maticoveho nasobeni lze gradient prepsat do tvaru
$\nabla \mathcal{l}\left(\mathbf{w}\right) = \mathbf{X}^T\left(\mathbf{Y} - \mathbf{P}\right)$
kde $\mathbf{P} = \left(p_1\left(\mathbf{x}_1, \mathbf{w}\right), p_1\left(\mathbf{x}_2, \mathbf{w}\right), \dots, p_1\left(\mathbf{x}_N, \mathbf{w}\right)\right)^T$
to dost pripomina linearni regresi, kde je $\mathbf{X} \mathbf{w}$ misto $\mathbf{P}$ - oboji to jsou ale hodnoty predikci
nicmene rovnice $\mathbf{X}^T (\mathbf{Y} - \mathbf{P}) = 0$ se neda pocitat analyticky, takze se musi pouzit gradientni sestup, vicerozmerna Newtonova metoda apod.