DM

Created by Nataliia Korop

Malá poznámka o způsobu zápisu permutace

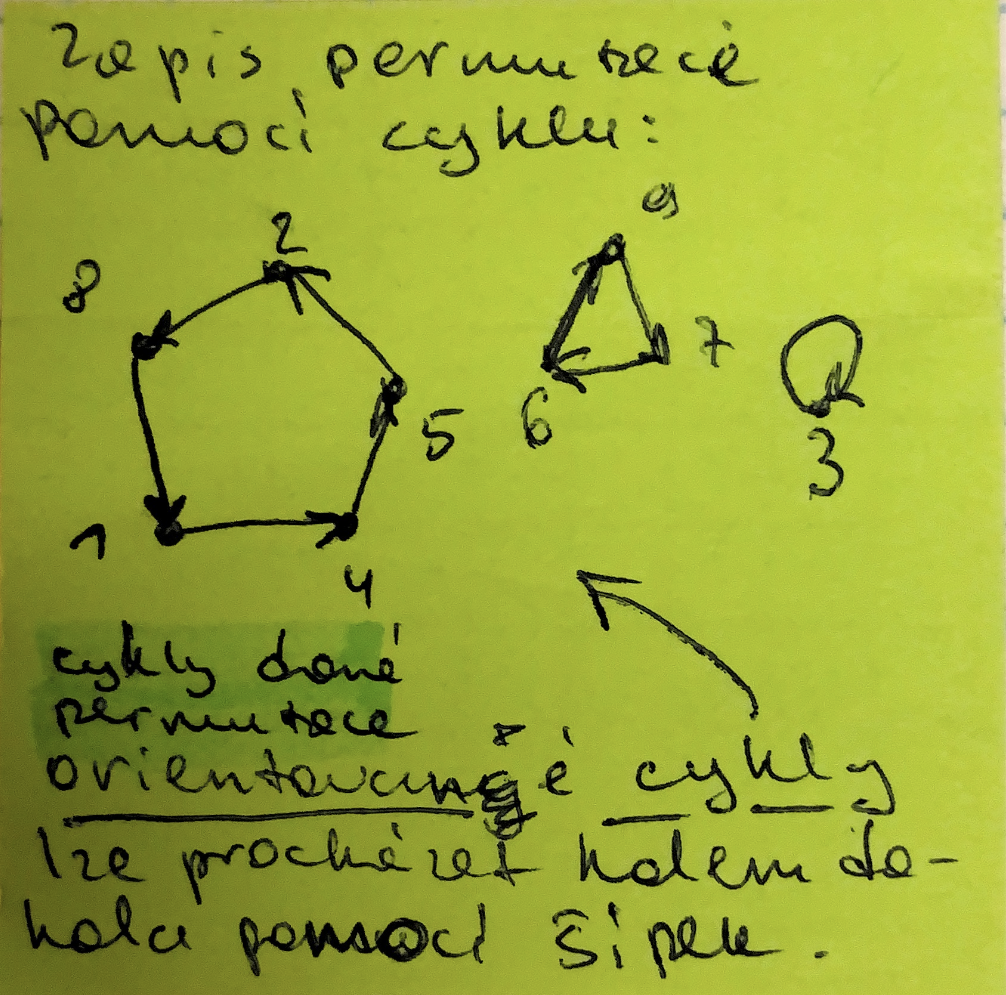
pomocí principu bijekce

Tvrzení o počtu sudých a lichých podmnoži

• Nechť n ≥ 1 každá n-prvková množina má právě 2^n-1 podmnožin sudé velikosti
• S = {A ⊆ N | |A| sudé}, L = {A ⊆ N | |A| liché}

Příklad: X = {1, 2}, S = {∅, {1, 2}}, L = {{1}, {2}}

Důkaz: sestrojím bijekci f mezi S a L, pak musí dle principu bijekce platí |L| = |S|, zvolíme libovolný x ∈ N, ∀ A ∈ S f(A) = A XOR {x} = A ∪ {x} pokud x !∈ A nebo A \ {x} pokud x ∈ A (stejně zprava doleva)

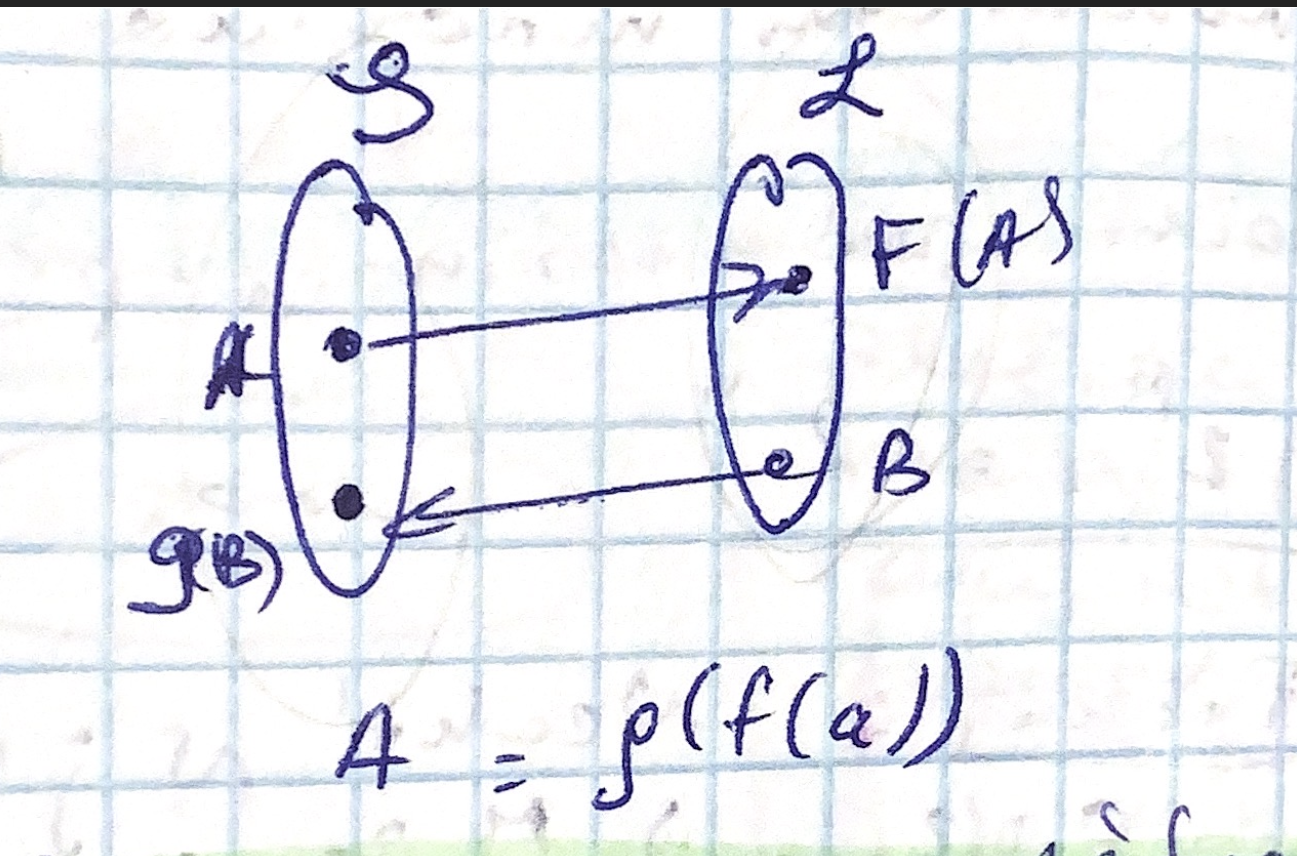
Princip bijekce

• pokud mezi konečnými množinami A a B existuje bijekce, tak mají stejný počet prvků. Speciálně tedy, bývá jedno, jestli [n] je konkretní množina {1, ..., n} nebo libovolná jiná n=prvková množina
• Jinými slovy: pokud ∃ f: A -> B, A, B jsou konečné a f je bijekce,  pak |A| = |B|

Důkaz: f je bijekce, a proto je na a zároveň prostá:

• (na) ∀ b ∈ B ≥ 1 šipek 
• (prostá) ∀ b ∈ B ≤ 1 šipek   => ∀ b ∈ B ∃! šipka z A = # šipek do B = |B| = # šipek z A = |A|

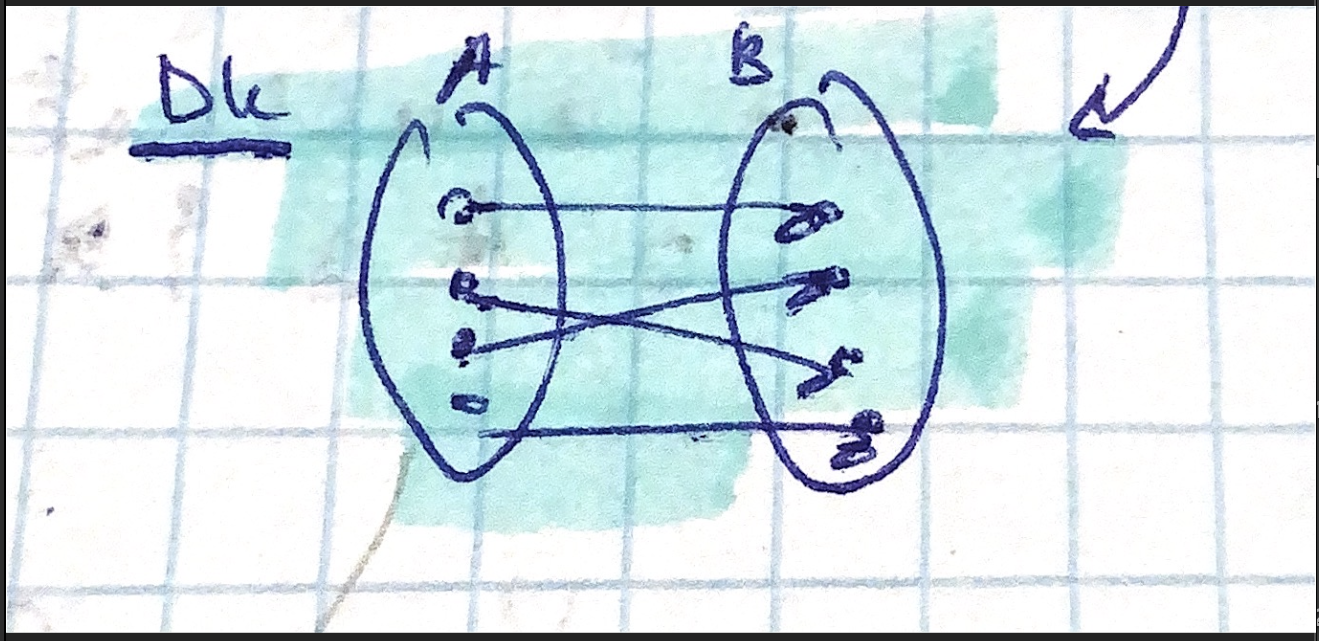
Tvrzení o počtu funkcí

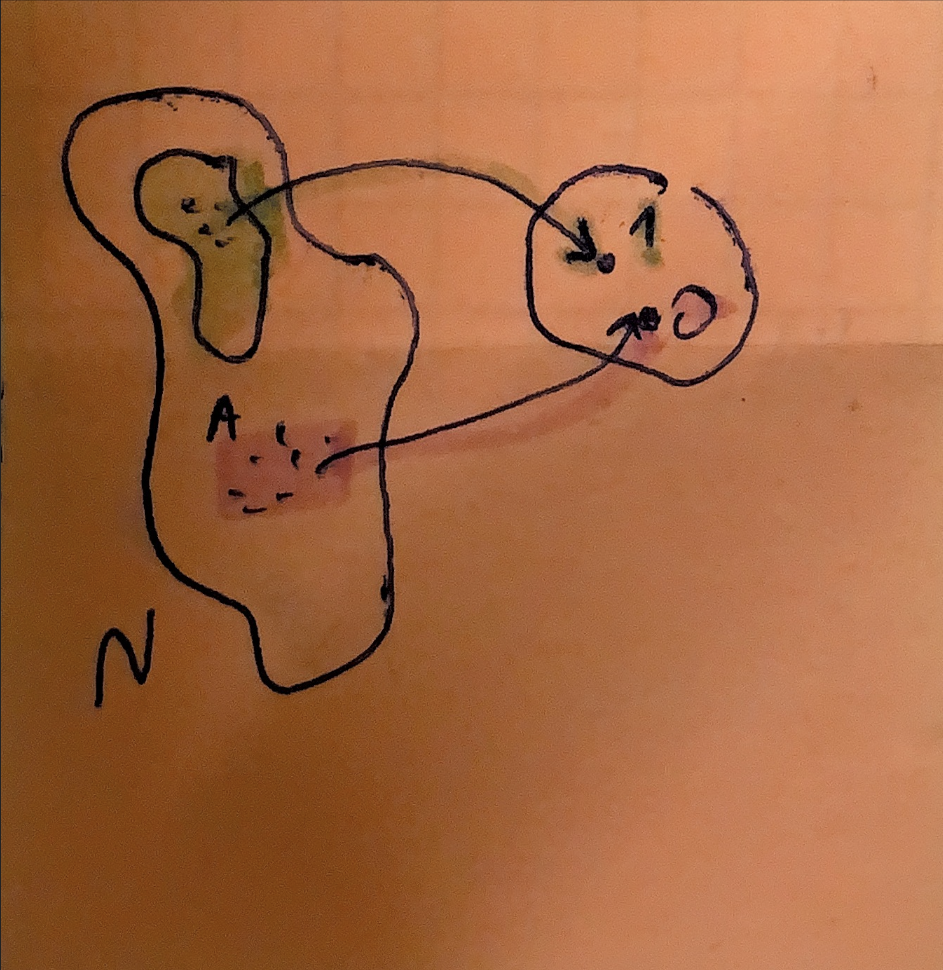
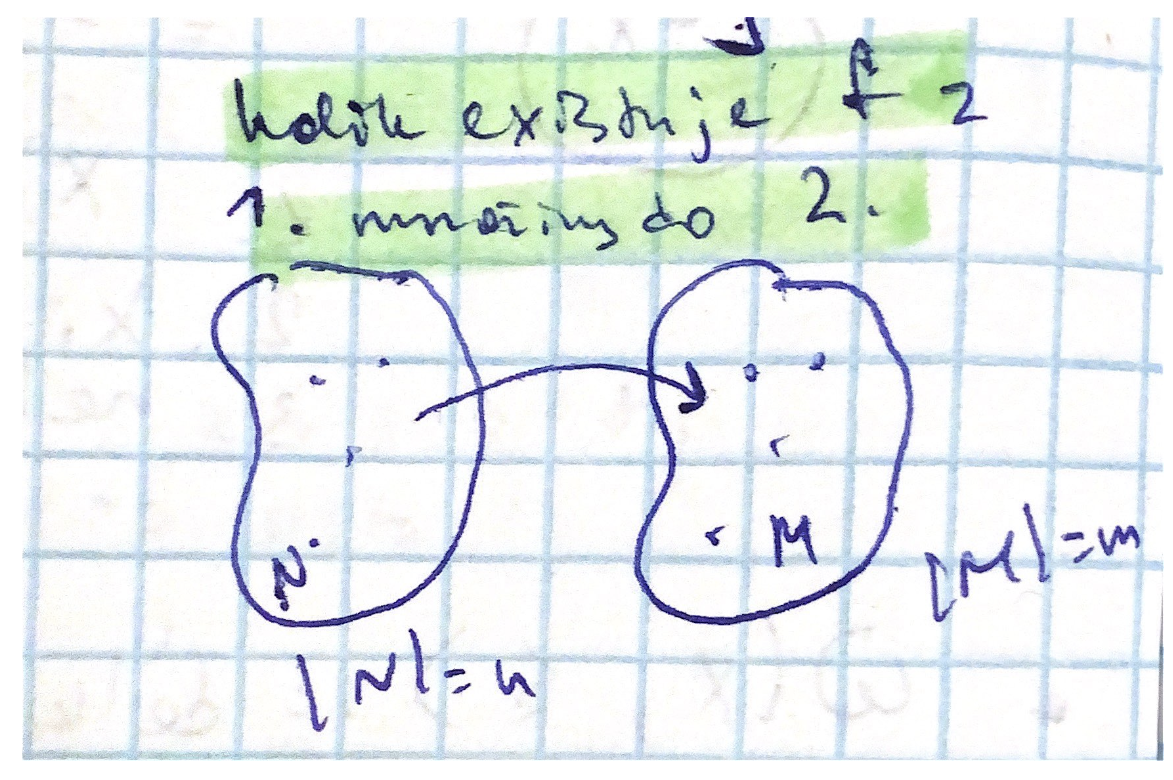
Nechť N je nějaká n-prvková množina, M je m-prvková množina, m≥1, potom počet všech zobrazení (neboli funkcí) f:  N -> M je mⁿ

Důkaz: indukcí (podle n) pro každý prvek x ∈ N máme m různých možností jak definovat f(x). x' != x volba f(x') je nezávislá na volbě f(x)

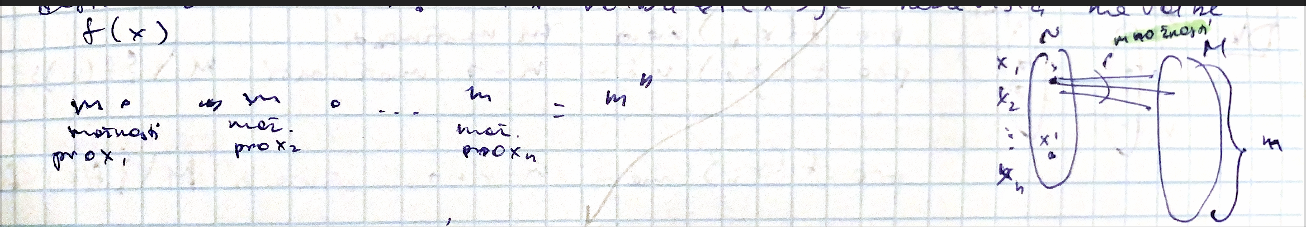
Úvod do kombinatoriky

[n] = {1, 2, ..., n}

n^k = n*(n-1)*...*(n-k+1) - klesající mocnina

n⁰ = 1, jelokož je to prázdný součin

Paskalův trojúhelník

Tvrzení o počtu prostých funkcí

počet prostých funkcí z n-prvkové množiny do m-prvkové množiny: # {f: [n] -> [m] | f prostá} = mⁿ = m*(m-1)*...*(m-n+1)

Důkaz:

pro f(x₁) máme m možností

pro f(x₂) máme m-1 možností (M\f(x₁))

...

pro f(x_n) máme m-n+1 možností (M\{f(x₁), ..., f(x _n-1)})

-> celkem m*(m-1)*...*(m-n+1) = mⁿ

Pár definic

• permutace na n-prvkové množině N je bijekce z N -> N. # permutací N je nⁿ = n*(n-1)*...*(n-n+1) = n!
• neuspořádáná k-tice z N = k-prvková podmnožina N 
• (N nad k) k-prvkové podmnožiny N (N je množina)
• |(N nad k)| = (n nad k) = (n!)/((n-k)!*(k!)), kde n je počet prvků množiny N

Tvrzení o počtu podmnožin

Libovolná n-prvková množina X má právě 2ⁿ podmnožin

Důkaz: podmnožině A ⊆ N přiřádíme její charakteristickou funkci  c_A : N -> {1, 0} a ∈ N c_A(a) = 1 a ∈ A nebo 0 a !∈ A. Mezi funkcemi z N -> {1, 0}  a podmnožinami N je bijekce, tedy: stačí spočítat počet funkcí z N -> {1, 0} (# podmnožin je stejný)

podle tvrzení o počtu funkcí máme, že # funkcí: N -> {1, 0} = 2ⁿ  

Binomická věta

Počet funkcí

• počet funkcí z n-prvkové množiny N do m-prvkové množiny M: #f: N -> M = mⁿ, pro n = |N|, m =|M| (nebo jiný zápis: #f: [n] -> [m] = mⁿ)
• ∀ z n prvků si nezávisle na ostátních múžeme vybrat m možnosti, kam se zobrazí

Některé vlastnosti kombináčních čísel (binomický koeficient)

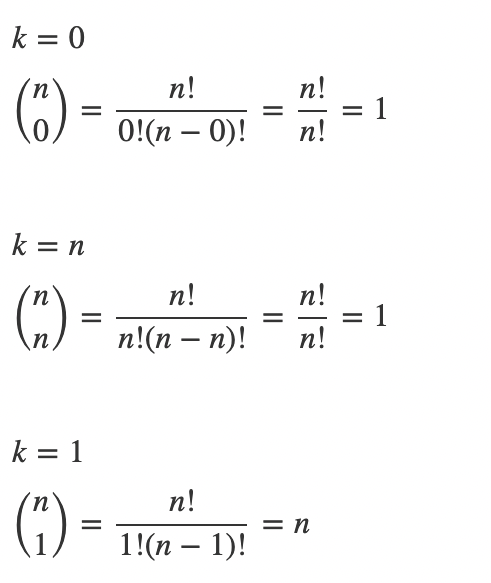
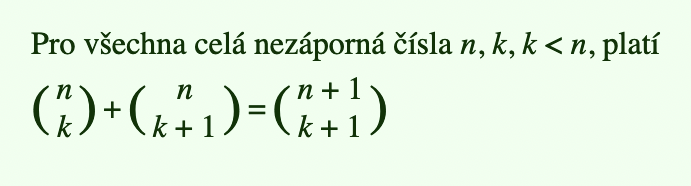
1. existuje právě jedna prázdná množina
2. existuje jeda plná množina
3. existuje n 1-prvkových podmnožin
4. každá (n-k)-prvková množina je určena svými chybějícimi prvky
5. k-prvkových podmnožin n-prvkové množiny je dtejně jako podmnožin s n-k prvky

Tvrzení o počtu k-prvkových podmnožin z n-prvkové množiny

# {A ⊆ N | |A| = k} = n^k/(k!) = (n*(n-1)*...*(n-k+1))/(k!) = (k nad n​) (binomický koeficient)

Důkaz: pomocí počítání 2 způsoby. Počítáme uspořádáné k-tice bez opakování

1. způsob: úspořáadaných k-tic bez opakování je jako prostých funkcí f: N -> [k] ... n^k

2. způsob: vebereme neuspořádananou k-tici ((n nad k) způsobů) a pak k! způsobů jak je uspořádat -> (n nad k)*k!

a proto n^k = (n nad k)*k!/k!

Důkaz 5.????????

Princip sudosti

Pro každý (konečný) graf G platí 

∑_{v∈ V(G)} (G)deg v = 2*|E(G)|

(jelikož každá hrana má dva vrcholy a tuhle hranu započítíáme pro každý y těchto dvou vrcholů)

Trošočku o vzdalenosti v grafu

• d(u, v) ≥ 0
• d(u, v) = 0 <=> u = v
• d(u, v) = d(v, u)
• d(u, v) ≤ d(u, w) + d(w, v)

Malá poznámka o prostém zobrazení

Množinové operace s relacemi ?????

Relace musejí být ze stejné množiny na stejnou.

Spousta definic

vrcholy v₁a v₂ sousedí v G, jestliže v₁v₂ ∈ E(G) (jsou spojené hranou)

vrchol v a hrana e jsou incidentní jestliže v ∈ e (vrchol v je jedním z konců hrany)

psloupnost v₀, e₁, v₁, e₂, ..., e_n, v_n je sled (z v₀ do v_n délky n) jestliže vrcholy  e₁, ..., e_n jsou hrany a e_i je incidentní s v_i-1 a v_i pro i = 1, 2, ..., n

sled je uzavřený, pokud v₀=v_n

Sled je:

• tah, jestliže hrany e₁, ..., e_n jsou navzájem různé (nelze procházet hranami, kterými už šel)
• cesta, jestliže vrcholy v₀, ..., v_n (a tedy i hrany e₁, ..., e_n) jsou navzájem různé (nelze jít i vrcholy, kterými dříve šel)
  
• kružnice, jestliže  jestliže vrcholy v₀, ..., v_n (a tedy i hrany e₁, ..., e_n) jsou navzájem různé a v₀=v_n

Vlastnosti relace R ⊆ X*X

1. Reflexivní: aRa pro každé a∈X (každý bod je v relaci sam se sebou, jinými slovy musí vést šipka z bodu do sebe samého
2. Symetrická: pro každé a a b z X platí, že pokud a je v relaci s b, je i b v relaci s a: aRb => bRa
3. Slaběantisymetrická: platí-li pro všechna a a b z X, že jestliže a je v relaci s b a b je v relaci s a, pak a = b: aRb ^ bRa => a=b
4. Antisymetrická: pro žádné a, b ∈ X neplatí zároveň aRb a bRa
5. Tranzitivní:je-li prvek a v relaci s b a b v relaci s c , pak je a v relaci s c (vede-li šipka z vrcholu a do b a (jiná) šipka z b do c, povede šipka i z a do c)

Příklady relace

1. Relace rovnosti (diagonální relace) na množině M: M={1, 2, 3, 4} R={(1, 1), (2, 2), (3, 3), (4, 4)}
2. xRy, pokud x|y: R={(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (1, 3), (1, 4), (2, 4)}
3. Pokud máme množiny A a B, A*B je univerzální relace
4. Prázdná relace

Ještě více definic

• u ∽ v, pokud mezi u a v existuje cesta ( ∽ je ekvivalence)
• Třídy ekvivalence ∽ jsou zvany komplementy souvislosti G
• Graf je souvislý pokud ∀ u, v ∈ V(G) u ∽ v (jinými slovy ∽ má jenom jednu třídu ekvivalence) (ještě jinými slovy to znamená, že z každého vrcholu lze dojít do jakehokoliv jiného vrcholu po hranách v tomto grafu)
  
• Vzdalenost v grafu: d(u, v) je délka nekratší cesty mezi u a v (pokud u !∽ v, tak d(u, v) = ∞
  
• Stupeň vrcholu v je deg(v) = počet hran incidentních s vrcholem v
  
• Bipartitní graf G: ∃ rozklad množiny V(G) na parity X, Y, t.ž. E(G) ⊆ {{x; y} | x ∈ X, y ∈ Y} (jnými slovy vrcholy grafu jde rozdělit na dvě skupiny tak, že vrcholy z jedné skupiny nebudou sousedit)
  

Druhy funkce

• prostá funkce (injektivní), jestliže pro x != y je f(x) != f(y): vchází do jednoho bodu nejvýš jedna šipka
• funkce na (surjektivní), jestliže pro každé y ∈ Y existuje x ∈ X splňující f(x)=y: vchází do jednoho bodu aspoň jedna šipka
• vzájemně jednoznačná funkce (bijektivní), jestliže f je prostá a na: vchází do každého bodu právě jedna šipka

Funkce

• Funkce z množiny X do množiny Y je relace f ⊆ XxY, splňující dodatečnou podmínku, že pro každý prvek x ⊆ X existuje právě jediný prvek y ⊆ Y tak, že xfy
• Značení: f(x), xfy, f: X → Y funkce z množiny X do množiny Y

Poznámky

• Pokud máme množiny A a B, A*B je univerzální relace
• ∅ je také podmnožinou kartezského součinu

Skladání funkce

• Jsou-li f: X → Y  a g: Y → Z funkce, potom můžeme definovat novou funkci h: X → Z předpisem: h(x) = g(f(x)), pro každé x  ∈  X

Poznamka: 

funkce: h(x) = g(f(x))

relace: g•f: X → Z

Příklady funkce

• sin: R → [-1, 1]
• sgn: R → {-1, 0, 1}
• f(a, b) ∈ Y, pro a ∈ A, b ∈ B
• f(x) = x je identita, diagonální relace

Důkazové techniky

1. Indukce 

2. Sporem 

3. Přímý 

4. 

Podgraf

• graf H je podgrafem G, jestliže V (H) ⊆ V (G) a E(H) ⊆ E(G) ∩ (V(H) nad 2) ??(jak napsat kombinacni cislo)
• graf H je indukovaný podgraf G, jestliže V(H) ⊆  V(G) a E(H) = E(G)∩ (V(H) nad 2) ( taky značíme G[V(H)] a říkáme, že je indukovaný vrcholy V(H)
• Doplňek grafu G je graf se stejnými vrcholy jako v grafu G, ale má všechny šipky kromě těch, které má původní graf G (je jakoby dopněním do úplného grafu) 

Věta

Relace R

• Množina uspořádaných dvojic. Jsou-li X a Y množiny, nazývá se libovolná podmnožina kartezského součinu X * Y relací mezi X a Y.
• X=Y, pak jde o relaci na X, což je libovolná podmnožina R ⊆ X²
• Značení: xRy, (x, y) ∈ R

Kartezský součin X*Y

• Kartezský součin: X * Y: množina všech uspořádaných dvojic tvaru (x, y), kde x ∈ X, y ∈ Y
• X * Y = {(x, y); x ∈ X, y ∈ Y}
• X=Y=R, tak X*Y jsou všechny body v rovině
• Může být i X³ = X*X*X (x, y, z)

neuspořádaná/uspořádaná dvojice

• neuspořádaná dvojice: {x, y} = {y, x}, je-li x=y, pak {x, y} je jednoprvková množina
• uspořádaná dvojice: (x, y) != (y, x) (záleží na pořádí)

Graf

• je uspořádaná dvojice (V, E), kde V je množina vrcholů a E je množina dvoubodových podmnožin (hran) množiny V
• značení: G = (V, E), |V| = n, |E|  = m
• množina vrcholů V(G), hran E(G)

počet různých grafů???????

Izomorfismus

• Dva grafy jsou izomorfní, jestliže existuje bijekce f: V(G₁) -> V(G₂) t.ž. uv ∈ E(G₁) <=> f(u)f(v) ∈ E(G₂) (jinými slovy G₁ a G₂ se líší jenom pojmenováním vrcholů)
• Značení: G₁ ⋍ G₂
• Relace izomorfismu je ekvivalence (podle ověření vlastností ekvivalence)

Oerace na relacích

• Inverze: pro relaci R mezi X a Y je R^-1={(y, x): (x, y) náleží R} (šipka vede odtud, kam vedla dříve).
• Skládání: pro relaci R₁ mezi X a Z a relaci R_2 mezi Z a Y je R₁•R₂ = {(x, y) : (existuje z) (x, z) náleží R₁ ^ (z, y) náleží R₂} relace mezi X a Y. ( x bude v relaci s z, když bude existovat jakoby můstek vztahu s jiným prvkem, šipka vede od x k nějakému z a pak od tohoto z do y. Stejně to může být i pro více než dvě relace)
• Skládání relace není komutativní: R₁•R₂ != R₂•R₁

Tvrzení

Nechť f: X → Y a g: Y → Z  jsou funkce

• Jsou-li f, g prosté, je g•f funkce prostá
  
• Jsou-li f, g na, je g•f funkce na
• Jsou-li f, g vzájemně jednoznačné, je g•f funkce vzájemně jednoznačná
  
• Pro každou funkci f: X → Y existuje množina Z, prostá funkce h: X → Z  tak, že f = h•g (každou funkci lze napsat jako složení funkce prosté a funkce na)

Každá neprázdná konečná ČUM má aspoň jeden minimální prvek.

DŮKAZ

↓ pro částečné uspořádání

• Pro částešné uspořádání ≼ na množině X definujme ↓ ≼ x = {y : y ∈X, y ≺x}
• Necht’  je částečné uspořádání na množině X a x, y ∈ X. Pak x ≼ y právě když ↓ ≼ x ⊆ ↓ ≼ y. Navíc, jestliže x  != y, pak ↓ ≼ x != ↓ ≼ y

Porovnatelnost v ČUM

• Porovnatelné prvky v částečném uspořádání ≼ jsou ty, pro které platí: x ≼ y nebo y ≼ x, a tvoří řetězec 
• Neporovnatelné prvky jsou ty, pro které platí: x !≼ y a y !≼ x, a tvoří spolu antiřetězec. Jinými slovy, antiřetězec je množina navzájem neporovnatelných prvků.
• Příklad: relace ” x dělí y“ je uspořádáním na N. Pro n=9, kde n je [n], řetězec je {1, 2, 4, 8} a antiřetězec je {5, 7, 9, 8, 6}

Typy relace

• Ekvivalence: relace R na množině X je ekvivalence pokud R je reflexivní, symetrická a tranzitivní
• Částečné uspořádání: pokud R je reflexivní, slabě antisymetrická a tranzitivní.
• Ostré částečné uspořádání: R je antisymetrická a tranzitivní. ( rozdíl mezi ostrým a obyčejným ču spočívá v tom, že pro obyčejné může být relace <= (nebo =>) a pro ostré musí být jenom < (>), tím je vyloučena reflexivita)

Příklady

Úplný graf na n vrcholech K_n: n >= 1 a každá dvojice je spojena hranou ( V (K_n) = {v₁, . . . , v_n} a E(K_n) = {v_iv_j : 1 ≤ i < j ≤ n})

Cesta na n vrcholech P_n: P_n = ([n], {{1, 2}, {2, 3}, ..., {n-1, n}}) (vrcholů je o 1 navíc než hran)

Kružnice (cyklus) C_n na n vrcholech n >= 3: C_n = ([n], {{1, 2}, {2, 3}, ..., {n-1, n}, {n, 1}}) (poslední vrchol je spojen nejen s předposledním ale i s prvním)

Prázdný graf E_n: V(E_n) = {1, ..., n}, E(E_n) = ∅   (nemá hrany)

Orientovany graf: je dvojice G = (V, E), t.ž. V je množina vrcholů a E ⊆  V*V, t.j. hrany jsou šipky

Množiny

Základní množiny čísel:
1. N: přírozená čísla
2. Z: celá čísla
3. R: realná čísla
4. Q: racionální čísla
5. C: Komplexní čísla

• 2^A = P(A) - množina všech podmnožin nějaké množiny, potenční množina (všechny možné podmnožiny, začinaje prázdnou množinou až do množiny obsahující všechny prvky vychozí množiny)

Oerace s množinami:
1. Sjednocení:  A ⋃ B = {x | x ∈ A ∨ x ∈ B}
2. Průnik: A ⋂ B = {x | x ∈ A ∧ x ∈ B}

3. Rozdíl: A\B = {x ∈ A| x ∈/ B}
4. Doplněk: A' - všechny prvky, které nejsou v množině A

Spousta definic

• a a b jsou neporovnatelné , pokud a !≼ b a b !≼ a
• S ⊆ X je antiřetězec, pokud ∀ a, b ∈ S: a a b jsou neporovnatelné
• S ⊆ X je řetězec, pokud ∀ a, b ∈ S  a ≼ b nebo b ≼ a
• a ∈  X  je nejmenší, pokud ∀  b ∈ X:  a ≼ b
• a ∈  X  je minimální, pokud ∄ b ∈ X:  b ≼ a
• a ∈  X  je největší, pokud ∀  b ∈ X:  b ≼ a
• a ∈  X  je maximální, pokud ∄ b ∈ X:  a ≼ b

Podrobněji o částečném uspořádání

• Uspořádáná množina je dvojice (X, R), kde X je množina a R je uspořádání na X.

Značení:

• a ≼ b, a pod b / a menší než  b
• a ≺ b, pokud a ≼ b ∧ a != b, a ostře pod b
• a ⋟ b <=> b ⋞ a: obracená nerovnost

Částečně uspořádaná množina - ČUM

Tvrzení o třídách ekvivalence

Nechť R je ekvivalence, potom 

1. Pro každé a ∈ X platí a ∈ R[a]: třída nemůže být prázdná, jelikož sám prvek, který třídu určuje je v této třídě
2. Jestliže a, b ∈ X a aRb, pak R[a] = R[b]: jestli se dva prvky jsou v relaci, pak jejich třídy jsou stejné.
3. Třídy ekvivalence jednoznačně určují (popisují) relaci R: třídy ekvivalence jsou disjunktní (jinými slovy nemají společené prvky, a pokud mají, tak to jsou stejná třída), ale každý prvek spadá do nějaké třídy, což znamená, že společně třídy určují relaci R

Třídy ekvivalence

• nechť R je ekvivalence na množině X. Třída ekvivalence prvku a náleží X R[a] = {x: x náleží X, aRx}
• Třídu ekvivalence může reprezentovat jakýkoliv prvek, náležející této třídě

Ekvivalentní prvky - prvky, které jsou ve stejné třídě

Každé lineární uspořádání je částečné uspořádání

Lineární uspořádání

(úplné):  ≼ je úplné uspořádání pokud ∀ a, b ∈ X  a ≼ b ∨ b ≼ a

Příklad:

• ( N, ≤ )
• inkluze množin
• lexikografické uspořádání: ( A, ≤ ) lineární uspořádaná množina (abeceda) (pro X = {a, ... , z} (c, d) ≤ (e, a))

????????

Hasseův diagram

obrázek, kde prvky x jsou body, z a do b vede šipka nahoru, pokud a ≼ b a zároveň neexistuje c: a ≼ b ≼ c (c != a, b)

1. nekreslíme prvky, které jsou ve vztahu sam se sebou (bez šipek označujících reflexivitu)
2. nekreslíme prostředního předchůdce
3. od nejmenšího k většímu 

Hasseův diagram pro P({x, y, z})

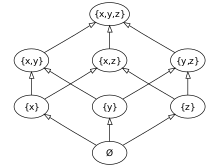
Bezprostřední předchůdce (BP)

Nechť (X, ≼) je uspořádaná množina. Řekneme, že prvek x je bezprostřední předchůdcem prvku y, pokud platí: 

• x ≺ y
• neexistuje žádné t ∈ X takové, že x ≺ t ≺ y

Příklad: pro ( N, < ) 5 je BP prvku 6, ale 3 není BP 5, protože mezi nimi je 4

Ostré uspořádání

Pokud tato relace je ⊂

• ireflexivní (antireflexivní):  ¬ (a ⊂ a)
• slabě antisymetrická: (a ⊂ b) ⇒ ¬ (b ⊂ a)
• tranzitivní: a ⊂ b ∧ b ⊂ c ⇒ a ⊂ c

Jediný rozdíl spočívá v tom, že teď a nemůže být v relaci samo se sebou ∀ a ∈ X (množina, na které je relace)

Kombinatorické počítání

Značení

• [n] := {1, . . . , n}
• n^k := n ·(n −1) ·. . . ·(n −k + 1) (klesající mocnina)
• n⁰ = 1, (prázdný součin)

Počet funkcí