Lineární algebra
Created by Ema Tomanová

Hodnost matice
Hodnost matice (též Rank) je definována jako dimenze lineárního obalu souboru řádků matice. Je to číslo, které představuje počet nezávislých řádků nebo sloupců matice.
Pro matici A{\displaystyle \mathbf {A} } typu m×n{\displaystyle m\times n}
typu m×n{\displaystyle m\times n} platí
platí
h(A)≤min{m,n}{\displaystyle h(\mathbf {A} )\leq \min\{m,n\}} ,
,
kde min{m,n}{\displaystyle \min\{m,n\}\,} představuje nejmenší hodnotu z množiny {m,n}{\displaystyle \{m,n\}\,}
představuje nejmenší hodnotu z množiny {m,n}{\displaystyle \{m,n\}\,} . Hodnost matice typu m×n{\displaystyle m\times n}
. Hodnost matice typu m×n{\displaystyle m\times n} je tedy menší nebo rovna menšímu z čísel m,n{\displaystyle m,n}
je tedy menší nebo rovna menšímu z čísel m,n{\displaystyle m,n} .
.
Hodnost
Regulární
Regulární matice (v některé literatuře též invertibilní) je taková čtvercová matice, jejíž determinant je různý od nuly, tzn.
detA≠0{\displaystyle \det \mathbf {A} \neq 0}
Ekvivalentně lze též tvrdit:
- Její řádky jsou lineárně nezávislé.
- Její sloupce jsou lineárně nezávislé.
- Hodnost čtvercové regulární matice o velikosti n×n je právě n.
- Existuje k ní inverzní matice.
- Všechna její vlastní čísla jsou nenulová.
Opakem regulární matice je tzv. singulární matice s nulovým determinantem.
Diagonální
V lineární algebře označuje pojem diagonální matice čtvercovou matici n×n, která může mít nenulové prvky pouze na hlavní diagonále. Někdy se tento termín používá i pro obdélníkové matice, ale v tomto článku toto zobecnění nebudeme uvažovat.
Příkladem diagonální matice je matice
(10004000−3){\displaystyle {\begin{pmatrix}1&0&0\\0&4&0\\0&0&-3\end{pmatrix}}}
Diagonální matice se někdy zapisuje jako diag(a1, …, an), kde ai odpovídá prvku matice aii. Matice v předchozím příkladu je tedy diag(1, 4, -3).
Každá jednotková matice a každá čtvercová nulová matice je diagonální maticí.
Singulární
Singulární matice je taková čtvercová matice, jejíž determinant je roven nule, tzn.
detA=0{\displaystyle \det \mathbf {A} =0}
Ekvivalentně lze též tvrdit:
- Její řádky jsou lineárně závislé.
- Její sloupce jsou lineárně závislé.
- Hodnost čtvercové singulární matice o velikosti n×n je menší než n.
- Neexistuje k ní inverzní matice.
Opakem singulární matice je tzv. regulární matice s nenulovým determinantem.
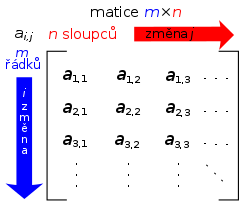
Matice
Matice je obdélníkové či čtvercové schéma čísel nebo nějakých matematických objektů – prvků matice (též elementů matice). Obsahuje obecně m řádků a n sloupců. Hovoříme pak o matici typu m×n{\displaystyle \scriptstyle m\times n
Hodnost transpozice
Hodnost matice a transpozice:
Pro libovolnou matici A∈Rm×n platí
rank(A) = rank(AT)
Jednotková
V lineární algebře označuje pojem jednotková matice velikosti n čtvercovou matici n×n{\displaystyle n\times n} , která má na hlavní diagonále jedničky a na ostatních místech nuly. Jednotková matice se značí In, případně jen I, je-li velikost nepodstatná nebo lze-li ji odvodit z kontextu
, která má na hlavní diagonále jedničky a na ostatních místech nuly. Jednotková matice se značí In, případně jen I, je-li velikost nepodstatná nebo lze-li ji odvodit z kontextu
I1=[1], I2=[1001], I3=[100010001], ⋯, In=[10⋯001⋯0⋮⋮⋱⋮00⋯1]{\displaystyle I_{1}={\begin{bmatrix}1\end{bmatrix}},\ I_{2}={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\ I_{3}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},\ \cdots ,\ I_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}}
Důležitou vlastností In je
AIn = A a InB = B
Typy matic
Inverzní matice
Inverzní matice k dané regulární matici je taková matice, která po vynásobení s původní maticí dá jednotkovou matici. Inverzní matici k matici A značíme A−1.
Vynásobením regulární matice s její inverzí dostáváme jednotkovou matici.
A⋅A−1=A−1⋅A=1,{\displaystyle \mathbf {A} \cdot \mathbf {A} ^{-1}=\mathbf {A} ^{-1}\cdot \mathbf {A} =\mathbf {1} ,}
kde 1 je jednotková matice.
Inverzní matici lze sestrojit pouze pro regulární matici – čtvercovou matici jejíž determinant není roven nule.
Inverze
Trojúhelníková
Matici, která má všechny prvky pod hlavní diagonálou nulové, označujeme jako horní trojúhelníkovou matici. Taková matice má tvar
(a11a12⋯a1n0a22⋯a2n⋮⋮⋱⋮00⋯ann){\displaystyle {\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\0&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{pmatrix}}}
Podobně označujeme jako dolní trojúhelníkovou matici takovou matici, která má všechny prvky nad diagonálou nulové.
Transpozice
Matici, která vznikne z matice A{\displaystyle \mathbf {A} } vzájemnou výměnou řádků a sloupců, označujeme jako transponovanou matici a značíme AT{\displaystyle \mathbf {A} ^{T}}
vzájemnou výměnou řádků a sloupců, označujeme jako transponovanou matici a značíme AT{\displaystyle \mathbf {A} ^{T}} . Pro jednotlivé prvky transponované matice platí
. Pro jednotlivé prvky transponované matice platí
aijT=aji{\displaystyle a_{ij}^{T}=a_{ji}\,} .
.
Pokud má matice A{\displaystyle \mathbf {A} } rozměry (m,n){\displaystyle (m,n)}
rozměry (m,n){\displaystyle (m,n)} , pak její transpozicí vznikne matice o rozměrech (n,m){\displaystyle (n,m)}
, pak její transpozicí vznikne matice o rozměrech (n,m){\displaystyle (n,m)} .
.
Vlastnosti transpozice
Dvojitou transpozicí získáváme zpět původní matici:
(AT)T=A{\displaystyle \left(\mathbf {A} ^{\mathrm {T} }\right)^{\mathrm {T} }=\mathbf {A} \quad \,} .
.
Násobení skalárem se dá vytknout před operaci transpozice:
(cA)T=cAT{\displaystyle (c\mathbf {A} )^{\mathrm {T} }=c\mathbf {A} ^{\mathrm {T} }\,}
Transpozice součtu matic je součtem transponovaných matic:
(A+B)T=AT+BT{\displaystyle (\mathbf {A} +\mathbf {B} )^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }\,}
Transpozice součinu dvou matic je součinem transponovaných matic v obráceném pořadí:
(AB)T=BTAT{\displaystyle \left(\mathbf {AB} \right)^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }\,}
Transpozice inverzní matice je rovna inverzi transponované matice:
(AT)−1=(A−1)T{\displaystyle \left(\mathbf {A} ^{\mathrm {T} }\right)^{\mathrm {-1} }=\left(\mathbf {A} ^{\mathrm {-1} }\right)^{\mathrm {T} }\,}
Skládání zobrazení
Složené zobrazení z lineárních zobrazení je opět lineární. Přesněji, nechť A∈L(X,Y){\displaystyle \scriptstyle A\in {\mathcal {L}}(X,Y)} a B∈L(Y,Z){\displaystyle \scriptstyle B\in {\mathcal {L}}(Y,Z)}
a B∈L(Y,Z){\displaystyle \scriptstyle B\in {\mathcal {L}}(Y,Z)} . Pak složené zobrazení BA definované vztahem
. Pak složené zobrazení BA definované vztahem
(BA)(x→)=B(A(x→)){\displaystyle (BA)({\vec {x}})=B(A({\vec {x}}))}
pro všechna x→∈X{\displaystyle \scriptstyle {\vec {x}}\in X} je lineární, tj. BA∈L(X,Z){\displaystyle \scriptstyle BA\in {\mathcal {L}}(X,Z)}
je lineární, tj. BA∈L(X,Z){\displaystyle \scriptstyle BA\in {\mathcal {L}}(X,Z)} .
.
Důkaz: Vezměme libovolné α∈T{\displaystyle \scriptstyle \alpha \in \mathbb {T} } a libovolné vektory x→,y→∈X{\displaystyle \scriptstyle {\vec {x}},{\vec {y}}\in X}
a libovolné vektory x→,y→∈X{\displaystyle \scriptstyle {\vec {x}},{\vec {y}}\in X} . Pak (BA)(αx→+y→)=B(αA(x→)+A(y→))=αB(A(x→))+B(A(y→))=α(BA)(x→)+(BA)(y→){\displaystyle \scriptstyle (BA)(\alpha {\vec {x}}+{\vec {y}})=B(\alpha A({\vec {x}})+A({\vec {y}}))=\alpha B(A({\vec {x}}))+B(A({\vec {y}}))=\alpha (BA)({\vec {x}})+(BA)({\vec {y}})}
. Pak (BA)(αx→+y→)=B(αA(x→)+A(y→))=αB(A(x→))+B(A(y→))=α(BA)(x→)+(BA)(y→){\displaystyle \scriptstyle (BA)(\alpha {\vec {x}}+{\vec {y}})=B(\alpha A({\vec {x}})+A({\vec {y}}))=\alpha B(A({\vec {x}}))+B(A({\vec {y}}))=\alpha (BA)({\vec {x}})+(BA)({\vec {y}})} , což je ekvivalentní linearitě složeného zobrazení.
, což je ekvivalentní linearitě složeného zobrazení.
Lineární zobrazení
Nechť X a Y jsou vektorové prostory nad týmž tělesem T{\displaystyle \scriptstyle \mathbb {T} } . Zobrazení L{\displaystyle \scriptstyle L}
. Zobrazení L{\displaystyle \scriptstyle L} z prostoru X do prostoru Y, tj. L:X→Y{\displaystyle \scriptstyle L:X\to Y}
z prostoru X do prostoru Y, tj. L:X→Y{\displaystyle \scriptstyle L:X\to Y} , se nazývá lineární zobrazení, právě když pro libovolné vektory x→,y→∈X{\displaystyle \scriptstyle {\vec {x}},{\vec {y}}\in X}
, se nazývá lineární zobrazení, právě když pro libovolné vektory x→,y→∈X{\displaystyle \scriptstyle {\vec {x}},{\vec {y}}\in X} a pro libovolný prvek α{\displaystyle \scriptstyle \alpha }
a pro libovolný prvek α{\displaystyle \scriptstyle \alpha } z tělesa T{\displaystyle \scriptstyle \mathbb {T} }
z tělesa T{\displaystyle \scriptstyle \mathbb {T} } toto zobrazení splňuje následující dvě podmínky:
toto zobrazení splňuje následující dvě podmínky:
- aditivita: L(x→+y→)=L(x→)+L(y→){\displaystyle L({\vec {x}}+{\vec {y}})=L({\vec {x}})+L({\vec {y}})}
 ,
, - homogenita: L(αx→)=αL(x→){\displaystyle L(\alpha {\vec {x}})=\alpha L({\vec {x}})}
 .
.
Obraz vektoru x→∈X{\displaystyle \scriptstyle {\vec {x}}\in X} při lineárním zobrazení L{\displaystyle \scriptstyle L}
při lineárním zobrazení L{\displaystyle \scriptstyle L} se značí L(x→){\displaystyle \scriptstyle L({\vec {x}})}
se značí L(x→){\displaystyle \scriptstyle L({\vec {x}})} . Často se ale pro jednoduchost závorky vypouští a píše se jen Lx→{\displaystyle \scriptstyle L{\vec {x}}}
. Často se ale pro jednoduchost závorky vypouští a píše se jen Lx→{\displaystyle \scriptstyle L{\vec {x}}} . Podobně obraz množiny P⊂X{\displaystyle \scriptstyle P\subset X}
. Podobně obraz množiny P⊂X{\displaystyle \scriptstyle P\subset X} se značí L(P){\displaystyle \scriptstyle L(P)}
se značí L(P){\displaystyle \scriptstyle L(P)} .
.
Lineární struktura zobrazení i vektorového prostoru, na kterém je definováno, umožňuje velmi zjednodušit zápis, jakým toto zobrazení působí na libovolný vektor. Tato vlastnost tím spíše vyplyne na konečněrozměrných prostorech. Pro konkrétnost mějme vektorový prostor Xn{\displaystyle \scriptstyle X_{n}} konečné dimenze n. Existuje v něm tedy n-členná báze x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}}
konečné dimenze n. Existuje v něm tedy n-členná báze x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}} a každý vektor x→{\displaystyle \scriptstyle {\vec {x}}}
a každý vektor x→{\displaystyle \scriptstyle {\vec {x}}} tohoto prostoru lze vyjádřit jako vhodnou lineární kombinaci x→=∑i=1nαix→i{\displaystyle \scriptstyle {\vec {x}}=\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}}
tohoto prostoru lze vyjádřit jako vhodnou lineární kombinaci x→=∑i=1nαix→i{\displaystyle \scriptstyle {\vec {x}}=\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}} . Využijeme-li nyní linearity zobrazení A, dostáváme
. Využijeme-li nyní linearity zobrazení A, dostáváme
y→=A(x→)=A(∑i=1nαix→i)=∑i=1nαiA(x→i).{\displaystyle {\vec {y}}=A({\vec {x}})=A\left(\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}\right)=\sum _{i=1}^{n}\alpha _{i}A({\vec {x}}_{i}).}
Obraz každého vektoru y→{\displaystyle \scriptstyle {\vec {y}}} lze tedy vyjádřit jako nějakou lineární kombinaci vektorů A(x→i){\displaystyle \scriptstyle A({\vec {x}}_{i})}
lze tedy vyjádřit jako nějakou lineární kombinaci vektorů A(x→i){\displaystyle \scriptstyle A({\vec {x}}_{i})} , kde koeficienty jsou totožné s koeficienty u vzoru x→{\displaystyle \scriptstyle {\vec {x}}}
, kde koeficienty jsou totožné s koeficienty u vzoru x→{\displaystyle \scriptstyle {\vec {x}}} . Celou informaci o struktuře zobrazení A lze tak získat pouze ze znalosti toho, jak působí na bazické vektory. Rozvinutím právě uvedené myšlenky pak dospíváme k definici matice lineárního zobrazení, jak je uvedeno níže.
. Celou informaci o struktuře zobrazení A lze tak získat pouze ze znalosti toho, jak působí na bazické vektory. Rozvinutím právě uvedené myšlenky pak dospíváme k definici matice lineárního zobrazení, jak je uvedeno níže.
Jádro
Jako jádro matice A nebo také nulový prostor matice A se nazývá množina všech řešení homogenní soustavy lineárních rovnic Ax=o. Označujeme se Ker A.
Pozorování 1: Jsou-li u a w dvě řešení soustavy lineárních rovnic Ax = b, pak w - u je řešením soustavy Ax = o.
Pozorování 2: Je-li u řešením soustavy Ax = b a v řešení příslušně homogení soustavy Ax = o, pak u + v je také řešením soustavy Ax = b.
Věta: Je-li u jedno pevně zvolené partikulární řešení soustavy lineárních rovnic Ax=b nad tělesem T, pak se množina všech řešení této soustavy rovná {u+v : v ∈ Ker A} = u + Ker A.
Důkaz: Je-li w řešení soustavy Ax=b, pak (w - u) ∈ Ker A (podle pozorování 1) a tedy w = u + (w - u) ∈ {u + v : v ∈ Ker A}. Naopak pro libovolné v ∈ Ker A je u + v řešením soustavy Ax=b (podle pozorování 2).
Jádro lineárního zobrazení
Jádro lineárního zobrazení A je taková podmnožina definičního oboru A, kterou A zobrazuje na nulový vektor. Jádro zobrazení A značíme symbolem kerA{\displaystyle \scriptstyle \ker A} (jedná se o zkratku ze slova kernel, anglického označení pro jádro). Přesněji: Mějme dva vektorové prostory X a Y nad stejným tělesem T{\displaystyle \scriptstyle \mathbb {T} }
(jedná se o zkratku ze slova kernel, anglického označení pro jádro). Přesněji: Mějme dva vektorové prostory X a Y nad stejným tělesem T{\displaystyle \scriptstyle \mathbb {T} } . Dále nechť A je lineární zobrazení z X do Y, tj.A∈L(X,Y){\displaystyle \scriptstyle A\in {\mathcal {L}}(X,Y)}
. Dále nechť A je lineární zobrazení z X do Y, tj.A∈L(X,Y){\displaystyle \scriptstyle A\in {\mathcal {L}}(X,Y)} . Pak jádro zobrazení A je množina
. Pak jádro zobrazení A je množina
kerA={x→∈X|A(x→)=0→Y},{\displaystyle \ker A=\{{\vec {x}}\in X|A({\vec {x}})={\vec {0}}_{Y}\},}
kde 0→Y{\displaystyle \scriptstyle {\vec {0}}_{Y}} označuje nulový vektor v prostoru Y. Dimenze jádra zobrazení A, tj. dimkerA{\displaystyle \scriptstyle \dim \ker A}
označuje nulový vektor v prostoru Y. Dimenze jádra zobrazení A, tj. dimkerA{\displaystyle \scriptstyle \dim \ker A} , se občas označuje jako defekt zobrazení A. Z vlastností v oddíle Nulový vektor je vidět, že nulový vektor leží v jádře každého lineárního zobrazení. Dokonce lze dokázat následující tvrzení: Lineární zobrazení je prosté právě tehdy, když v jeho jádru leží pouze nulový vektor (důkaz viz Prostota zobrazení). Neboť množina {0→Y}{\displaystyle \scriptstyle \{{\vec {0}}_{Y}\}}
, se občas označuje jako defekt zobrazení A. Z vlastností v oddíle Nulový vektor je vidět, že nulový vektor leží v jádře každého lineárního zobrazení. Dokonce lze dokázat následující tvrzení: Lineární zobrazení je prosté právě tehdy, když v jeho jádru leží pouze nulový vektor (důkaz viz Prostota zobrazení). Neboť množina {0→Y}{\displaystyle \scriptstyle \{{\vec {0}}_{Y}\}} je také vektorový (pod)prostor, tak lze využít tvrzení z oddílu Obrazy a vzory vektorů a jejich podprostorů o vzoru podprostoru abychom uviděli, že jádro zobrazení je vektorový podprostor, tj.
je také vektorový (pod)prostor, tak lze využít tvrzení z oddílu Obrazy a vzory vektorů a jejich podprostorů o vzoru podprostoru abychom uviděli, že jádro zobrazení je vektorový podprostor, tj.
(∀A∈L(X,Y))(kerA⊂⊂X).{\displaystyle (\forall A\in {\mathcal {L}}(X,Y))(\ker A\subset \subset X).}
Inverzní zobrazení
- nverze k lineárnímu zobrazení je opět lineární zobrazení. Přesněji, nechť je A∈L(X,Y){\displaystyle \scriptstyle A\,\in {\mathcal {L}}(X,Y)}
 izomorfní zobrazení (tj. lineární bijekce definovaná na celém X), pak existuje inverzní zobrazení A−1{\displaystyle \scriptstyle A^{-1}}
izomorfní zobrazení (tj. lineární bijekce definovaná na celém X), pak existuje inverzní zobrazení A−1{\displaystyle \scriptstyle A^{-1}} , které je též izomorfní.
, které je též izomorfní.
Důkaz: Neboť je z předpokladů A bijekce, tak určitě existuje její inverze A−1{\displaystyle \scriptstyle A^{-1}} , zbývá ověřit její linearitu. Označme si x→=A−1(u→){\displaystyle \scriptstyle {\vec {x}}=A^{-1}({\vec {u}})}
, zbývá ověřit její linearitu. Označme si x→=A−1(u→){\displaystyle \scriptstyle {\vec {x}}=A^{-1}({\vec {u}})} , y→=A−1(v→){\displaystyle \scriptstyle {\vec {y}}=A^{-1}({\vec {v}})}
, y→=A−1(v→){\displaystyle \scriptstyle {\vec {y}}=A^{-1}({\vec {v}})} , kde vektory u→,v→∈Y{\displaystyle \scriptstyle {\vec {u}},{\vec {v}}\in Y}
, kde vektory u→,v→∈Y{\displaystyle \scriptstyle {\vec {u}},{\vec {v}}\in Y} jsme si vybrali libovolně. Z linearity zobrazení A plyne A(αx→+y→)=αA(x→)+A(y→)=αu→+v→{\displaystyle \scriptstyle A(\alpha {\vec {x}}+{\vec {y}})=\alpha A({\vec {x}})+A({\vec {y}})=\alpha {\vec {u}}+{\vec {v}}}
jsme si vybrali libovolně. Z linearity zobrazení A plyne A(αx→+y→)=αA(x→)+A(y→)=αu→+v→{\displaystyle \scriptstyle A(\alpha {\vec {x}}+{\vec {y}})=\alpha A({\vec {x}})+A({\vec {y}})=\alpha {\vec {u}}+{\vec {v}}} . Zobrazení A tedy vektoru αx→+y→{\displaystyle \scriptstyle \alpha {\vec {x}}+{\vec {y}}}
. Zobrazení A tedy vektoru αx→+y→{\displaystyle \scriptstyle \alpha {\vec {x}}+{\vec {y}}} přiřadilo vektor αu→+v→{\displaystyle \scriptstyle \alpha {\vec {u}}+{\vec {v}}}
přiřadilo vektor αu→+v→{\displaystyle \scriptstyle \alpha {\vec {u}}+{\vec {v}}} . Jeho inverze tedy učiní opak dostávajíc A−1(αu→+v→)=αx→+y→{\displaystyle \scriptstyle A^{-1}(\alpha {\vec {u}}+{\vec {v}})=\alpha {\vec {x}}+{\vec {y}}}
. Jeho inverze tedy učiní opak dostávajíc A−1(αu→+v→)=αx→+y→{\displaystyle \scriptstyle A^{-1}(\alpha {\vec {u}}+{\vec {v}})=\alpha {\vec {x}}+{\vec {y}}} . Když si rozepíšeme, jak vznikly vektory x→{\displaystyle \scriptstyle {\vec {x}}}
. Když si rozepíšeme, jak vznikly vektory x→{\displaystyle \scriptstyle {\vec {x}}} a y→{\displaystyle \scriptstyle {\vec {y}}}
a y→{\displaystyle \scriptstyle {\vec {y}}} dospíváme k výrazu A−1(αu→+v→)=αA−1(u→)+A−1(v→){\displaystyle \scriptstyle A^{-1}(\alpha {\vec {u}}+{\vec {v}})=\alpha A^{-1}({\vec {u}})+A^{-1}({\vec {v}})}
dospíváme k výrazu A−1(αu→+v→)=αA−1(u→)+A−1(v→){\displaystyle \scriptstyle A^{-1}(\alpha {\vec {u}}+{\vec {v}})=\alpha A^{-1}({\vec {u}})+A^{-1}({\vec {v}})} , což je ekvivalentní s linearitou zobrazení A−1{\displaystyle \scriptstyle A^{-1}}
, což je ekvivalentní s linearitou zobrazení A−1{\displaystyle \scriptstyle A^{-1}} .
.
Maticová reprezentace
Linearita nějakého zobrazení je natolik omezující vlastnost, že pro charakterizaci takovéhoto zobrazení stačí uvést jeho hodnoty jen v (relativně) malém počtu bodů. Tato vlastnost tím více vyplyne na konečněrozměrných vektorových prostorech. Pro konkrétnost tedy mějme lineární zobrazení A∈L(Xn,Ym){\displaystyle \scriptstyle A\in {\mathcal {L}}(X_{n},Y_{m})} , kde oba vektorové prostory jsou konečných dimenzí, dimXn=n,dimYm=m{\displaystyle \scriptstyle \dim X_{n}=n,\dim Y_{m}=m}
, kde oba vektorové prostory jsou konečných dimenzí, dimXn=n,dimYm=m{\displaystyle \scriptstyle \dim X_{n}=n,\dim Y_{m}=m} . V obou prostorech tedy existuje jejich báze, označme bazické vektory prostoru X jako x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}}
. V obou prostorech tedy existuje jejich báze, označme bazické vektory prostoru X jako x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}} a podobně nechť y→1,…,y→m{\displaystyle \scriptstyle {\vec {y}}_{1},\ldots ,{\vec {y}}_{m}}
a podobně nechť y→1,…,y→m{\displaystyle \scriptstyle {\vec {y}}_{1},\ldots ,{\vec {y}}_{m}} je báze prostoru Y. Libovolný vektor x→{\displaystyle \scriptstyle {\vec {x}}}
je báze prostoru Y. Libovolný vektor x→{\displaystyle \scriptstyle {\vec {x}}} z prostoru X lze tedy zapsat jako lineární kombinaci bazických vektorů
z prostoru X lze tedy zapsat jako lineární kombinaci bazických vektorů
x→=∑i=1nαix→i.{\displaystyle {\vec {x}}=\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}.}
Pak působením zobrazení A na takovýto vektor x→{\displaystyle \scriptstyle {\vec {x}}} dostáváme vektor A(x→)=y→{\displaystyle \scriptstyle A({\vec {x}})={\vec {y}}}
dostáváme vektor A(x→)=y→{\displaystyle \scriptstyle A({\vec {x}})={\vec {y}}} , pro nějž platí
, pro nějž platí
y→=A(x→)=A(∑i=1nαix→i)=∑i=1nαiA(x→i).{\displaystyle {\vec {y}}=A({\vec {x}})=A\left(\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}\right)=\sum _{i=1}^{n}\alpha _{i}A({\vec {x}}_{i}).}
Dále, vektory A(x→1),…,A(x→n){\displaystyle \scriptstyle A({\vec {x}}_{1}),\ldots ,A({\vec {x}}_{n})} leží v prostoru Y, takže je lze vyjádřit jako lineární kombinace bazických vektorů y→j{\displaystyle \scriptstyle {\vec {y}}_{j}}
leží v prostoru Y, takže je lze vyjádřit jako lineární kombinace bazických vektorů y→j{\displaystyle \scriptstyle {\vec {y}}_{j}} ve tvaru
ve tvaru
A(x→i)=∑j=1mβjiy→j.{\displaystyle A({\vec {x}}_{i})=\sum _{j=1}^{m}\beta _{ji}{\vec {y}}_{j}.}
Například pro vektor A(x→1){\displaystyle \scriptstyle A({\vec {x}}_{1})} tak máme A(x→1)=∑j=1mβj1y→j{\displaystyle \scriptstyle A({\vec {x}}_{1})=\sum _{j=1}^{m}\beta _{j1}{\vec {y}}_{j}}
tak máme A(x→1)=∑j=1mβj1y→j{\displaystyle \scriptstyle A({\vec {x}}_{1})=\sum _{j=1}^{m}\beta _{j1}{\vec {y}}_{j}} , pro vektor A(x→2){\displaystyle \scriptstyle A({\vec {x}}_{2})}
, pro vektor A(x→2){\displaystyle \scriptstyle A({\vec {x}}_{2})} máme A(x→2)=∑j=1mβj2y→j{\displaystyle \scriptstyle A({\vec {x}}_{2})=\sum _{j=1}^{m}\beta _{j2}{\vec {y}}_{j}}
máme A(x→2)=∑j=1mβj2y→j{\displaystyle \scriptstyle A({\vec {x}}_{2})=\sum _{j=1}^{m}\beta _{j2}{\vec {y}}_{j}} , pro vektor A(x→3){\displaystyle \scriptstyle A({\vec {x}}_{3})}
, pro vektor A(x→3){\displaystyle \scriptstyle A({\vec {x}}_{3})} máme A(x→3)=∑j=1mβj3y→j{\displaystyle \scriptstyle A({\vec {x}}_{3})=\sum _{j=1}^{m}\beta _{j3}{\vec {y}}_{j}}
máme A(x→3)=∑j=1mβj3y→j{\displaystyle \scriptstyle A({\vec {x}}_{3})=\sum _{j=1}^{m}\beta _{j3}{\vec {y}}_{j}} atd. Celkově tedy
atd. Celkově tedy
y→=∑i=1nαiA(x→i)=∑i=1nαi(∑j=1mβjiy→j)=∑i=1n∑j=1mαiβjiy→j.{\displaystyle {\vec {y}}=\sum _{i=1}^{n}\alpha _{i}A({\vec {x}}_{i})=\sum _{i=1}^{n}\alpha _{i}\left(\sum _{j=1}^{m}\beta _{ji}{\vec {y}}_{j}\right)=\sum _{i=1}^{n}\sum _{j=1}^{m}\alpha _{i}\beta _{ji}{\vec {y}}_{j}.}
Rozeberme nyní právě obdržený výraz. Koeficienty αi{\displaystyle \scriptstyle \alpha _{i}} v tomto výrazu pocházejí z lineární kombinace pro vstupní vektor x→{\displaystyle \scriptstyle {\vec {x}}}
v tomto výrazu pocházejí z lineární kombinace pro vstupní vektor x→{\displaystyle \scriptstyle {\vec {x}}} a vektory y→j{\displaystyle \scriptstyle {\vec {y}}_{j}}
a vektory y→j{\displaystyle \scriptstyle {\vec {y}}_{j}} jsou předem zadaná báze prostoru Y. Jediné, co tedy charakterizuje zobrazení A samotné jsou tak prvky βji{\displaystyle \scriptstyle \beta _{ji}}
jsou předem zadaná báze prostoru Y. Jediné, co tedy charakterizuje zobrazení A samotné jsou tak prvky βji{\displaystyle \scriptstyle \beta _{ji}} . Tyto si můžeme uspořádat do matice tvaru
. Tyto si můžeme uspořádat do matice tvaru
(β11β12β13…β1nβ21β22β23…β2nβ31β32β33…β3n⋮⋮⋮⋱⋮βm1βm2βm3…βmn).{\displaystyle {\begin{pmatrix}\beta _{11}&\beta _{12}&\beta _{13}&\dots &\beta _{1n}\\\beta _{21}&\beta _{22}&\beta _{23}&\dots &\beta _{2n}\\\beta _{31}&\beta _{32}&\beta _{33}&\dots &\beta _{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\\beta _{m1}&\beta _{m2}&\beta _{m3}&\dots &\beta _{mn}\end{pmatrix}}.}
Této matici se říká matice zobrazení A v bázích X{\displaystyle \scriptstyle {\mathcal {X}}} a Y{\displaystyle \scriptstyle {\mathcal {Y}}}
a Y{\displaystyle \scriptstyle {\mathcal {Y}}} , kde jsme označili bázi prostoru X jako X={x→1,…,x→n}{\displaystyle \scriptstyle {\mathcal {X}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}}
, kde jsme označili bázi prostoru X jako X={x→1,…,x→n}{\displaystyle \scriptstyle {\mathcal {X}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}} a bázi prostoru Y jako Y={y→1,…,y→m}{\displaystyle \scriptstyle {\mathcal {Y}}=\{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}}
a bázi prostoru Y jako Y={y→1,…,y→m}{\displaystyle \scriptstyle {\mathcal {Y}}=\{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}} . Tato matice plně popisuje strukturu lineárního zobrazení A. Značí se symbolem
. Tato matice plně popisuje strukturu lineárního zobrazení A. Značí se symbolem
XAY{\displaystyle {}^{\mathcal {X}}A^{\mathcal {Y}}} .
.
Násobení matic
Máme-li matici A typu m×s a matici B typu s×n, pak jejich součinem je matice C typu m×n, který značíme
C=A⋅B{\displaystyle \mathbf {C} =\mathbf {A} \cdot \mathbf {B} } ,
,
přičemž prvky matice C jsou určeny jako
cij=∑k=1saikbkj{\displaystyle c_{ij}=\sum _{k=1}^{s}a_{ik}b_{kj}}
nebo
cji=∑k=1sakibjk{\displaystyle c_{j}^{i}=\sum _{k=1}^{s}a_{k}^{i}b_{j}^{k}} .
.
Gaussova eliminace
Gaussova eliminační metoda (Gaussova eliminace) je metodou řešení soustavy lineárních algebraických rovnic. Jedná se o metodu konečnou, tj. metodu vedoucí k (alespoň teoreticky) přesnému řešení v konečně mnoha krocích, postavenou na tzv. LU rozkladu matice soustavy. Lze dokázat, že Gaussova eliminace převede každou matici do odstupňovaného tvaru (tvar, kde počet nul na začátku i{\displaystyle i} -tého řádku je alespoň takový jako počet nul na začátku (i−1){\displaystyle (i-1)}
-tého řádku je alespoň takový jako počet nul na začátku (i−1){\displaystyle (i-1)} -tého řádku). [1]
-tého řádku). [1]
Sloupcový & řádkový prostor
In linear algebra, the column space (also called the range or image) of a matrix A is the span (set of all possible linear combinations) of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.
Let F{\displaystyle \mathbb {F} } be a field. The column space of an m × n matrix with components from F{\displaystyle \mathbb {F} }
be a field. The column space of an m × n matrix with components from F{\displaystyle \mathbb {F} } is a linear subspace of the m-space Fm{\displaystyle \mathbb {F} ^{m}}
is a linear subspace of the m-space Fm{\displaystyle \mathbb {F} ^{m}} . The dimension of the column space is called the rank of the matrix and is at most min(m, n).[1] A definition for matrices over a ring K{\displaystyle \mathbb {K} }
. The dimension of the column space is called the rank of the matrix and is at most min(m, n).[1] A definition for matrices over a ring K{\displaystyle \mathbb {K} } is also possible.
is also possible.
The row space is defined similarly.
The row space and the column space of a matrix A are sometimes denoted as C(AT) and C(A) respectively.[2]
This article considers matrices of real numbers. The row and column spaces are subspaces of the real spaces Rn{\displaystyle \mathbb {R} ^{n}} and Rm{\displaystyle \mathbb {R} ^{m}}
and Rm{\displaystyle \mathbb {R} ^{m}} respectively.
respectively.
Lineární závislost
Vektory x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}} jsou lineárně závislé, právě když platí
jsou lineárně závislé, právě když platí
(∃(α1,…,αk)∈Tk)(∑i=1kαix→i=0→∧∑i=1k|αi|>0).{\displaystyle {\Big (}\exists (\alpha _{1},\ldots ,\alpha _{k})\in T^{k}{\Big )}\left(\sum _{i=1}^{k}\alpha _{i}{\vec {x}}_{i}={\vec {0}}\quad \wedge \quad \sum _{i=1}^{k}|\alpha _{i}|>0\right).}
Isomorfismus
Předpokládejme, že na množině X{\displaystyle X\,\!} jsou definovány relace R1,R2,…,Rn{\displaystyle R_{1},R_{2},\ldots ,R_{n}\,\!}
jsou definovány relace R1,R2,…,Rn{\displaystyle R_{1},R_{2},\ldots ,R_{n}\,\!} a na množině Y{\displaystyle Y\,\!}
a na množině Y{\displaystyle Y\,\!} jsou definovány relace S1,S2,…,Sn{\displaystyle S_{1},S_{2},\ldots ,S_{n}\,\!}
jsou definovány relace S1,S2,…,Sn{\displaystyle S_{1},S_{2},\ldots ,S_{n}\,\!} . Řekneme, že zobrazení F{\displaystyle F\,\!}
. Řekneme, že zobrazení F{\displaystyle F\,\!} je izomorfismus mezi X{\displaystyle X\,\!}
je izomorfismus mezi X{\displaystyle X\,\!} a Y{\displaystyle Y\,\!}
a Y{\displaystyle Y\,\!} vzhledem k relacím R1,R2,…,Rn{\displaystyle R_{1},R_{2},\ldots ,R_{n}\,\!}
vzhledem k relacím R1,R2,…,Rn{\displaystyle R_{1},R_{2},\ldots ,R_{n}\,\!} a S1,S2,…,Sn{\displaystyle S_{1},S_{2},\ldots ,S_{n}\,\!}
a S1,S2,…,Sn{\displaystyle S_{1},S_{2},\ldots ,S_{n}\,\!} , pokud platí:
, pokud platí:
- F{\displaystyle F\,\!}
 je vzájemně jednoznačné zobrazení mezi X{\displaystyle X\,\!}
je vzájemně jednoznačné zobrazení mezi X{\displaystyle X\,\!} a Y{\displaystyle Y\,\!}
a Y{\displaystyle Y\,\!}
- pokud jsou Ri,Si{\displaystyle R_{i},S_{i}\,\!}
 j-ární relace, potom ∀x1,x2,…,xj∈X:[x1,x2,…,xj]∈Ri⇔[F(x1),F(x2),…,F(xj)]∈Si{\displaystyle \forall x_{1},x_{2},\ldots ,x_{j}\in X:[x_{1},x_{2},\ldots ,x_{j}]\in R_{i}\Leftrightarrow [F(x_{1}),F(x_{2}),\ldots ,F(x_{j})]\in S_{i}\,\!}
j-ární relace, potom ∀x1,x2,…,xj∈X:[x1,x2,…,xj]∈Ri⇔[F(x1),F(x2),…,F(xj)]∈Si{\displaystyle \forall x_{1},x_{2},\ldots ,x_{j}\in X:[x_{1},x_{2},\ldots ,x_{j}]\in R_{i}\Leftrightarrow [F(x_{1}),F(x_{2}),\ldots ,F(x_{j})]\in S_{i}\,\!} .
.
Řekneme, že struktury X,R1,R2,…,Rn{\displaystyle X,R_{1},R_{2},\ldots ,R_{n}\,\!} a Y,S1,S2,…,Sn{\displaystyle Y,S_{1},S_{2},\ldots ,S_{n}\,\!}
a Y,S1,S2,…,Sn{\displaystyle Y,S_{1},S_{2},\ldots ,S_{n}\,\!} jsou izomorfní, pokud mezi nimi existuje nějaký izomorfismus ve smyslu výše uvedené definice.
jsou izomorfní, pokud mezi nimi existuje nějaký izomorfismus ve smyslu výše uvedené definice.
RREF tvar matice
A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions:[3]
- It is in row echelon form.
- The leading entry in each nonzero row is a 1 (called a leading 1).
- Each column containing a leading 1 has zeros in all its other entries.
REF tvar matice
Matice A∈Rm×n je v řádkově odstupňovaném tvaru, pokud existuje r takové, že platí
- řádky 1, . . . ,r jsou nenulové(tj. každý obsahuje alespoň jednu nenulovou hodnotu),
- řádky r+1, . . . ,m jsou nulové,a navíc označíme-li jako pi= min{j;aij!=0} pozici prvníhon enulového prvku v i-tém řádku, tak platí
p1<p2<· · ·<p
Maticové prostory
Matice přechodu
Matice jsou užitečný nástroj na spočtení souřadnic vektoru v nějaké bázi, pokud známe jeho souřadnice v jiné bázi. Pokud {e1,…,en}{\displaystyle \scriptstyle \{e_{1},\ldots ,e_{n}\}} a {e1′,…,en′}{\displaystyle \scriptstyle \{e_{1}',\ldots ,e_{n}'\}}
a {e1′,…,en′}{\displaystyle \scriptstyle \{e_{1}',\ldots ,e_{n}'\}} jsou dvě báze, pro které platí ej′=∑ieiaji,{\displaystyle \scriptstyle e_{j}'=\sum _{i}e_{i}a_{\,\,j}^{i},}
jsou dvě báze, pro které platí ej′=∑ieiaji,{\displaystyle \scriptstyle e_{j}'=\sum _{i}e_{i}a_{\,\,j}^{i},} , neboli
, neboli
(e1′,…,en′)=(e1,…,en)A,{\displaystyle (e_{1}',\ldots ,e_{n}')=(e_{1},\ldots ,e_{n})A,}
pak matice A=(aji){\displaystyle \scriptstyle \mathbf {A} =(a_{\,\,j}^{i})} se nazývá matice přechodu od báze {ei}i{\displaystyle \scriptstyle \{e_{i}\}_{i}}
se nazývá matice přechodu od báze {ei}i{\displaystyle \scriptstyle \{e_{i}\}_{i}} k bázi {ei′}i{\displaystyle \scriptstyle \{e_{i}'\}_{i}}
k bázi {ei′}i{\displaystyle \scriptstyle \{e_{i}'\}_{i}} . Pro souřadnice pak platí
. Pro souřadnice pak platí
A−1(x1…xn){ei}i=(x′1…x′n){ei′}i,{\displaystyle \mathbf {A} ^{-1}\left({\begin{array}{c}x^{1}\\\ldots \\x^{n}\end{array}}\right)_{\{e_{i}\}_{i}}=\left({\begin{array}{c}x'^{1}\\\ldots \\x'^{n}\end{array}}\right)_{\{e_{i}'\}_{i}},}
kde xi{\displaystyle \scriptstyle x^{i}} jsou souřadnice libovolného vektoru v bázi {ei}i{\displaystyle \scriptstyle \{e_{i}\}_{i}}
jsou souřadnice libovolného vektoru v bázi {ei}i{\displaystyle \scriptstyle \{e_{i}\}_{i}} a x′i{\displaystyle \scriptstyle x'^{i}}
a x′i{\displaystyle \scriptstyle x'^{i}} jsou jeho souřadnice v bázi {ei′}i{\displaystyle \scriptstyle \{e_{i}'\}_{i}}
jsou jeho souřadnice v bázi {ei′}i{\displaystyle \scriptstyle \{e_{i}'\}_{i}} a A−1{\displaystyle \scriptstyle \mathbf {A} ^{-1}}
a A−1{\displaystyle \scriptstyle \mathbf {A} ^{-1}} je inverzní matice k matici A{\displaystyle \scriptstyle \mathbf {A} }
je inverzní matice k matici A{\displaystyle \scriptstyle \mathbf {A} } .
.
Úpravy
Obraz
Buď f:U→V lineární zobrazení. Pak definujeme
obraz f(U):={f(x);x∈U}
Prostor
Prostor je v matematice obvykle označení pro geometrický, topologický případně množinový objekt. V užším smyslu se prostorem rozumí třírozměrný fyzikální prostor, v kterém jsme zvyklí si vytvářet své geometrické představy. Obecněji může prostor znamenat v závislosti na kontextu topologický prostor,[1] varietu, metrický prostor, [2] množinu s nějakou přidanou algebraickou strukturou,[3] vektorový prostor,[4] anebo jenom samotnou množinu.[5]
Lineární kombinace
Uvažujme vektorový prostor V{\displaystyle \scriptstyle V} nad tělesem T{\displaystyle \scriptstyle T}
nad tělesem T{\displaystyle \scriptstyle T} . Dále nechť x→∈V{\displaystyle \scriptstyle {\vec {x}}\in V}
. Dále nechť x→∈V{\displaystyle \scriptstyle {\vec {x}}\in V} je nějaký vektor a x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}}
je nějaký vektor a x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}} je soubor k{\displaystyle \scriptstyle k}
je soubor k{\displaystyle \scriptstyle k} vektorů z prostoru V{\displaystyle \scriptstyle V}
vektorů z prostoru V{\displaystyle \scriptstyle V} . Pak říkáme, že vektor x→{\displaystyle \scriptstyle {\vec {x}}}
. Pak říkáme, že vektor x→{\displaystyle \scriptstyle {\vec {x}}} je lineární kombinací (angl. linear combination) vektorů x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}}
je lineární kombinací (angl. linear combination) vektorů x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}} , právě když existuje k{\displaystyle \scriptstyle k}
, právě když existuje k{\displaystyle \scriptstyle k} -tice čísel z tělesa α1,…,αk∈T{\displaystyle \scriptstyle \alpha _{1},\ldots ,\alpha _{k}\in T}
-tice čísel z tělesa α1,…,αk∈T{\displaystyle \scriptstyle \alpha _{1},\ldots ,\alpha _{k}\in T} taková, že lze vektor x→{\displaystyle \scriptstyle {\vec {x}}}
taková, že lze vektor x→{\displaystyle \scriptstyle {\vec {x}}} vyjádřit ve tvaru sumy
vyjádřit ve tvaru sumy
x→=α1x→1+…+αkx→k=∑i=1kαix→i.{\displaystyle {\vec {x}}=\alpha _{1}{\vec {x}}_{1}+\ldots +\alpha _{k}{\vec {x}}_{k}=\sum _{i=1}^{k}\alpha _{i}{\vec {x}}_{i}.}
Gauss-Jordanova eliminace
Vektorový podprostor
Mějme vektorový prostor V{\displaystyle \scriptstyle V} nad tělesem T{\displaystyle \scriptstyle T}
nad tělesem T{\displaystyle \scriptstyle T} . Dále buď P{\displaystyle \scriptstyle P}
. Dále buď P{\displaystyle \scriptstyle P} neprázdná podmnožina prostoru V{\displaystyle \scriptstyle V}
neprázdná podmnožina prostoru V{\displaystyle \scriptstyle V} , která splňuje
, která splňuje
- (∀x→∈P)(∀y→∈P)(x→+y→∈P),{\displaystyle (\forall {\vec {x}}\in P)(\forall {\vec {y}}\in P)({\vec {x}}+{\vec {y}}\in P),}

- (∀α∈T)(∀x→∈P)(αx→∈P).{\displaystyle (\forall \alpha \in T)(\forall {\vec {x}}\in P)(\alpha {\vec {x}}\in P).}

Pak množinu P{\displaystyle \scriptstyle P} nazýváme podprostorem vektorového prostoru V{\displaystyle \scriptstyle V}
nazýváme podprostorem vektorového prostoru V{\displaystyle \scriptstyle V} a značíme P⊂⊂V{\displaystyle \scriptstyle P\subset \subset V}
a značíme P⊂⊂V{\displaystyle \scriptstyle P\subset \subset V} .
.
Vektor
V matematice je vektor definován jako prvek vektorového prostoru. V něm lze zavést bázi a dále souřadnice daného vektoru vzhledem k této bázi. Pokud je vektorový prostor konečnědimenzionální, souřadnice vektoru tvoří uspořádané n-tice čísel, označovaných jako složky (též komponenty) vektoru. Speciálně, pokud se za vektorový prostor volí kartézský součin množin reálných či komplexních čísel, tj. pokud je za vektorový prostor bráno Rn{\displaystyle \scriptstyle \mathbb {R} ^{n}} či Cn{\displaystyle \scriptstyle \mathbb {C} ^{n}}
či Cn{\displaystyle \scriptstyle \mathbb {C} ^{n}} pro nějaké přirozené číslo n, tak se jeho prvky nazývají aritmetické vektory. Počet složek vektoru je roven dimenzi vektorového prostoru.
pro nějaké přirozené číslo n, tak se jeho prvky nazývají aritmetické vektory. Počet složek vektoru je roven dimenzi vektorového prostoru.
Dimenze
Nechť V{\displaystyle \scriptstyle V} je vektorový prostor a uvažujme podmnožinu množiny přirozených čísel, kterou označíme N0{\displaystyle \scriptstyle N_{0}}
je vektorový prostor a uvažujme podmnožinu množiny přirozených čísel, kterou označíme N0{\displaystyle \scriptstyle N_{0}} a definujeme vztahem
a definujeme vztahem
N0={n∈N∪{0}| každý (n+1)−členný soubor vektorů z V je lineárně závislý}.{\displaystyle N_{0}=\{n\in \mathbb {N} \cup \{0\}|{\text{ každý }}(n+1)-{\text{členný soubor vektorů z }}V{\text{ je lineárně závislý}}\}.}
Jestliže je množina N0{\displaystyle \scriptstyle N_{0}} neprázdná, tak říkáme, že vektorový prostor V{\displaystyle \scriptstyle V}
neprázdná, tak říkáme, že vektorový prostor V{\displaystyle \scriptstyle V} má konečnou dimenzi, která je rovna číslu minN0{\displaystyle \scriptstyle \min N_{0}}
má konečnou dimenzi, která je rovna číslu minN0{\displaystyle \scriptstyle \min N_{0}} . Značíme,
. Značíme,
dimV=minN0.{\displaystyle \dim V=\min N_{0}.}
Pokud je množina N0{\displaystyle \scriptstyle N_{0}} prázdná, tj. N0=∅{\displaystyle \scriptstyle N_{0}=\emptyset }
prázdná, tj. N0=∅{\displaystyle \scriptstyle N_{0}=\emptyset } , tak říkáme, že vektorový prostor V{\displaystyle \scriptstyle V}
, tak říkáme, že vektorový prostor V{\displaystyle \scriptstyle V} má nekonečnou dimenzi a píšeme
má nekonečnou dimenzi a píšeme
dimV=∞.{\displaystyle \dim V=\infty .}
Soustavy lineárních rovnic
Obecně může být soustava m lineárních rovnic s n proměnnými zapsána jako
a11x1 + a12x2 + … + a1nxn = b1a21x1 + a22x2 + … + a2nxn = b2 : :am1x1 + am2x2 + … + amnxn = bm,
kde proměnné x1, … ,xn jsou neznámé a aij jsou koeficienty soustavy rovnic. Čísla bi{\displaystyle b_{i}} , kde i=1,2,...,m{\displaystyle i=1,2,...,m}
, kde i=1,2,...,m{\displaystyle i=1,2,...,m} , jsou absolutní členy soustavy (nebo také tzv. pravá strana soustavy). V obecném případě mohou být koeficienty i absolutní členy komplexními čísly.
, jsou absolutní členy soustavy (nebo také tzv. pravá strana soustavy). V obecném případě mohou být koeficienty i absolutní členy komplexními čísly.
Koeficienty lze zapsat ve tvaru matice:
A=(a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn){\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}}
Tuto matici označujeme jako matici soustavy.
Vektorový prostor
Nechť jsou dány
- neprázdná množina V{\displaystyle \scriptstyle V}
 , jejíž prvky nazýváme vektory,
, jejíž prvky nazýváme vektory, - těleso T{\displaystyle \scriptstyle T}
 (s operacemi sčítání + a násobení ⋅{\displaystyle \scriptstyle \cdot }
(s operacemi sčítání + a násobení ⋅{\displaystyle \scriptstyle \cdot } ),
), - zobrazení ⊕: V×V→V{\displaystyle \scriptstyle \oplus :\ V\times V\to V}
 , jež nazýváme sčítání vektorů,
, jež nazýváme sčítání vektorů, - zobrazení ⊙: T×V→V{\displaystyle \scriptstyle \odot :\ T\times V\to V}
 , jež nazýváme násobení vektorů (prvkem z tělesa).
, jež nazýváme násobení vektorů (prvkem z tělesa).
Řekneme, že V{\displaystyle \scriptstyle V} je vektorový prostor nad tělesem T{\displaystyle \scriptstyle T}
je vektorový prostor nad tělesem T{\displaystyle \scriptstyle T} s vektorovými operacemi ⊕,⊙{\displaystyle \scriptstyle \oplus ,\odot }
s vektorovými operacemi ⊕,⊙{\displaystyle \scriptstyle \oplus ,\odot } , právě když je množina V{\displaystyle \scriptstyle V}
, právě když je množina V{\displaystyle \scriptstyle V} uzavřená na operace ⊕{\displaystyle \scriptstyle \oplus }
uzavřená na operace ⊕{\displaystyle \scriptstyle \oplus } a ⊙{\displaystyle \scriptstyle \odot }
a ⊙{\displaystyle \scriptstyle \odot } a současně platí tzv. axiomy vektorového prostoru. Těchto axiomů je osm a jejich znění je následující:
a současně platí tzv. axiomy vektorového prostoru. Těchto axiomů je osm a jejich znění je následující:
Axiomy vektorového prostoru| Č. | Slovně | Symbolicky |
|---|
| 1 | komutativita pro sčítání vektorů | (∀x→∈V)(∀y→∈V)(x→⊕y→=y→⊕x→){\displaystyle (\forall {\vec {x}}\in V)(\forall {\vec {y}}\in V)({\vec {x}}\oplus {\vec {y}}={\vec {y}}\oplus {\vec {x}})} |
| 2 | asociativita pro sčítání vektorů | (∀x→∈V)(∀y→∈V)(∀z→∈V)((x→⊕y→)⊕z→=x→⊕(y→⊕z→)){\displaystyle (\forall {\vec {x}}\in V)(\forall {\vec {y}}\in V)(\forall {\vec {z}}\in V)(({\vec {x}}\oplus {\vec {y}})\oplus {\vec {z}}={\vec {x}}\oplus ({\vec {y}}\oplus {\vec {z}}))} |
| 3 | existence nulového vektoru | (∃0→∈V)(∀x→∈V)(x→⊕0→=x→){\displaystyle (\exists {\vec {0}}\in V)(\forall {\vec {x}}\in V)({\vec {x}}\oplus {\vec {0}}={\vec {x}})} |
| 4 | existence opačného vektoru | (∀x→∈V)(∃y→∈V)(x→⊕y→=0→){\displaystyle (\forall {\vec {x}}\in V)(\exists {\vec {y}}\in V)({\vec {x}}\oplus {\vec {y}}={\vec {0}})} |
| 5 | asociativita pro násobení vektoru | (∀α∈T)(∀β∈T)(∀x→∈V)(α⊙(β⊙x→)=(α⋅β)⊙x→){\displaystyle (\forall \alpha \in T)(\forall \beta \in T)(\forall {\vec {x}}\in V)(\alpha \odot (\beta \odot {\vec {x}})=(\alpha \cdot \beta )\odot {\vec {x}})} |
| 6 | invariance vektoru při vynásobení jednotkovým prvkem tělesa | (∀x→∈V)(1⊙x→=x→){\displaystyle (\forall {\vec {x}}\in V)(1\odot {\vec {x}}={\vec {x}})} |
| 7 | distributivita násobení vektoru vzhledem ke sčítání prvků tělesa | (∀α∈T)(∀β∈T)(∀x→∈V)((α+β)⊙x→=(α⊙x→)⊕(β⊙x→)){\displaystyle (\forall \alpha \in T)(\forall \beta \in T)(\forall {\vec {x}}\in V)((\alpha +\beta )\odot {\vec {x}}=(\alpha \odot {\vec {x}})\oplus (\beta \odot {\vec {x}}))} |
| 8 | distributivita násobení vektoru vzhledem ke sčítání vektorů | (∀α∈T)(∀x→∈V)(∀y→∈V)(α⊙(x→⊕y→)=(α⊙x→)⊕(α⊙y→)){\displaystyle (\forall \alpha \in T)(\forall {\vec {x}}\in V)(\forall {\vec {y}}\in V)(\alpha \odot ({\vec {x}}\oplus {\vec {y}})=(\alpha \odot {\vec {x}})\oplus (\alpha \odot {\vec {y}}))} |
Lineární nezávislost
Buď V{\displaystyle \scriptstyle V} vektorový prostor nad tělesem T{\displaystyle \scriptstyle T}
vektorový prostor nad tělesem T{\displaystyle \scriptstyle T} a mějme dále soubor vektorů x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}}
a mějme dále soubor vektorů x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}} pro jisté přirozené číslo k≥1{\displaystyle \scriptstyle k\geq 1}
pro jisté přirozené číslo k≥1{\displaystyle \scriptstyle k\geq 1} . Uvažujme pak všechny možné lineární kombinace tohoto souboru vektorů, které jsou rovny nulovému vektoru. Pak říkáme, že soubor x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}}
. Uvažujme pak všechny možné lineární kombinace tohoto souboru vektorů, které jsou rovny nulovému vektoru. Pak říkáme, že soubor x→1,…,x→k{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{k}} je lineárně nezávislý, právě když ze všech lineárních kombinací těchto vektorů je rovna nulovému vektoru jen triviální lineární kombinace. V opačném případě nazýváme soubor výše lineárně závislý.
je lineárně nezávislý, právě když ze všech lineárních kombinací těchto vektorů je rovna nulovému vektoru jen triviální lineární kombinace. V opačném případě nazýváme soubor výše lineárně závislý.
Algebraická tělesa
Konečná tělesa
Trojici (F,+,⋅){\displaystyle ({\mathcal {F}},+,\cdot )} , kde F{\displaystyle {\mathcal {F}}}
, kde F{\displaystyle {\mathcal {F}}} je množina a + (sčítání) a ⋅{\displaystyle \cdot }
je množina a + (sčítání) a ⋅{\displaystyle \cdot } (násobení) jsou binární operace, nazveme tělesem, je-li (F,+,⋅){\displaystyle ({\mathcal {F}},+,\cdot )}
(násobení) jsou binární operace, nazveme tělesem, je-li (F,+,⋅){\displaystyle ({\mathcal {F}},+,\cdot )} okruh a platí-li navíc
okruh a platí-li navíc
- pro každé x∈F∖{0}{\displaystyle x\in {\mathcal {F}}\setminus \{0\}}
 existuje y∈F{\displaystyle y\in {\mathcal {F}}}
existuje y∈F{\displaystyle y\in {\mathcal {F}}} takové, že x⋅y=y⋅x=1{\displaystyle x\cdot y=y\cdot x=1}
takové, že x⋅y=y⋅x=1{\displaystyle x\cdot y=y\cdot x=1} , což značíme y=x−1{\displaystyle y=x^{-1}}
, což značíme y=x−1{\displaystyle y=x^{-1}} .
.
Grupy
Grupou nazýváme množinu G{\displaystyle G} spolu s binární operací na ní, která se nazývá grupová operace. Tato operace libovolným dvěma prvkům grupy a,b{\displaystyle a,b}
spolu s binární operací na ní, která se nazývá grupová operace. Tato operace libovolným dvěma prvkům grupy a,b{\displaystyle a,b} přiřazuje prvek téže grupy c{\displaystyle c}
přiřazuje prvek téže grupy c{\displaystyle c} . Značení grupové operace se v literatuře liší. Obvykle se značí jako násobení c=a⋅b{\displaystyle c=a\cdot b}
. Značení grupové operace se v literatuře liší. Obvykle se značí jako násobení c=a⋅b{\displaystyle c=a\cdot b} , resp. jenom c=ab{\displaystyle c=ab}
, resp. jenom c=ab{\displaystyle c=ab} , v Abelových grupách často jako sčítání c=a+b{\displaystyle c=a+b}
, v Abelových grupách často jako sčítání c=a+b{\displaystyle c=a+b} , a někdy také pomocí dalších symbolů (a∘b{\displaystyle a\circ b}
, a někdy také pomocí dalších symbolů (a∘b{\displaystyle a\circ b} , resp. a∗b{\displaystyle a*b}
, resp. a∗b{\displaystyle a*b} ). Podle kontextu říkáme, že c{\displaystyle c}
). Podle kontextu říkáme, že c{\displaystyle c} je složení, resp. součin, resp. součet prvků a{\displaystyle a}
je složení, resp. součin, resp. součet prvků a{\displaystyle a} a b{\displaystyle b}
a b{\displaystyle b} . Dále se v definici grupy požaduje, aby grupová operace splňovala určité vlastnosti, které se nazývají axiomy grupy.[1]
. Dále se v definici grupy požaduje, aby grupová operace splňovala určité vlastnosti, které se nazývají axiomy grupy.[1]
Uzavřenost
Pro všechny prvky a,b{\displaystyle a,b} v G{\displaystyle G}
v G{\displaystyle G} je i složení a⋅b{\displaystyle a\cdot b}
je i složení a⋅b{\displaystyle a\cdot b} prvkem G{\displaystyle G}
prvkem G{\displaystyle G} .[pozn 1]
.[pozn 1]
Asociativita
Pro všechny prvky a,b,c{\displaystyle a,b,c} grupy G{\displaystyle G}
grupy G{\displaystyle G} platí a⋅(b⋅c)=(a⋅b)⋅c{\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c}
platí a⋅(b⋅c)=(a⋅b)⋅c{\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} , tj. výsledek složení tří prvků nezávisí na umístění závorek.[pozn 2] Díky tomu má smysl psát složení tří a více prvků a⋅b⋅c{\displaystyle a\cdot b\cdot c}
, tj. výsledek složení tří prvků nezávisí na umístění závorek.[pozn 2] Díky tomu má smysl psát složení tří a více prvků a⋅b⋅c{\displaystyle a\cdot b\cdot c} i bez závorek.
i bez závorek.
Existence neutrálního prvku
Existuje prvek e∈G{\displaystyle e\in G} takový, že pro všechna a∈G{\displaystyle a\in G}
takový, že pro všechna a∈G{\displaystyle a\in G} platí a⋅e=e⋅a=a{\displaystyle a\cdot e=e\cdot a=a}
platí a⋅e=e⋅a=a{\displaystyle a\cdot e=e\cdot a=a} . Tento prvek se nazývá neutrální prvek anebo jednotkový prvek a značí se také 1{\displaystyle 1}
. Tento prvek se nazývá neutrální prvek anebo jednotkový prvek a značí se také 1{\displaystyle 1} , resp. 1G{\displaystyle 1_{G}}
, resp. 1G{\displaystyle 1_{G}} .[pozn 3]
.[pozn 3]
Existence inverzního prvku
Pro každý prvek grupy a{\displaystyle a} existuje prvek b{\displaystyle b}
existuje prvek b{\displaystyle b} takový, že a⋅b=b⋅a=e{\displaystyle a\cdot b=b\cdot a=e}
takový, že a⋅b=b⋅a=e{\displaystyle a\cdot b=b\cdot a=e} , tj. jejich složení v libovolném pořadí je rovno neutrálnímu prvku e{\displaystyle e}
, tj. jejich složení v libovolném pořadí je rovno neutrálnímu prvku e{\displaystyle e} . Prvek b{\displaystyle b}
. Prvek b{\displaystyle b} se také nazývá inverzní prvek k a{\displaystyle a}
se také nazývá inverzní prvek k a{\displaystyle a} a značí se a−1{\displaystyle a^{-1}}
a značí se a−1{\displaystyle a^{-1}} . Lze ukázat, že neutrální prvek je v grupě jenom jeden a že inverzní prvek k a{\displaystyle a}
. Lze ukázat, že neutrální prvek je v grupě jenom jeden a že inverzní prvek k a{\displaystyle a} je dán jednoznačně.
je dán jednoznačně.
V grupách obecně záleží na pořadí, ve kterém prvky skládáme, tj. obecně nemusí platit a⋅b=b⋅a{\displaystyle a\cdot b=b\cdot a} . Grupa, ve které tato rovnost platí pro všechna a,b{\displaystyle a,b}
. Grupa, ve které tato rovnost platí pro všechna a,b{\displaystyle a,b} , se nazývá komutativní grupa nebo také Abelova grupa.
, se nazývá komutativní grupa nebo také Abelova grupa.
Steinitzova věta o výměně
Nechť X≡{x→1,…,x→n}{\displaystyle \scriptstyle X\equiv \{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}} a Y≡{y→1,…,y→m}{\displaystyle \scriptstyle Y\equiv \{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}}
a Y≡{y→1,…,y→m}{\displaystyle \scriptstyle Y\equiv \{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}} jsou dvě množiny vektorů z vektorového prostoru V{\displaystyle \scriptstyle V}
jsou dvě množiny vektorů z vektorového prostoru V{\displaystyle \scriptstyle V} . Nechť jsou dále vektory z množiny X{\displaystyle \scriptstyle X}
. Nechť jsou dále vektory z množiny X{\displaystyle \scriptstyle X} lineárně nezávislé a každý z nich lze vyjádřit jako lineární kombinaci vektorů z množiny Y{\displaystyle \scriptstyle Y}
lineárně nezávislé a každý z nich lze vyjádřit jako lineární kombinaci vektorů z množiny Y{\displaystyle \scriptstyle Y} . Pak platí, že n≤m{\displaystyle \scriptstyle n\leq m}
. Pak platí, že n≤m{\displaystyle \scriptstyle n\leq m} . Pokud n=m{\displaystyle \scriptstyle n=m}
. Pokud n=m{\displaystyle \scriptstyle n=m} , tak je lineární obal množiny X{\displaystyle \scriptstyle X}
, tak je lineární obal množiny X{\displaystyle \scriptstyle X} nutně roven lineárnímu obalu množiny Y{\displaystyle \scriptstyle Y}
nutně roven lineárnímu obalu množiny Y{\displaystyle \scriptstyle Y} . Neboli {X}lin={x→1,…,x→n}lin={y→1,…,y→m}lin={Y}lin{\displaystyle \scriptstyle \{X\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}=\{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}}=\{Y\}_{\text{lin}}}
. Neboli {X}lin={x→1,…,x→n}lin={y→1,…,y→m}lin={Y}lin{\displaystyle \scriptstyle \{X\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}=\{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}}=\{Y\}_{\text{lin}}} . (Výraz {X}lin{\displaystyle \scriptstyle \{X\}_{\text{lin}}}
. (Výraz {X}lin{\displaystyle \scriptstyle \{X\}_{\text{lin}}} značí lineární obal množiny X{\displaystyle \scriptstyle X}
značí lineární obal množiny X{\displaystyle \scriptstyle X} atd.). Dále, pokud platí ostrá nerovnost n<m{\displaystyle \scriptstyle n<m}
atd.). Dále, pokud platí ostrá nerovnost n<m{\displaystyle \scriptstyle n<m} , tak existují navzájem různé indexy i1,…,im−n∈{1,…,m}{\displaystyle \scriptstyle i_{1},\ldots ,i_{m-n}\in \{1,\ldots ,m\}}
, tak existují navzájem různé indexy i1,…,im−n∈{1,…,m}{\displaystyle \scriptstyle i_{1},\ldots ,i_{m-n}\in \{1,\ldots ,m\}} takové, že
takové, že
{y→1,…,y→m}lin={x→1,…,x→n,y→i1,…,y→im−n}lin.{\displaystyle \{{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n},{\vec {y}}_{i_{1}},\ldots ,{\vec {y}}_{i_{m-n}}\}_{\text{lin}}.}
Generátory
Mějme vektorový prostor V{\displaystyle \scriptstyle V} a dále jeho jistou neprázdnou podmnožinu X⊂V{\displaystyle \scriptstyle X\subset V}
a dále jeho jistou neprázdnou podmnožinu X⊂V{\displaystyle \scriptstyle X\subset V} . Pak říkáme, že množina X{\displaystyle \scriptstyle X}
. Pak říkáme, že množina X{\displaystyle \scriptstyle X} generuje vektorový prostor V{\displaystyle \scriptstyle V}
generuje vektorový prostor V{\displaystyle \scriptstyle V} , právě když lze každý vektor z prostoru V{\displaystyle \scriptstyle V}
, právě když lze každý vektor z prostoru V{\displaystyle \scriptstyle V} vyjádřit jako lineární kombinaci vektorů z množiny X{\displaystyle \scriptstyle X}
vyjádřit jako lineární kombinaci vektorů z množiny X{\displaystyle \scriptstyle X} . Prvky množiny X{\displaystyle \scriptstyle X}
. Prvky množiny X{\displaystyle \scriptstyle X} pak nazýváme generátory vektorového prostoru V{\displaystyle \scriptstyle V}
pak nazýváme generátory vektorového prostoru V{\displaystyle \scriptstyle V} .
.
Lineární obal
Mějme vektorový prostor V{\displaystyle \scriptstyle V} nad tělesem T{\displaystyle \scriptstyle T}
nad tělesem T{\displaystyle \scriptstyle T} a množinu vektorů x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}}
a množinu vektorů x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}} pro jisté přirozené číslo n{\displaystyle \scriptstyle n}
pro jisté přirozené číslo n{\displaystyle \scriptstyle n} . Pak množinu všech lineárních kombinací těchto vektorů nazýváme jejich lineárním obalem (anglicky linear span, někdy též linear hull). Označíme-li lineární obal vektorů x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}}
. Pak množinu všech lineárních kombinací těchto vektorů nazýváme jejich lineárním obalem (anglicky linear span, někdy též linear hull). Označíme-li lineární obal vektorů x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}} jako {x→1,x→2,…,x→n}lin{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}}
jako {x→1,x→2,…,x→n}lin{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}} , můžeme ho matematicky vyjádřit jako množinu
, můžeme ho matematicky vyjádřit jako množinu
{x→1,x→2,…,x→n}lin={∑i=1nαix→i|(∀i∈{1,…,n})(αi∈T)},{\displaystyle \{{\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}=\left\{\sum _{i=1}^{n}\alpha _{i}{\vec {x}}_{i}{\Bigg |}(\forall i\in \{1,\ldots ,n\})(\alpha _{i}\in T)\right\},}
Vektory x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}} se pak nazývají generátory lineárního obalu, jim příslušného. Říkáme též, že vektory x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}}
se pak nazývají generátory lineárního obalu, jim příslušného. Říkáme též, že vektory x→1,x→2,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},{\vec {x}}_{2},\ldots ,{\vec {x}}_{n}} generují daný lineární obal, potažmo množinu.
generují daný lineární obal, potažmo množinu.
Báze
Báze vektorového prostoru V{\displaystyle \scriptstyle V} je takový lineárně nezávislý soubor vektorů x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}}
je takový lineárně nezávislý soubor vektorů x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}} , pro který platí rovnost V={x→1,…,x→n}lin{\displaystyle \scriptstyle V=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}}
, pro který platí rovnost V={x→1,…,x→n}lin{\displaystyle \scriptstyle V=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}} . Vektory x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}}
. Vektory x→1,…,x→n{\displaystyle \scriptstyle {\vec {x}}_{1},\ldots ,{\vec {x}}_{n}} pak nazýváme bazické vektory. V symbolech tedy
pak nazýváme bazické vektory. V symbolech tedy
vektory x→1,…,x→n tvoří bázi prostoru V⇔(x→1,…,x→n jsou lineárně nezávislé ∧ V={x→1,…,x→n}lin).{\displaystyle {\text{vektory }}{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}{\text{ tvoří bázi prostoru }}V\quad \Leftrightarrow \quad ({\vec {x}}_{1},\ldots ,{\vec {x}}_{n}{\text{ jsou lineárně nezávislé }}\wedge \ V=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{n}\}_{\text{lin}}).}
Důkaz
Proveďme důkaz neúplnou matematickou indukcí. Předpokládejme nejprve n≤m{\displaystyle \scriptstyle n\leq m} , poté ukážeme, že předpoklad n>m{\displaystyle \scriptstyle n>m}
, poté ukážeme, že předpoklad n>m{\displaystyle \scriptstyle n>m} vede ke sporu. Pro počáteční krok matematické indukce uvažujme množinu {x→1,y→1,…,y→m}{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}}
vede ke sporu. Pro počáteční krok matematické indukce uvažujme množinu {x→1,y→1,…,y→m}{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}} vzniklou tak, že k vektorům z množiny Y{\displaystyle \scriptstyle Y}
vzniklou tak, že k vektorům z množiny Y{\displaystyle \scriptstyle Y} přidáme jeden ("první") vektor z množiny X{\displaystyle \scriptstyle X}
přidáme jeden ("první") vektor z množiny X{\displaystyle \scriptstyle X} . O vektorech z množiny X{\displaystyle \scriptstyle X}
. O vektorech z množiny X{\displaystyle \scriptstyle X} ovšem víme, že je lze vyjádřit pomocí vektorů z Y{\displaystyle \scriptstyle Y}
ovšem víme, že je lze vyjádřit pomocí vektorů z Y{\displaystyle \scriptstyle Y} a námi sestrojená množina je tak lineárně závislá. Existuje v ní tedy vektor y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}}
a námi sestrojená množina je tak lineárně závislá. Existuje v ní tedy vektor y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}} pro jistý index i1∈{1,…,m}{\displaystyle \scriptstyle i_{1}\in \{1,\ldots ,m\}}
pro jistý index i1∈{1,…,m}{\displaystyle \scriptstyle i_{1}\in \{1,\ldots ,m\}} , který lze nakombinovat ze zbylých vektorů této množiny. Neboli
, který lze nakombinovat ze zbylých vektorů této množiny. Neboli
y→i1∈{x→1,y→1,…,y→i1−1,y→i1+1,…,y→m}lin,{\displaystyle {\vec {y}}_{i_{1}}\in \{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{i_{1}-1},{\vec {y}}_{i_{1}+1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}},}
kde symbol {…}lin{\displaystyle \scriptstyle \{\ldots \}_{\text{lin}}} značí lineární obal. Ačkoliv nám lineární závislost množiny vektorů zajišťuje, že v ní existuje vektor, který lze nakombinovat pomocí ostatních, mohli jsme s klidem vzít za tento vektor jeden z vektorů množiny Y{\displaystyle \scriptstyle Y}
značí lineární obal. Ačkoliv nám lineární závislost množiny vektorů zajišťuje, že v ní existuje vektor, který lze nakombinovat pomocí ostatních, mohli jsme s klidem vzít za tento vektor jeden z vektorů množiny Y{\displaystyle \scriptstyle Y} a ne opět vektor x→1{\displaystyle \scriptstyle {\vec {x}}_{1}}
a ne opět vektor x→1{\displaystyle \scriptstyle {\vec {x}}_{1}} . To, že je množina {x→1,y→1,…,y→m}{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}}
. To, že je množina {x→1,y→1,…,y→m}{\displaystyle \scriptstyle \{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}} lineárně závislá totiž znamená, že existuje netriviální lineární kombinace α0x→1+∑i=1mαiy→i{\displaystyle \scriptstyle \alpha _{0}{\vec {x}}_{1}+\sum _{i=1}^{m}\alpha _{i}{\vec {y}}_{i}}
lineárně závislá totiž znamená, že existuje netriviální lineární kombinace α0x→1+∑i=1mαiy→i{\displaystyle \scriptstyle \alpha _{0}{\vec {x}}_{1}+\sum _{i=1}^{m}\alpha _{i}{\vec {y}}_{i}} rovná nulovému vektoru. Kdyby α0≠0{\displaystyle \scriptstyle \alpha _{0}\neq 0}
rovná nulovému vektoru. Kdyby α0≠0{\displaystyle \scriptstyle \alpha _{0}\neq 0} a všechny ostatní koeficienty byly nulové, byl by to spor s lineární nezávislostí množiny X.{\displaystyle \scriptstyle X.}
a všechny ostatní koeficienty byly nulové, byl by to spor s lineární nezávislostí množiny X.{\displaystyle \scriptstyle X.} Existuje tedy nenulový koeficient αi1{\displaystyle \scriptstyle \alpha _{i_{1}}}
Existuje tedy nenulový koeficient αi1{\displaystyle \scriptstyle \alpha _{i_{1}}} , kde i1∈{1,…,m}{\displaystyle \scriptstyle i_{1}\in \{1,\ldots ,m\}}
, kde i1∈{1,…,m}{\displaystyle \scriptstyle i_{1}\in \{1,\ldots ,m\}} je jistý index vektoru z Y{\displaystyle \scriptstyle Y}
je jistý index vektoru z Y{\displaystyle \scriptstyle Y} . Tímto koeficientem můžeme dělit a vyjádřit dané y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}}
. Tímto koeficientem můžeme dělit a vyjádřit dané y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}} pomocí zbylých vektorů způsobem
pomocí zbylých vektorů způsobem
y→i1=1αi1(−α0x→1−∑i=1,i≠i1mαiy→i).{\displaystyle {\vec {y}}_{i_{1}}={\frac {1}{\alpha _{i_{1}}}}\left(-\alpha _{0}{\vec {x}}_{1}-\sum _{i=1,i\neq i_{1}}^{m}\alpha _{i}{\vec {y}}_{i}\right).}
Protože vektor x→1{\displaystyle \scriptstyle {\vec {x}}_{1}} lze nakombinovat z vektorů z Y{\displaystyle \scriptstyle Y}
lze nakombinovat z vektorů z Y{\displaystyle \scriptstyle Y} , je {Y}lin={x→1,y→1,…,y→m}lin{\displaystyle \scriptstyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}}}
, je {Y}lin={x→1,y→1,…,y→m}lin{\displaystyle \scriptstyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}}} . Obdobně pro y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}}
. Obdobně pro y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}} a máme tedy
a máme tedy
{Y}lin={x→1,y→1,…,y→i1−1,y→i1+1,…,y→m}lin,{\displaystyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},{\vec {y}}_{1},\ldots ,{\vec {y}}_{i_{1}-1},{\vec {y}}_{i_{1}+1},\ldots ,{\vec {y}}_{m}\}_{\text{lin}},}
viz (druhé) tvrzení v oddíle Ostatní v článku Lineární obal. Přikročme nyní k důkazu indukčního kroku. Předpokládejme, že pro všechna přirozená k≥1{\displaystyle \scriptstyle k\geq 1} , kde k<n{\displaystyle \scriptstyle k<n}
, kde k<n{\displaystyle \scriptstyle k<n} , existují navzájem různé indexy i1,…,im−k∈{1,…,m}{\displaystyle \scriptstyle i_{1},\ldots ,i_{m-k}\in \{1,\ldots ,m\}}
, existují navzájem různé indexy i1,…,im−k∈{1,…,m}{\displaystyle \scriptstyle i_{1},\ldots ,i_{m-k}\in \{1,\ldots ,m\}} tak, že
tak, že
{Y}lin={x→1,…,x→k,y→i1,…,y→im−k}lin.{\displaystyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k},{\vec {y}}_{i_{1}},\ldots ,{\vec {y}}_{i_{m-k}}\}_{\text{lin}}.}
Neboť z předpokladů věty platí, že x→k+1∈{Y}lin{\displaystyle \scriptstyle {\vec {x}}_{k+1}\in \{Y\}_{\text{lin}}} , je množina {x→1,…,x→k,x→k+1,y→i1,…,y→im−k}{\displaystyle \scriptstyle \{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k},{\vec {x}}_{k+1},{\vec {y}}_{i_{1}},\ldots ,{\vec {y}}_{i_{m-k}}\}}
, je množina {x→1,…,x→k,x→k+1,y→i1,…,y→im−k}{\displaystyle \scriptstyle \{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k},{\vec {x}}_{k+1},{\vec {y}}_{i_{1}},\ldots ,{\vec {y}}_{i_{m-k}}\}} lineárně závislá, přičemž množina {x→1,…,x→k+1}{\displaystyle \scriptstyle \{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k+1}\}}
lineárně závislá, přičemž množina {x→1,…,x→k+1}{\displaystyle \scriptstyle \{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k+1}\}} je lineárně nezávislá. V první jmenované množině tedy existuje vektor y→ip{\displaystyle \scriptstyle {\vec {y}}_{i_{p}}}
je lineárně nezávislá. V první jmenované množině tedy existuje vektor y→ip{\displaystyle \scriptstyle {\vec {y}}_{i_{p}}} pro jisté ip∈{1,…,m}{\displaystyle \scriptstyle i_{p}\in \{1,\ldots ,m\}}
pro jisté ip∈{1,…,m}{\displaystyle \scriptstyle i_{p}\in \{1,\ldots ,m\}} (kde p∈{1,…,m−k}{\displaystyle \scriptstyle p\in \{1,\ldots ,m-k\}}
(kde p∈{1,…,m−k}{\displaystyle \scriptstyle p\in \{1,\ldots ,m-k\}} ), který lze vyjádřit pomocí zbylých vektorů. Postupem obdobným tomu pro y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}}
), který lze vyjádřit pomocí zbylých vektorů. Postupem obdobným tomu pro y→i1{\displaystyle \scriptstyle {\vec {y}}_{i_{1}}} dospíváme k rovnosti
dospíváme k rovnosti
{Y}lin={x→1,…,x→k,x→k+1,y→i1,…,y→ip−1,y→ip+1,…,y→im−k}lin.{\displaystyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k},{\vec {x}}_{k+1},{\vec {y}}_{i_{1}},\ldots ,{\vec {y}}_{i_{p}-1},{\vec {y}}_{i_{p}+1},\ldots ,{\vec {y}}_{i_{m-k}}\}_{\text{lin}}.}
Přeznačíme-li indexy u vektorů v předchozím vzorci, dostáváme vztah
{Y}lin={x→1,…,x→k,x→k+1,y→j1,…,y→jm−k−1}lin,{\displaystyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{k},{\vec {x}}_{k+1},{\vec {y}}_{j_{1}},\ldots ,{\vec {y}}_{j_{m-k-1}}\}_{\text{lin}},}
který dokončuje indukční krok. Pro případ n≤m{\displaystyle \scriptstyle n\leq m} máme tedy větu dokázánu. Předpokládejme nyní, že n>m{\displaystyle \scriptstyle n>m}
máme tedy větu dokázánu. Předpokládejme nyní, že n>m{\displaystyle \scriptstyle n>m} . Kdybychom postupovali postupem stejným jako výše, tak bychom se dostali postupným přidáváním vektorů k původnímu lineárnímu obalu do stavu, kdy chceme přidat vektor x→m+1{\displaystyle \scriptstyle {\vec {x}}_{m+1}}
. Kdybychom postupovali postupem stejným jako výše, tak bychom se dostali postupným přidáváním vektorů k původnímu lineárnímu obalu do stavu, kdy chceme přidat vektor x→m+1{\displaystyle \scriptstyle {\vec {x}}_{m+1}} , nemáme už ale žádný zbylý vektor z Y{\displaystyle \scriptstyle Y}
, nemáme už ale žádný zbylý vektor z Y{\displaystyle \scriptstyle Y} , za který bychom ho mohli vyměnit. Neboli bychom měli
, za který bychom ho mohli vyměnit. Neboli bychom měli
{Y}lin={x→1,…,x→m}lin.{\displaystyle \{Y\}_{\text{lin}}=\{{\vec {x}}_{1},\ldots ,{\vec {x}}_{m}\}_{\text{lin}}.}
Z předpokladů věty ale x→m+1∈{Y}lin{\displaystyle \scriptstyle {\vec {x}}_{m+1}\in \{Y\}_{\text{lin}}} a podle rovnosti výše můžeme tento vektor vyjádřit pomocí zbylých vektorů z množiny X{\displaystyle \scriptstyle X}
a podle rovnosti výše můžeme tento vektor vyjádřit pomocí zbylých vektorů z množiny X{\displaystyle \scriptstyle X} . To je ale spor s lineární nezávislostí množiny X{\displaystyle \scriptstyle X}
. To je ale spor s lineární nezávislostí množiny X{\displaystyle \scriptstyle X} , což dokončuje důkaz věty.
, což dokončuje důkaz věty.
typu
platí
,
představuje nejmenší hodnotu z množiny
. Hodnost matice typu
je tedy menší nebo rovna menšímu z čísel
.
, která má na hlavní diagonále jedničky a na ostatních místech nuly. Jednotková matice se značí In, případně jen I, je-li velikost nepodstatná nebo lze-li ji odvodit z kontextu
vzájemnou výměnou řádků a sloupců, označujeme jako transponovanou matici a značíme
. Pro jednotlivé prvky transponované matice platí
.
rozměry
, pak její transpozicí vznikne matice o rozměrech
.
.
a
. Pak složené zobrazení BA definované vztahem
je lineární, tj.
.
a libovolné vektory
. Pak
, což je ekvivalentní linearitě složeného zobrazení.
. Zobrazení
z prostoru X do prostoru Y, tj.
, se nazývá lineární zobrazení, právě když pro libovolné vektory
a pro libovolný prvek
z tělesa
toto zobrazení splňuje následující dvě podmínky:
při lineárním zobrazení
se značí
. Často se ale pro jednoduchost závorky vypouští a píše se jen
. Podobně obraz množiny
se značí
.
konečné dimenze n. Existuje v něm tedy n-členná báze
a každý vektor
tohoto prostoru lze vyjádřit jako vhodnou lineární kombinaci
. Využijeme-li nyní linearity zobrazení A, dostáváme
lze tedy vyjádřit jako nějakou lineární kombinaci vektorů
, kde koeficienty jsou totožné s koeficienty u vzoru
. Celou informaci o struktuře zobrazení A lze tak získat pouze ze znalosti toho, jak působí na bazické vektory. Rozvinutím právě uvedené myšlenky pak dospíváme k definici matice lineárního zobrazení, jak je uvedeno níže.
(jedná se o zkratku ze slova kernel, anglického označení pro jádro). Přesněji: Mějme dva vektorové prostory X a Y nad stejným tělesem
. Dále nechť A je lineární zobrazení z X do Y, tj.
. Pak jádro zobrazení A je množina
označuje nulový vektor v prostoru Y. Dimenze jádra zobrazení A, tj.
, se občas označuje jako defekt zobrazení A. Z vlastností v oddíle Nulový vektor je vidět, že nulový vektor leží v jádře každého lineárního zobrazení. Dokonce lze dokázat následující tvrzení: Lineární zobrazení je prosté právě tehdy, když v jeho jádru leží pouze nulový vektor (důkaz viz Prostota zobrazení). Neboť množina
je také vektorový (pod)prostor, tak lze využít tvrzení z oddílu Obrazy a vzory vektorů a jejich podprostorů o vzoru podprostoru abychom uviděli, že jádro zobrazení je vektorový podprostor, tj.
, zbývá ověřit její linearitu. Označme si
,
, kde vektory
jsme si vybrali libovolně. Z linearity zobrazení A plyne
. Zobrazení A tedy vektoru
přiřadilo vektor
. Jeho inverze tedy učiní opak dostávajíc
. Když si rozepíšeme, jak vznikly vektory
a
dospíváme k výrazu
, což je ekvivalentní s linearitou zobrazení
.
, kde oba vektorové prostory jsou konečných dimenzí,
. V obou prostorech tedy existuje jejich báze, označme bazické vektory prostoru X jako
a podobně nechť
je báze prostoru Y. Libovolný vektor
z prostoru X lze tedy zapsat jako lineární kombinaci bazických vektorů
dostáváme vektor
, pro nějž platí
leží v prostoru Y, takže je lze vyjádřit jako lineární kombinace bazických vektorů
ve tvaru
tak máme
, pro vektor
máme
, pro vektor
máme
atd. Celkově tedy
v tomto výrazu pocházejí z lineární kombinace pro vstupní vektor
a vektory
jsou předem zadaná báze prostoru Y. Jediné, co tedy charakterizuje zobrazení A samotné jsou tak prvky
. Tyto si můžeme uspořádat do matice tvaru
a
, kde jsme označili bázi prostoru X jako
a bázi prostoru Y jako
. Tato matice plně popisuje strukturu lineárního zobrazení A. Značí se symbolem
.
,
.
-tého řádku je alespoň takový jako počet nul na začátku
-tého řádku). [1]
be a field. The column space of an m × n matrix with components from
is a linear subspace of the m-space
. The dimension of the column space is called the rank of the matrix and is at most min(m, n).[1] A definition for matrices over a ring
is also possible.
and
respectively.
jsou lineárně závislé, právě když platí
jsou definovány relace
a na množině
jsou definovány relace
. Řekneme, že zobrazení
je izomorfismus mezi
a
vzhledem k relacím
a
, pokud platí:
a
jsou izomorfní, pokud mezi nimi existuje nějaký izomorfismus ve smyslu výše uvedené definice.
a
jsou dvě báze, pro které platí
, neboli
se nazývá matice přechodu od báze
k bázi
. Pro souřadnice pak platí
jsou souřadnice libovolného vektoru v bázi
a
jsou jeho souřadnice v bázi
a
je inverzní matice k matici
.
nad tělesem
. Dále nechť
je nějaký vektor a
je soubor
vektorů z prostoru
. Pak říkáme, že vektor
je lineární kombinací (angl. linear combination) vektorů
, právě když existuje
-tice čísel z tělesa
taková, že lze vektor
vyjádřit ve tvaru sumy
nad tělesem
. Dále buď
neprázdná podmnožina prostoru
, která splňuje
nazýváme podprostorem vektorového prostoru
a značíme
.
či
pro nějaké přirozené číslo n, tak se jeho prvky nazývají aritmetické vektory. Počet složek vektoru je roven dimenzi vektorového prostoru.
je vektorový prostor a uvažujme podmnožinu množiny přirozených čísel, kterou označíme
a definujeme vztahem
neprázdná, tak říkáme, že vektorový prostor
má konečnou dimenzi, která je rovna číslu
. Značíme,
prázdná, tj.
, tak říkáme, že vektorový prostor
má nekonečnou dimenzi a píšeme
, kde
, jsou absolutní členy soustavy (nebo také tzv. pravá strana soustavy). V obecném případě mohou být koeficienty i absolutní členy komplexními čísly.
je vektorový prostor nad tělesem
s vektorovými operacemi
, právě když je množina
uzavřená na operace
a
a současně platí tzv. axiomy vektorového prostoru. Těchto axiomů je osm a jejich znění je následující:
vektorový prostor nad tělesem
a mějme dále soubor vektorů
pro jisté přirozené číslo
. Uvažujme pak všechny možné lineární kombinace tohoto souboru vektorů, které jsou rovny nulovému vektoru. Pak říkáme, že soubor
je lineárně nezávislý, právě když ze všech lineárních kombinací těchto vektorů je rovna nulovému vektoru jen triviální lineární kombinace. V opačném případě nazýváme soubor výše lineárně závislý.
, kde
je množina a + (sčítání) a
(násobení) jsou binární operace, nazveme tělesem, je-li
okruh a platí-li navíc
spolu s binární operací na ní, která se nazývá grupová operace. Tato operace libovolným dvěma prvkům grupy
přiřazuje prvek téže grupy
. Značení grupové operace se v literatuře liší. Obvykle se značí jako násobení
, resp. jenom
, v Abelových grupách často jako sčítání
, a někdy také pomocí dalších symbolů (
, resp.
). Podle kontextu říkáme, že
je složení, resp. součin, resp. součet prvků
a
. Dále se v definici grupy požaduje, aby grupová operace splňovala určité vlastnosti, které se nazývají axiomy grupy.[1]
v
je i složení
prvkem
.[pozn 1]
grupy
platí
, tj. výsledek složení tří prvků nezávisí na umístění závorek.[pozn 2] Díky tomu má smysl psát složení tří a více prvků
i bez závorek.
takový, že pro všechna
platí
. Tento prvek se nazývá neutrální prvek anebo jednotkový prvek a značí se také
, resp.
.[pozn 3]
existuje prvek
takový, že
, tj. jejich složení v libovolném pořadí je rovno neutrálnímu prvku
. Prvek
se také nazývá inverzní prvek k
a značí se
. Lze ukázat, že neutrální prvek je v grupě jenom jeden a že inverzní prvek k
je dán jednoznačně.
. Grupa, ve které tato rovnost platí pro všechna
, se nazývá komutativní grupa nebo také Abelova grupa.
a
jsou dvě množiny vektorů z vektorového prostoru
. Nechť jsou dále vektory z množiny
lineárně nezávislé a každý z nich lze vyjádřit jako lineární kombinaci vektorů z množiny
. Pak platí, že
. Pokud
, tak je lineární obal množiny
nutně roven lineárnímu obalu množiny
. Neboli
. (Výraz
značí lineární obal množiny
atd.). Dále, pokud platí ostrá nerovnost
, tak existují navzájem různé indexy
takové, že
a dále jeho jistou neprázdnou podmnožinu
. Pak říkáme, že množina
generuje vektorový prostor
, právě když lze každý vektor z prostoru
vyjádřit jako lineární kombinaci vektorů z množiny
. Prvky množiny
pak nazýváme generátory vektorového prostoru
.
nad tělesem
a množinu vektorů
pro jisté přirozené číslo
. Pak množinu všech lineárních kombinací těchto vektorů nazýváme jejich lineárním obalem (anglicky linear span, někdy též linear hull). Označíme-li lineární obal vektorů
jako
, můžeme ho matematicky vyjádřit jako množinu
se pak nazývají generátory lineárního obalu, jim příslušného. Říkáme též, že vektory
generují daný lineární obal, potažmo množinu.
je takový lineárně nezávislý soubor vektorů
, pro který platí rovnost
. Vektory
pak nazýváme bazické vektory. V symbolech tedy
, poté ukážeme, že předpoklad
vede ke sporu. Pro počáteční krok matematické indukce uvažujme množinu
vzniklou tak, že k vektorům z množiny
přidáme jeden ("první") vektor z množiny
. O vektorech z množiny
ovšem víme, že je lze vyjádřit pomocí vektorů z
a námi sestrojená množina je tak lineárně závislá. Existuje v ní tedy vektor
pro jistý index
, který lze nakombinovat ze zbylých vektorů této množiny. Neboli
značí lineární obal. Ačkoliv nám lineární závislost množiny vektorů zajišťuje, že v ní existuje vektor, který lze nakombinovat pomocí ostatních, mohli jsme s klidem vzít za tento vektor jeden z vektorů množiny
a ne opět vektor
. To, že je množina
lineárně závislá totiž znamená, že existuje netriviální lineární kombinace
rovná nulovému vektoru. Kdyby
a všechny ostatní koeficienty byly nulové, byl by to spor s lineární nezávislostí množiny
Existuje tedy nenulový koeficient
, kde
je jistý index vektoru z
. Tímto koeficientem můžeme dělit a vyjádřit dané
pomocí zbylých vektorů způsobem
lze nakombinovat z vektorů z
, je
. Obdobně pro
a máme tedy
, kde
, existují navzájem různé indexy
tak, že
, je množina
lineárně závislá, přičemž množina
je lineárně nezávislá. V první jmenované množině tedy existuje vektor
pro jisté
(kde
), který lze vyjádřit pomocí zbylých vektorů. Postupem obdobným tomu pro
dospíváme k rovnosti
máme tedy větu dokázánu. Předpokládejme nyní, že
. Kdybychom postupovali postupem stejným jako výše, tak bychom se dostali postupným přidáváním vektorů k původnímu lineárnímu obalu do stavu, kdy chceme přidat vektor
, nemáme už ale žádný zbylý vektor z
, za který bychom ho mohli vyměnit. Neboli bychom měli
a podle rovnosti výše můžeme tento vektor vyjádřit pomocí zbylých vektorů z množiny
. To je ale spor s lineární nezávislostí množiny
, což dokončuje důkaz věty.