Lineární algebra

Created by Pavel Klavík

OrgPage Lineární algebra

Autor: Pavel Klavík
Poslední změna: 24.11.2016

Poděkování: Zdeněk Hedrlín, Peter Zeman, studenti pokročilých cvičení.

V současné chvíli jsou tato hlavní témata:

• Soustavy lineárních rovnic Ax=b.
• Matice.
• Vektorové prostory.
• Lineární zobrazení (homomorfismy).

Následující témata jsou rozpracovaná:

• Skalární součin, norma, ortogonalita.
• Determinanty.
• Vlastní čísla.
• Kvadratické formy a definitnost.

Asociace, kde je to nutné, jsou popsány v jednotlivých oknech. Pro důležité asociace je vytvořeno speciální okno mezi pojmy, například pro maticovou reprezentaci lineárního zobrazení.

Zdroje

Obsah je utvořen podle výuky na Pokročilých cvičeních z Lineární algebry a knih Povídání o lineární algebře a Lineární algebra II: Pokročilé cvičení (převzaty skoro všechny obrázky).

Grupy

Matematická struktura 𝔾 spolu s binární operací ∘ : 𝔾 ⨯ 𝔾 → 𝔾 se nazývá grupa, pokud splňuje následující vlastnosti:

• Platí asociativita: a∘(b∘c) = (a∘b)∘c.
• Existuje neutrální prvek e, že a∘e = e∘a = a.
• Existují inverzní prvky a^-1, že a∘a^-1 = a^-1∘a = e.

Čísla typicky tvoří grupu, například ℤ je grupa pro sčítání. Struktura ℤ_n tvořená prvky {0,1,...,n-1}, s operací sčítání modulo n je grupa. Tyto grupy jsou však značně speciální, typická grupa je nekomutativní.

Cayley vymyslel v 1878 způsob, jak vizualizovat grupy pomocí diagramů. Vrcholy jsou jednotlivé prvky grupy 𝔾. Hrany popisují množinu generátorů g₁, ..., g_k, pro kterou

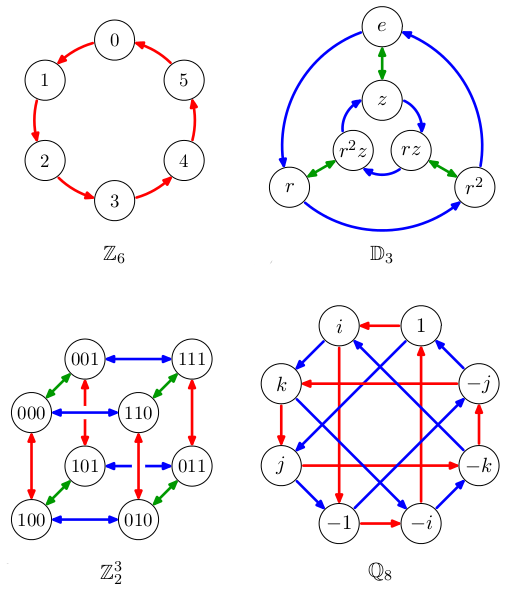
⟨g₁, ..., g_k⟩ = 𝔾.
Jednotlivým generátorům přiřadíme barvy a i-tou barvou nakreslíme šipky z x do g_i∘x. Tím je zachycena struktura celé grupy a je to mnohem přehlednější než popisovat binární operaci ∘ tabulkou.

Grupy vlevo jsou komutativní: grupa sčítání modulo 6 a grupa binárních vektorů. Grupy vpravo však komutativní nejsou, například pro 𝔻₃ je modrá šipka následovaná zelenou něco jiného než naopak. Grupa 𝔻₃ je grupa symetrických transformací rovnostranného trojúhelníka, kde operace ∘ je skládání. Grupa ℚ₈ je grupa imaginárních jednotek kvaternionů (zobecnění komplexních čísel) a operace popisuje jejich násobení.

Lineární (ne)závislost

Vektor u je v množině X nadbytečný, pokud ⟨X \ {u}⟩ = ⟨X⟩. Nadbytečné vektory můžeme z množiny postupně odebírat a nezmění se její lineární obal. Motivace je, že chceme lineární obal ⟨X⟩ popsat pomocí co nejmenší množiny vektorů.

Uvažme rovinu vzniklou jako lineární obal tří vektorů. Libovolný z nich je nadbytečný, jeho odebráním se obal nezmění. Po odebrání nejsou již zbývající dva vektory nadbytečné.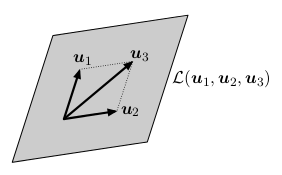
Povšimněme si, že počátek 0 je vždy nadbytečný.

Množina vektorů X je lineárně závislá, pokud obsahuje nadbytečný vektor, a lineárně nezávislá jinak.

Tvrzení: Následující definice lineární závislosti x₁,...,x_n jsou ekvivalentní:

1. Obsahuje nadbytečný vektor.
2. Existuje vektor x_i, který je lineární kombinací zbývajících.
3. Existuje netriviální lineární kombinace nuly: 0 = c₁*x₁ + ... + c_n*x_n, že alespoň jeden z koeficientů c_i je nenulový.
4. Existuje vektor v lineárním obalu, který lze vyjádřit jako dvě různé lineární kombinace.

Tagy: #klicove

Algebraická tělesa

I když jsme skoro celou lineární algebru popisovali nad reálnými čísly ℝ. Avšak celou řadu speciálních vlastností ℝ jsme nikdy nepoužili. Například pro řešení soustavy lineárních rovnic Gaussovou eliminací nepotřebujeme vědět, že existují odmocniny nebo limity Cauchyovských posloupností. Můžeme proto místo ℝ použít libovolnou matematickou strukturu čísel zvanou algebraické těleso, která splňuje několik pravidel.

Definice algebraického tělesa. Matematická struktura 𝕋 spolu s dvěma binárními operacemi sčítání + : 𝕋 ⨯ 𝕋 → 𝕋 a násobení * : 𝕋 ⨯ 𝕋 → 𝕋 se nazývá těleso, pokud splňuje následující vlastnosti:

• 𝕋 je vzhledem k operaci sčítání grupa a označme 0 její neutrální prvek.
• 𝕋 ∖ {0} je grupa vzhledem k operaci násobení, jejíž neutrální prvek označme 1.
• Platí distributivita: a*(b+c) = a*b+a*c.

Tedy těleso jsou dvě grupy svázané distributivitou.

Příklady těles. Vyjma ℝ jsou standardní příklady nekonečných těles komplexní čísla ℂ a racionální čísla ℚ. Existují i konečná tělesa, která jsou dokonce přesně charakterizovaná.

Zobecnění vektorových prostorů. Ve většině diagramu se uvažují vektorové prostory nad tělesem reálných čísel ℝ, tedy prostory ℝⁿ. Je však možné uvažovat prostory nad libovolným tělesem 𝕋. V konkrétní definici dostáváme prostory 𝕋ⁿ, v abstraktní defici jsou skaláry z 𝕋 místo ℝ. Také matice se uvažují nad tělesem 𝕋 jako 𝕋^{m x n}. Například v informatice je užitečný prostor binárních vektorů ℤ₂ⁿ.

Velká část výsledků lineární algebry popisovaných v tomto diagramu funguje bez jakékoliv změny pro vektorové prostory nad obecnými tělesy 𝕋. V následujících částech jsou odlišnosti:

• Nemusí platit nezávislost fundamentálních podprostorů, jediný možný důkaz musí využívat ortogonalitu. Například matice A = (1,1) nad ℤ₂ má R(A) = Ker(A).
• Standardní skalární součin lze uvažovat, ale nemusí splňovat pozitivní definitnost.
• Norma proto nedává smysl a ortogonalita se chová velice odlišně: nenulový vektor může být kolmý sám k sobě, například (1,1) nad ℤ₂.
• Vlastní čísla nemusí existovat, protože polynom nad jiným tělesem než ℂ nemusí mít kořeny.
• Definitnost matic nedává smysl, protože nad tělesem nemusí existovat uspořádání.

Steinitzova věta o výměně

Věta: Nechť X je libovolná množina vektorů a Y je lineárně nezávislá množina vektorů z ⟨X⟩. Potom existuje Z ⊆ X, že |Z|=|Y| taková, že
⟨X \ Z ∪ Y⟩ = ⟨X⟩.
Tato věta má řadu zajímavých důsledků:

• Vektorový prostor obsahuje spoustu bází a na jejich vektorech není nic speciálního.
• Libovolnou lineárně nezávislou množinu lze rozšířit na bázi.
• Vždy platí, že |X| ≥ |Y|. Proto každá lineárně nezávislá množina má velikost menší či rovnou libovolnému generátoru, a všechny báze jsou stejně velké.

Důkaz: Nechť Y = {y₁,...,y_n}. Postupně vkládáme vektory Y jeden za druhým do X za pomocí lemmatu o výměně. Problém by však mohl být, že při vložení y_i by lemma mohlo vyjmout předtím vložené y_j.

Uvědomme si však, že v lemmatu o výměně můžeme zvolit jako z libovolné x_k takové, že koeficient 𝛼_k ≠ 0. Proto vždy při vkládání y_i vyjmeme některý z vektorů X. Pokud by to nebylo možné, dostáváme, že y_i je lineární kombinace ostatních vektorů z Y, což je spor s lineární nezávislostí Y.

Tagy: #klicove

Konečná tělesa

Konečné těleso je tvořeno konečně mnoha prvky a nazývá se Galoisovo těleso, značeno GF(n) pro n prvků. S konečnými tělesy se dobře pracuje v počítačích a mají třeba řadu aplikací v kryptografii a teorii kódování.

Nejjednodušší příklady těles jsou prvočíselné velikosti:

Tvrzení: Struktura ℤ_n je tvořena prvky {0,1,...,n-1}, s operacemi sčítání a násobení definovanými modulo n. Struktura ℤ_n je těleso, právě když n je prvočíslo p.

Důkaz: Pokud n není prvočíslo, je snadné ukázat, že neexistují inverzní prvky pro násobení. Existují 1 < a,b < n takové, že a*b = n. Tedy a*b = 0 v ℤ_n, což není v tělese možné.

Obtížnější je dokázat, že existují inverzní prvky pro násobení v ℤ_p. Stačí ukázat, že násobení k je bijekce na ℤ_p.

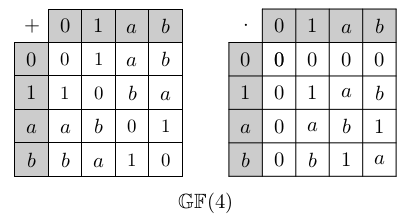
Složitější konečná tělesa však existují i pro jiné velikosti, například GF(4) vpravo.

Věta: Každé konečné těleso je řádu p^k, kde p je nějaké prvočíslo a k je přirozené číslo. Navíc pro každé p^k těleso vždy existuje a je určené jednoznačně až na izomorfismus, tedy značení GF(p^k) dává smysl.

Náznak důkazu: Mějme konečné těleso 𝕋, chceme dokázat, že jeho velikost je p^k. Charakteristika 𝕋 je nejmenší počet jedniček, který se sečte na nulu, a vždy je to prvočíslo p. Tyto součty jedniček tvoří podtěleso izomorfní ℤ_p. Hlavní trik je, že 𝕋 tvoří vektorový prostor nad tělesem ℤ_p. Ten má nějakou dimenzi k, a proto obsahuje p^k prvků.

Jednoznačnost tělesa velikosti p^k vyplývá z věty o izomorfismu. Konstrukce takového tělesa je složitější a postupuje se přes okruhy polynomů a jejich rozkladová tělesa, detaily vynecháme.

Dimenze

Dimenze vektorového prostoru či jeho podprostoru je velikost libovolné jeho báze. Pro vektorový prostor V se dimenze značí dim(V).

To, že je dimenze dobře definována, vyplývá ze Steinitzovy věty o výměně. Mějme dvě libovolné báze X a Y. Můžeme vektory báze X vyměnit za vektory báze Y a naopak, proto musí mít stejně prvků.

Pozorování: Pokud U je podprostor V, potom dim(U) ≤ dim(V).

Tagy: #klicove

Konstrukce báze

Celá teorie bází by byla nezajímavá, pokud by žádná báze neexistovala. Dokážeme si s následujícím předpokladem, že báze vždycky existuje (a dokonce je spousta způsobů, jak je zvolit).

Předpoklad: Vektorový prostor má konečnou dimenzi, tedy libovolná báze má konečnou velikost. (Dokonce podle Steinitzovy věty by stačilo, že existuje báze konečné velikosti.)

Bez předpokladu bychom museli uvažovat i nekonečně dimenzionální vektorové prostory (třeba prostory funkcí nebo posloupností), pro než jsou potřeba nekonečné báze. Myšlenkově to funguje totožně, ale je s tím řada technických problémů, například musíme uvažovat nekonečné lineární kombinace.

Nefungující nápad: odebírání z generátoru. Začneme s libovolným generátorem vektorového prostoru (například celým vektorovým prostorem U) a budeme z něj postupně odebírat nadbytečné vektory. Skončíme s lineárně nezávislým generátorem, neboli bází.

Problém je, že typicky bude generátor nekonečný i v konečně dimenzionálním vektorovém prostoru. Odebíráme nekonečně mnoho vektorů, navíc můžeme skončit s prázdnou množinou (problém nekonečna). Například v ℝ postupně odebereme všechny vektory přímky, protože každý bude nadbytečný vůči zbývajícím.

Fungující nápad: přidávání vektorů. Půjdeme na to proto obráceně, začneme s prázdnou množinou a budeme do ní postupně přidávat vektory při zachování lineární nezávislosti.

Nechť Y₀ = ∅ a Y_k je zkonstruovaná nezávislá množina s k vektory. Skončíme, pokud ⟨Y_k⟩ je celý prostor U. Jinak zvolíme libovolný vektor y_k+1 ∊ U ∖ ⟨Y_k⟩ a pokračujeme dál. Postup skončí po konečně mnoha krocích kvůli předpokladu a zkonstruuje bázi U.

Afinní podprostory

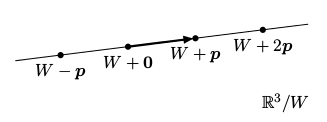
Afinní podprostory jsou zobecněním vektorových podprostorů. Afinní podprostor W+p vznikne z vektorového podprostoru W posunutím z počátku o vektor p:

Navíc uvažujeme i prázdnou množinu jako afinní podprostor. Například afinní podprostory ℝ³ jsou prázdná množina, všechny body, všechny přímky, všechny roviny a celý prostor.

Tvrzení: Platí, že W+p = W+q, právě když p-q ∊ W.

Důkaz: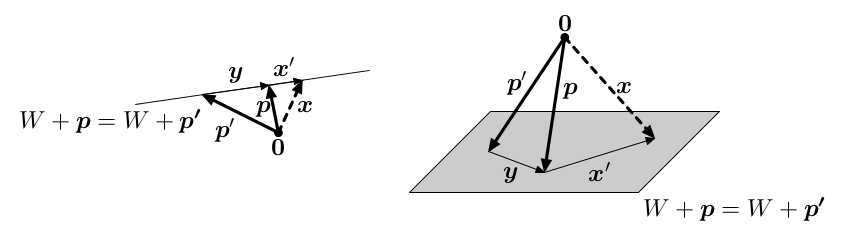
Navíc W+0 = W, tedy W+p = W, právě když p ∊ W.

Afinní podprostory jsou velice zajímavé strukturálně, více informací u faktorprostorů.

Tagy: #klicove

Vlastnosti vektorů ℝ n

Pokud pracujeme s abstraktní definicí vektorového prostoru, máme zaručeno několik vlastností vektorů: sčítání vektorů je komutativní, asociativní, platí distributivity s násobením, existuje nulový vektor, atd.

Pokud použijeme konstruktivní definici ℝⁿ, můžeme snadno dokázat, že vektory také splňují všechny tyto vlastnosti. Například nulový vektor je počátek 0 = (0,...,0).

Ukažme si myšlenku alespoň na jednom příkladu.

Tvrzení: Sčítání vektorů je komutativní, tedy platí u+v = v+u.

Důkaz: Nejprve si uvědomme, že vektory u+v a v+u jsou si rovny, právě když se shodují v každém koeficientu. A protože tyto koeficienty jsou reálná čísla, přenesou se jejich komutativita i na vektory:

Tento důkaz ilustruje obecný princip algebry. Matematické struktury jsou definovány tak, že jsou složeny z jednodušších struktur spolu s přidanými operacemi a vztahy. Pochopitelně tento řetěz někdy musí skončit, tedy nějakou základní strukturu musíme přímo popsat. Situace je podobná jako s ruskými panenkami Matrjoška.

Důležité je, že vlastnosti jednodušších struktur se přenášejí o hladinu výše na strukturu, která je obsahuje. Například vektory jsou tvořeny reálnými čísly, které vzniknou z podmnožin racionálních čísel, které vzniknou z dvojic celých čísel, které vzniknou jako dvě kopie přirozených čísel. Tedy to, že vektory jsou komutativní je důsledek toho, že přirozená čísla jsou komutativní.

Lemma o výměně

Jednodušší verze Steinitzovy věty. Říká, že je možné nahradit jeden vektor množiny za libovolný nenulový vektor z jejího lineárního obalu.

Lemma: Nechť X je libovolná množina vektorů a y ≠ 0 patří do ⟨X⟩. Potom existuje z∊X takové, že
⟨X \ {z} ∪ {y}⟩ = ⟨X⟩.

Důkaz: Protože y patří do ⟨X⟩, platí následující:
Proto ⟨X⟩ = ⟨X ∪ {y}⟩ ⊇ ⟨X \ {z} ∪ {y}⟩. Pro druhou inkluzi zvolíme jako z libovolný vektor x_i, jehož 𝛼_i ≠ 0. Snadnou úpravou ukážeme, že x_i lze vyjádřit pomocí ostatních x_j a y: Tedy ⟨X⟩ ⊆ ⟨X \ {x_i} ∪ {y}⟩.

Faktorprostory

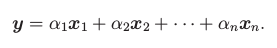
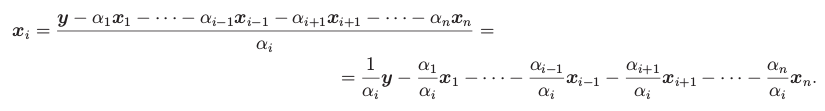
Afinní podprostory jsou zajímavé strukturálně.

Tvrzení: Množina všech afinní podprostorů vzniklých posunutím W tvoří vektorový prostor.

Důkaz: Stačí definovat vektorové operace: (W+p)+(W+q) = W+(p+q) a c*(W+p) = W+c*p. Rozmyslete si, že splňují definice vektorového prostoru.

Tyto vektorové prostory jsou důležité a říká se jim faktorprostory. Nechť V je vektorový prostor a W je jeho podprostor. Vektorový prostor všech afinních podprostorů vzniklých posunutím W se značí V/W a nazývá se faktorprostor nebo také kvocient.

Faktorprostor V/W si můžeme představit tak, že ve V "splácneme" každý afinní podprostor vzniklý posunutím W do jednoho vektoru.

Tvrzení: Platí, že dim(W)+dim(V/W) = dim(V).

Lineární obal a generátory

Lineární obal ⟨X⟩ množiny vektorů X je množina všech lineárních kombinací vektorů z X. Podle lemmatu jsou to všechny vektory, které lze získat z X aplikováním konečných posloupností operací. Lineární obal se někdy také značí L(X) nebo span(X). Říkáme, že X generuje ⟨X⟩.

Pozorování: Lineární obal ⟨X⟩ je vektorový podprostor.

Tvrzení: Lineární obal ⟨X⟩ je nejmenší vektorový podprostor, který obsahuje všechny vektory z X, což je infimum ve svazu podprostorů. Tedy ⟨X⟩ je průnik přes všechny vektorové podprostory, které obsahují X.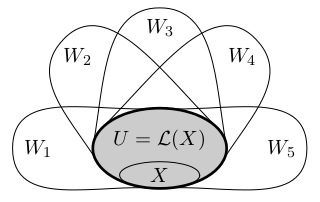
Tagy: #klicove

Báze

Množina vektorů se nazývá báze, pokud je lineárně nezávislá a generuje celý prostor. Chceme tedy co nejméně vektorů, které umožnují popsat vektorový prostor. Podobně můžeme báze uvažovat i pro libovolný vektorový podprostor.

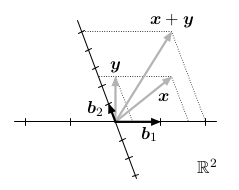
Každá báze b₁,...,b_n definuje systém souřadnic nad vektorovým prostorem:

Pokud x = c₁*b₁ + ... + c_n*b_n, jsou jeho souřadnice (c₁,...,c_n).
Různé báze definují různé systémy souřadnic. Například pro kanonickou bázi vlevo jsou souřadnice vektoru x rovny (5/2,2), zatímco pro bázi vpravo jsou (8/5,5/2). Následující vlastnost vyplývá z lineární nezávislosti báze:

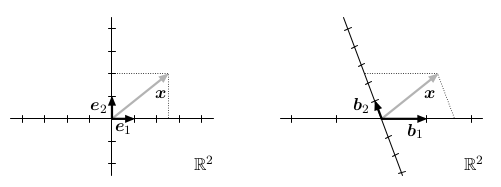
Tvrzení: Pro každý vektor x jsou jeho souřadnice určené jednoznačně.

Tagy: #klicove

Motivace pro různé báze

Je přirozené se ptát, proč chceme uvažovat různé báze a nevystačíme si s přirozenou kanonickou bází:

• Pro ℝⁿ je přirozené uvažovat kanonickou bázi, protože má speciální roli z pohledu složek vektorů (proto se nazývá kanonická). Avšak pro abstaktní vektorový prostor V žádná přirozená kanonická báze neexistuje. Bází je spousta a není žádná speciální, kterou bychom chtěli vždy zvolit. Tedy je lepší pracovat s teorii obecných bází.
• Řada problémů se mnohem zjednodušší při vhodné volbě báze. Lineární zobrazení je reprezentováno různými maticemi pro různé volby bází. Jedna z klíčových otázek lineární algebry je, jako bázi zvolit, aby byla reprezentující matice co nejjednodušší, což vede na vlastní čísla a třeba dekompozici podle singulárních hodnot SVD. Další příklad je Lagrangeova interpolace.
• Často hledáme vhodnou bázi, která je co nejlepší k popisu dané situace. Například ve statistice můžeme mít data jako vektory v hodně rozměrném prostoru. Hledáme bázi, ve které by bylo možné popsat data co nejjednodušším způsobem, například by se mohlo stát, že skoro všechna leží v nějaké rovině či podprostoru malé dimenze. (I když typicky kvůli chybám měření to nevyjde přesně tak, ale s tím se umí lineární algebra vypořádat přes SVD.) Skvělá metafora jsou procesy se skrytou bází i mimo lineární algebru. To jsou procesy, které jsou na první pohled strašně složité, dokud se neobjeví vhodná skrytá báze, ve které je jejich popis strašně jednoduchý. Třeba pohyb planet je jednoduchý z pohledu univerzální gravitace.

Fibonacciho čísla je posloupnost definovaná následující rekurencí:

f₀ = 0, f₁ = 1  a  f_n+2 = f_n+1 + f_n.
Posloupnost je to zajímavá a splňuje řadu pěkných matematických vlastností. S pomocí volby vhodné báze nalezneme následující vzorec pro n-té Fibonacciho číslo:


Uvažme prostor všech fibonacciovských posloupností, což jsou posloupnosti splňující rekurenci s libovolnými hodnotami prvních dvou členů (a₀, a₁). Ty tvoří vektorový prostor dimenze dva. Pro ten chceme najít bázi tvořenou posloupnostmi, pro které bude jednoduchý vzorec pro n-tý člen: a_n = xⁿ pro nějaké reálné číslo x. Protože taková posloupnost musí splňovat rekurenci, platí xⁿ⁺² = xⁿ⁺¹ + xⁿ, neboli x² = x + 1. Řešením jsou dvě fibonacciovské posloupnosti tvořící bázi prostoru: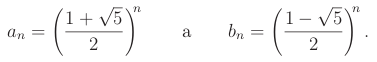

K získání vzorce zbývá dopočítat souřadnice vektoru (0,1): 𝛼 = 1/√5 a 𝛽 = -1/√5:

Geometrie vektorů

Vektorový prostor ℝⁿ je tvořen vektory, které geometricky odpovídají bodům. Vznikne obecněním ℝ² a ℝ³. Pro ně Deckard vymyslel, že sice prostor přímo nevidíme, ale můžeme v něm popisovat pozici pomocí trojice souřadnic (x,y,z).

Poznamenejme, že za vektory jsou někdy označovány orientované úsečky. Toto dělení bodů a vektorů je historické a dnes již zbytečné. Někdy s vektorem budeme pracovat jako s bodem, jindy se nám bude hodit interpretace, že je to šipka vycházející z počátku do tohoto bodu.

Násobení skalárem odpovídá natažení vektoru v daném směru. Pokud je koeficient záporný, bude výsledný vektor ukazovat opačným směrem.

Motivace pro sčítání dvou vektorů vychází z fyziky, konkrétně z Newtonovské mechaniky. Pokud vektory reprezentují působení síly (ta má velikost a směr), tak sčítání reprezentuje skládání těchto sil, tedy určení jedné zkombinované síly.

Vektorové podprostory

Vektorový podprostor W je neprázdná množina vektorů uzavřená na operace. To přesně znamená, že kdykoliv u a v patří do W, patří tam také u+v a c*u pro libovolné c. Speciálně počátek 0 vždy patří do W.

Studovat vektorové podprostory je užitečné ze dvou důvodů:

• Mají speciální strukturální vlastnosti, například sami o sobě tvoří vektorový prostor.
• Setkáváme se s nimi v lineární algebře na každém rohu.

Geometricky jsou vektorové podprostory ℝⁿ přímky, roviny a jejich vícerozměrná zobecnění procházející počátkem.

Uvažme všechny vektorové podprostory uspořádané inkluzí. Například pro ℝ³ získáme níže uvedený Hasseho diagram: Vidíme, že podprostory jsou rozděleny do vrstev podle dimenze.

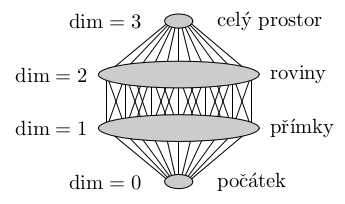
Tvrzení: Vektorové podprostory P tvoří úplný svaz, což znamená, že pro libovolnou podmnožinu vektorových prostorů S existuje infimum a supremum. Infimum je průnik všech podprostorů v S, kde průnik přes prázdnou podmnožinu je celý prostor. Supremum se definuje jako infimum všech podprostorů, které obsahují všechny podprostory v S, tedy jako jejich průnik.


Pokud vám definice suprema pomocí infima připadá podivná, rozmyslete si, že obecně stačí ukázat existenci pouze infim, nebo pouze suprem, existence toho druhého automaticky vyplývá.

Tagy: #klicove

Lineární kombinace

Výraz c₁*x₁ + ⋯ + c_n*x_n se nazývá lineární kombinace vektorů x₁,...,x_n.

Zároveň se výsledný vektor nazývá lineární kombinace.

Motivace pro studium lineárních kombinací je, že to jsou univerzální operace s vektory:

Tvrzení: Libovolná konečná posloupnost operací je ekvivalentní nějaké lineární kombinaci.

Důkaz: Indukcí podle stromu posloupnosti operací:

Tagy: #klicove

Řádková interpretace

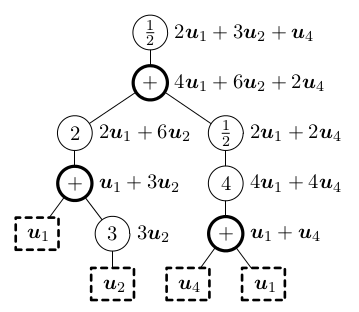
Mějme soustavu m rovnic o n neznámých. Jednotlivá ohodnocení neznámých můžeme identifikovat s vektory ℝⁿ. Jak vypadá množina všech řešení geometricky? Můžeme postupovat tak, že určíme množinu řešení R_i pro každý z řádků i=1,...,m. Celá množina řešení soustavy je průnik R₁ ∩ ⋯ ∩ R_m.

Příklady soustav 2 rovnic o 2 neznámých: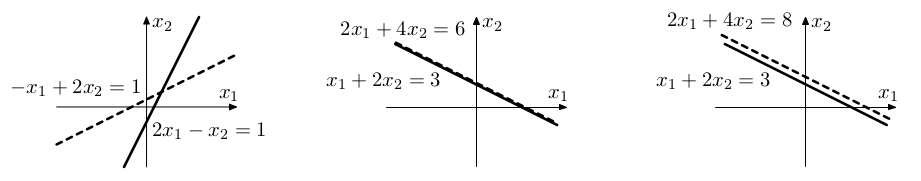 Vlevo je to jeden bod, ležící v průniku dvou přímek. Uprostřed je v průniku celá přímka. Vpravo je prázdný průnik, neboť jsou přímky rovnoběžné.

Jak vypadá množina R_i obecně?
Povšimněme si, že hodnoty libovolných n-1 proměnných můžeme zvolit libovolně, čímž je hodnota zbývající proměnné jednoznacně určena. Tedy R_i má n-1 "stupňů volnosti".

Geometricky R_i tvoří nadrovinu posunutou z počátku, což je afinní podprostor dimenze n-1, zobecnění rovin v ℝ³. Koeficienty a_i,1,...,a_i,n určují směr normálového vektoru, který je kolmý k nadrovině. Koeficient b_i určuje posunutí nadroviny z počátku.

Abychom toto mohli dokázat, museli bychom mít jinou geometrickou definici nadroviny. Zkuste si však rozmyslet, že to tak funguje pro malé hodnoty n. Konkrétně pro n=2 (vlevo) dostaneme přímku posunutou z počátku, pro n=3 (vpravo) získáme rovinu posunutou z počátku.


Tagy: #klicove

Vektorové prostory

Jeden z pohledů na lineární algebru je ten, že je to studium vektorových prostorů a jejich transformací (lineární zobrazení). Vektorové prostory jsou proto jedny z nejzákladnějších struktur v matematice. Jsou tvořené body, které se nazývají vektory, a tyto vektory umíme aplikovat dvě operace: sčítání a násobení skalárem.

Jsou dva možné přístupy, jak lze vektorový prostor definovat. (A ty obecně odpovídají dvěma rozdílným přístupům, jak lze v matematice popisovat objekty.) První je konstrukcí, kdy přesně specifikujeme, co jsou vektory a jak se na ně aplikují operace. Druhý abstraktní postup je přes popis vlastností. Řekneme, že vektorový prostor je tvořen nějakou množinou vektorů spolu s operacemi, které splňují daný seznam vlastností.

Jsou dva možné způsoby, jak lze definovat vektorový prostor.

Konkrétní konstrukce: Vektorový prostor ℝⁿ je tvořen n-ticemi x = (x₁,...,x_n), zvanými vektory, spolu s operacemi sčítání a násobení skalárem definovaných po složkách:

• x+y = (x₁+y₁,...,x_n+yn).
• c*x = (c*x₁,...,c*x_n).

Abstraktní definice: Vektorový prostor je tvořen nějakou množinou prvků, kterým se říká vektory, spolu s operacemi sčítání + a násobení skalárem *, které splňují následující vlastnosti:

• Komutativita +: u+v = v+u.
• Asociativita +: u+(v+w) = (u+v)+w.
• Neutrální prvek +: Existuje vektor 0 takový, že u+0=u pro každý vektor u.
• Inverzní prvky +: Pro každý vektor u existuje vektor (-u) takový, že u+(-u) = 0.
• Asociativita *: (a*b)*u = a*(b*u).
• Neutrální prvek *: 1*u = u.
• První distributivita: (a+b)*u = (a*u) + (b*u).
• Druhá distributivita: a*(u+v) = (a*u) + (a*v).

Tagy: #klicove

Lagrangeova interpolace

K vyřešení interpolace chceme najít vektor koeficientů a na prostoru polynomů ℙ_n stupně nejvýše n. Najít jeho souřadnice vůči kanonické bázi je obtížné a vede to řešení soustavy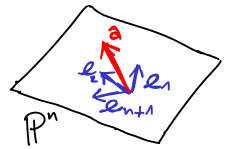

V_n+1a = y.
Lagrangeova interpolace je založena na myšlence, že problém se stane velice jednoduchý při volbě vhodné báze ℓ₁, ..., ℓ_n+1.

Bázi ℓ₁, ..., ℓ_n+1 zvolíme, aby každý z vektorů ℓ_i interpoloval jeden z bodů (x_i, y_i). Jejich jednoduchou lineární kombinací získáme hledaný vektor a. Podle Steinitzovy věty víme, že ℓ₁, ..., ℓ_n+1 je báze. Její existence dokazuje větu o jednoznačnosti polynomu P(x) stupně n procházejícího body (x₁,y₁), ..., (x_n+1,y_n+1).

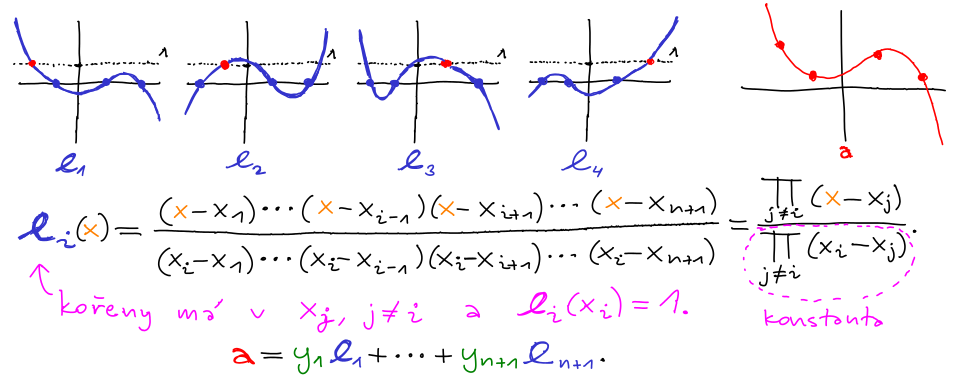
Samozřejmě je možné volit i jiné báze. Jedním příkladem je Newtonova interpolace, vůči bázi n₁, ..., n_n+1. Ta funguje skvěle na přidávání dalších bodů, neboť vektor n_i závisí pouze na bodech (x₁,y₁), ..., (x_i,y_i).

Geometrické příklady ℝ² → ℝ²

Řada geometrických zobrazení f : ℝ² ⟶ ℝ² splňuje linearitu:

• natažení,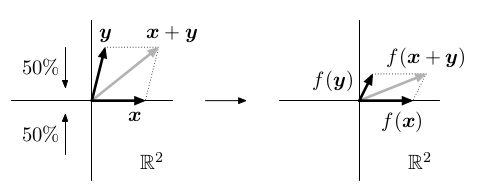
• rotace,
• zkosení,
• projekce a
• jejich kombinace.

Příklad nelineárního geometrického zobrazení f : ℝ² ⟶ ℝ² je posunutí ℝ² o libovolný nenulový vektor x.

Natažení: Rotace: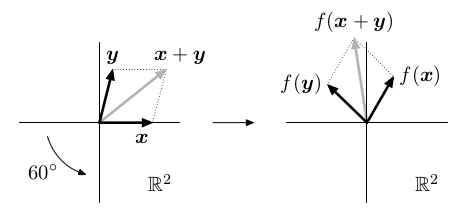

Zkosení: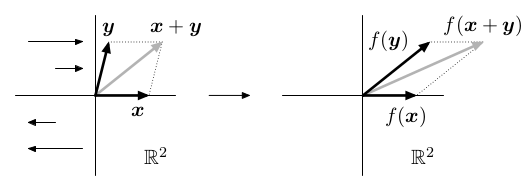 Kolmá projekce: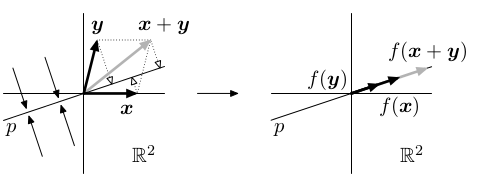

Geometrie elementárních úprav

Řádkové úpravy z pohledu sloupcové interpretace:
Řádkové úpravy transformují prostor ℝ^m spolu s vektory u₁,...,u_n a pravou stranou b. Klíčová vlastnost je, že pokud úprava prostor nikde nesplácne (tedy je regulární), je vztah mezi u₁,...,u_n a pravou stranou b zachován.

Elementární řádkové úpravy odpovídají následujícím geometrickým transformacím prostoru ℝ^m:

• Násobení i-tého řádku skalárem 𝛼 odpovídá 𝛼-násobnému natažení prostoru ve směru i-té souřadné osy.
• Přičtení i-tého řádku k j-tému odpovídá zkosení i-té souřadné osy do j-té souřadné osy.

V maticovém zápisu, nechť R je regulární matice řádkových úprav reprezentující geometrickou transformaci. Ze soustavy lineárních rovnic Ax=b získáme transformovanou soustavu RAx=Rb.

Sloupcové úpravy z pohledu sloupcové interpretace:
Sloupcová úprava transformuje jednotlivé sloupcové vektory u₁,...,u_n. Jejich vztah k pravé straně b se může změnit, tedy mění se množina všech řešení. Je možné provádět sloupcové úpravy, ale musíme si je zapamatovat a na závěr příslušně upravit nalezené řešení.

Elementární sloupcové úpravy odpovídají následujícím transformacím:

• Násobení i-tého sloupce skalárem 𝛼 odpovídá 𝛼-násobnému natažení vektoru u_i.
• Přičtení i-tého sloupce k j-tému odpovídá zkosení u_i do u_j.

V maticovém zápisu, nechť S je regulární matice sloupcové úpravy reprezentující transformaci sloupcových vektorů. Ze soustavy lineárních rovnic Ax=b získáme transformovanou soustavu ASS^-1x=b, která vede na soustavu ASy=b. Když ji vyřešíme a nalezneme hodnotu y, musíme dopočítat x=Sy.

Geometrická struktura množiny všech řešení

Věta: Množina všech řešení soustavy Ax=0 je vektorový podprostor, který se značí Ker(A).

Důkaz: Stačí ukázat, že množina všech řešení je uzavřená na sčítání a násobení skalárem. Když x je řešením soustavy Ax=0, platí pro i-tou rovnici:

Množina řešení je uzavřená na sčítání, neboť se zachovává se splnění i-té rovnice:

Důkaz uzavřenosti na násobení je podobný.

V maticovém zápisu je to ještě jednodušší. Pokud Ax=0 a Ay=0, potom

A(c*x) = c*(Ax)=c*0=0 a A(x+y) = Ax+Ay = 0+0 = 0.

Věta: Množina všech řešení soustavy Ax=b je afinní podprostor Ker(A)+p, kde p je libovolné řešení soustavy.

Důkaz: Stačí si všimnout, že kdykoliv máme dvě řešení Ax=b a Ay=b, jejich rozdíl x-y patří do Ker(A):
A(x-y) = Ax-Ay = b-b = 0.
Zbytek plyne z vlastností afinních podprostorů.

Klíčový důsledek: Uvažme různé pravé strany b. Pro některé nebude existovat žádné řešení, což odpovídá neexistence vektoru p. Pro ty zbývající jsou to afinní podprostor vzniklé různými posunutími Ker(A). Tedy množiny řešení soustav Ax=b a Ax=c mají totožnou strukturu až na posunutí.

Označíme Im(A) množinu všech pravých stran, pro kterou existuje řešení, to je vektorový podprostor ℝ^m (neboť afinní podprostory vzniklé posunutím W tvoří vektorový prostor). Platí, že čím větší je Ker(A), tím méně jeho posunutí existuje, tedy tím méně pravých stran má řešení. Tento vztah lze přesně popsat pomocí dimenzí:
dim Ker(A) + dim Im(A) = n.

Tagy: #klicove

Sloupcová interpretace

I když se tato interpretace často ignoruje, považuji ji za mnohem užitečnější než tu řádkovou. Myšlenka je, že budeme uvažovat sloupcové vektory matice a pravé strany, které patří do ℝ^m: Nyní učiníme klíčové pozorování, že se neznámá x_i objevuje přesně u koeficientů jednoho sloupcového vektoru u_i. Tedy soustava lineárních rovnic je ekvivalentní s vektorovou rovnicí kde rovnost má platit v každé složce.

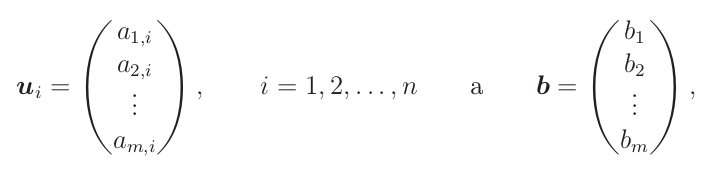
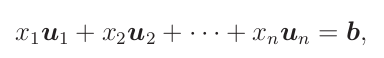
Tedy máme rovnici kterou chceme interpretovat geometricky. Hledáme koeficienty x₁,...,x_n natažení vektorů u₁,...u_n, tak aby se zkombinovali pravou stranu b. Voleb koeficientů může být spousta, což vede k nekonečně mnoha řešením. Pokud vektory u₁,...u_n ukazují "jiným" směrem než b, soustava nemá žádné řešení.

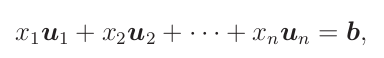
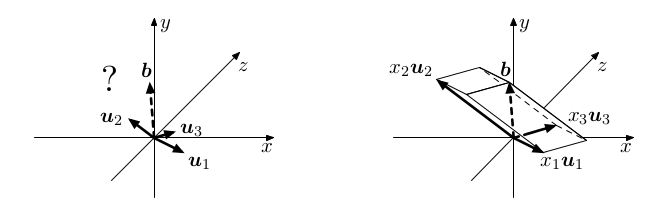
Tagy: #klicove

Interpolace polynomů

Soustavami lineárních rovnic lze rešit problém, který s nimi na první pohled vůbec nesouvisí. Uvažme polynomy

P(x) = a_n*xⁿ + a_n-1*x^n-1 + ⋯ + a₁*x + a₀.
stupně n. Platí následující algebraická věta, úzce související s fundamentální větou algebry.

Věta: Existuje právě jeden polynom P(x) stupně n, který prochází libovolnými n+1 body

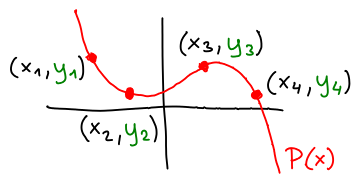
(x₁,y₁), ..., (x_n+1,y_n+1),
kde x_i ≠ x_j pro i ≠ j, tedy P(x_i) = y_i.

Hledání koeficientů tohoto polynomu se nazývá interpolace polynomů a je možné to udělat vyřešením soustavy lineárních rovnic.

K nalezení koeficientů stačí vyřešit následující soustavu, kde y = (y₁, ..., y_n+1) a vektor a je vektor hledaných koeficientů polynomu P(x).


Větu o jednoznačnosti interpolace je možné dokázat pomocí lineární algebry. Stačí dokázat, že Vandermondova matice V_n+1 je regulární, právě když x_i ≠ x_j pro i ≠ j. Jiný důkaz vyplývá z Lagrangeovy interpolace.

Maticová reprezentace f : x ↦ A x

Věta: Libovolné lineární zobrazení f : U ⟶ V je reprezentováno maticí tak, že f : x ↦ Ax, tedy f(x) = Ax.

Důkaz: Zobrazení x ↦ Ax je vždy lineární zobrazení z distributivity maticového násobení: A(x+y) = Ax + Ay a A(c*x) = c*(Ax).

Na druhou stranu, zobrazení f : ℝⁿ ⟶ ℝ^m je z linearity jednoznačně popsané obrazy f(e₁), ..., f(e_n):

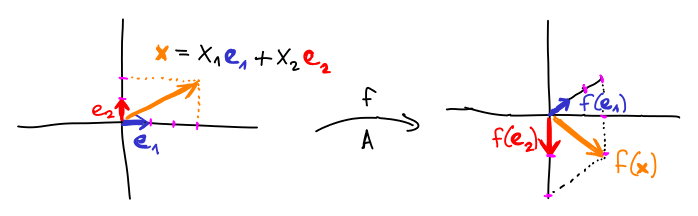
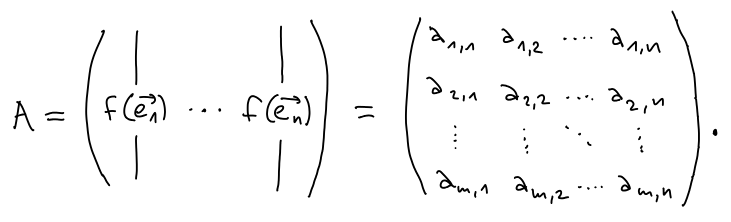
Pro x = (x₁, ..., x_n) = x₁*e₁ + ⋯ + x_n*e_n je f(x) = x₁*f(e₁) + ⋯ + x_n*f(e_n). Každý z obrazů f(e_i) má m souřadnic, dohromady je tedy f jednoznačně určené pomocí m x n souřadnic, které zapíšeme po sloupcích do tabulky A zvané matice.
Z definice maticového násobení je Ax = x₁*f(e₁) + ⋯ + x_n*f(e_n), tedy f(x) = Ax.

Víme, že lineární zobrazení f : U ⟶ V je jednoznačně určeno obrazy libovolné báze. Zvolíme libovolně dvě báze:

• X = {x₁,...,x_n} jako bázi prostoru U,
• Y = {y₁,...,y_m} jako bázi prostoru V.

K popisu zobrazení stačí znát f(x₁),...,f(x_n), kde každý z těchto obrazů lze popsat pomocí m souřadnic vůči bázi Y.

Rozhodneme se zapsat těchto m x n souřadnic do tabulky A, které budeme říkat matice. Souřadnice jednotlivých vektorů f(x_i) zapíšeme do sloupců:

Tedy a_i,j je souřadnice f(x_j) vůči y_i.

Věta: Nechť A je maticová reprezentace f a nechť x je vyjádřený vůči bázi X. Potom jsou souřadnice f(x) vůči bázi Y ve vektoru Ax. Tedy f : x ↦ Ax.

Klíčové: Pro různé volby bází X a Y můžeme získat různé maticové reprezentace lineárního zobrazení f. Naopak jedna matice může reprezentovat různá lineární zobrazení pro různou volbu bází.

Například uvažme rotaci o úhel 𝜑 v rovině. Ta je reprezentovaná maticí A, pokud X=Y je kanonická báze tvořená vektory (1,0) a (0,1). Pokud však X je kanonická báze a Y je X otočená o úhel 𝜑, je rotace reprezentovaná maticí B. Na druhou stranu, pokud X=Y a zobrazení je endomorfismus, reprezentuje matice B identické zobrazení.

Tagy: #klicove

Derivace a integrál

Geometrie Gaussovy eliminace

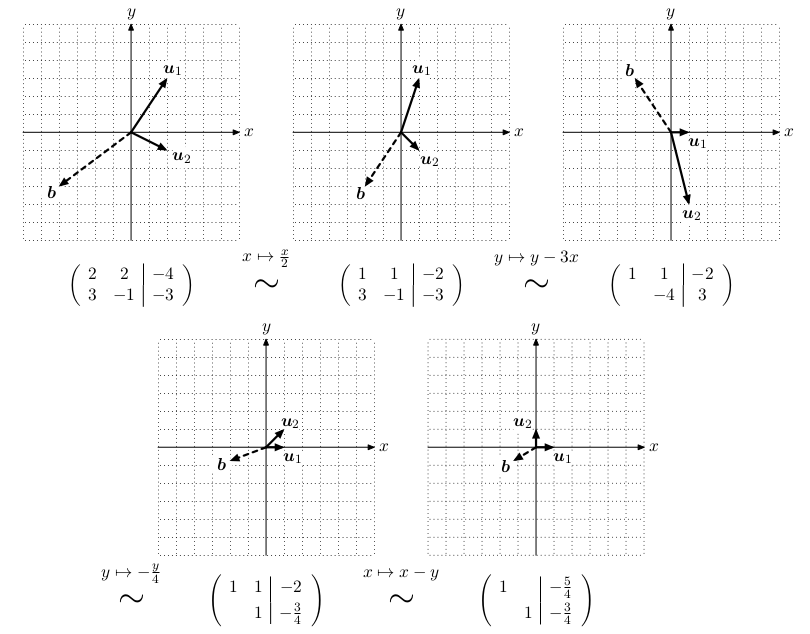
Gaussova eliminace provádí geometrické transformace sloupcových vektorů a pravé strany elementárními řádkovými úpravami. Převede soustavu do odstupňovaného tvaru se sloupcovými vektory u₁,...,u_n a pravou stranou b, ve kterém je snadné ji vyřešit.

Pokud b ukazuje jiným směrem než sloupcové vektory, poznáme to podle toho, že ukazuje ve směru souřadné osy, která není obsažena v žádném ze sloupcových vektorů u₁,...,u_n. Tedy b nelze vyjádřit pomocí sloupcových vektorů u₁,...,u_n a řešení soustavy neexistuje.

Pokud jsou všechny tyto koeficienty b nulové, řešení existuje. Najdeme ho tak, že hodnoty volných proměnných zvolíme libovolně, čímž známe natažení příslušných sloupcových vektorů. Můžeme je odečíst od pravé strany a získat upravenou pravou stranu b'. Pro sloupcové vektory s pivoty dopočteme hodnotu řešení, protože vždy pouze jeden z nich ukazuje určitým směrem b', tedy jeho hodnota natažení je jednoznačně určena a lze příslušný sloupcový vektor odečíst.

Věta o homomorfismu

Věta: Pro libovolné lineární zobrazení f : U ⟶ V platí, že
U / Ker(f) ≅ Im(f).
Víme, že vzorem jednotlivých vektorů z Im(f) jsou afinní podprostory U vzniklé posunutím Ker(f). Tedy vzory jednotlivých vektorů z Im(f) mají stejnou strukturu až na posunutí.

Platí, že čím větší je Ker(f), tím méně jeho posunutí existuje, tedy tím méně vzorů má řešení. Přesněji, ve řeči dimenzí:

dim Ker(f) + dim Im(f) = dim(U).

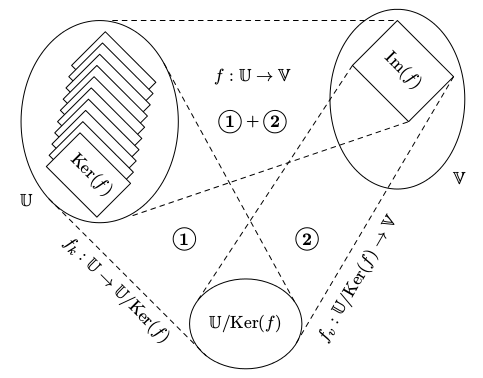
Podle věty lze homomorfismus f : U ⟶ V rozdělit na složení dvou jednodušších homomorfismů:

• Kvocientový homomorfismus
  f_k : U ⟶ U / Ker(f), který je na a obecně není prostý.
• Vnořovací homomorfismu
  f_v : U / Ker(f) ⟶ V, který je prostý, ale obecně není na.

Maticový zápis

Můžeme zjednodušit zápis soustavy tak, že vynecháme zbytečné informace:

• V jednotlivých sloupcích jsou stejná jména proměnných, která vynecháme.
• Odstraníme operace + a =.

Pro řešení soustavy jsou důležité pouze koeficienty, které zapíšeme do tabulky zvané matice.

Původní soustava: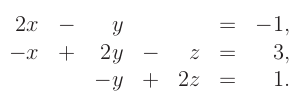

Maticový zápis: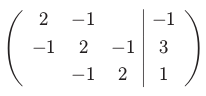

Soustavu lze v řeči matic a vektorů vyjádřit v elegatní formě Ax=b. Zde A je matice koeficentů, x je vektor neznámých a b je vektor pravých stran.


Rozepsáním definice maticového násobení získáme soustavu lineárních rovnic.

Interpretace maticového násobení po sloupcích A vede na sloupcovou interpretaci soustavy.

Tagy: #klicove

Věta o izomorfismu

Věta: Libovolný vektorový prostor V dimenze n je izomorfní vektorovému prostoru ℝⁿ.

Slovo izomorfní znamená, že existuje izomorfismus f : V ⟶ ℝⁿ. Ten zaručuje, že algebraická struktura prostorů V a ℝⁿ je totožná, tedy struktura jejich operací. Platí f(x+y) = f(x)+f(y), podobně pro násobení, tedy jednotlivé vektory x prostoru V lze identifikovat s vektory f(x) prostoru ℝⁿ.

Neznamená to, že by tyto prostory byly totožné, například V může být prostor polynomů stupně nejvýše n-1, a tedy jeho prvky jsou úplně jiné matematické objekty než n-tice reálných čísel. Avšak izomorfismus říká, že v řadě situací můžeme pracovat s V přesně jako s ℝⁿ, například lze řešit soustavy nad ℝⁿ místo nad abstraktním prostorem V.

Důkaz: Zvolíme libovolnou bázi prostoru V. Ta definuje souřadnice (c₁,...c_n) nad V. Tato definice souřadnic je hledaný izomorfismus:

f : c₁*b₁ + ... + c_n*b_n ⟼ (c₁,...,c_n).
Protože souřadnice jsou definované pro každý vektor V jednoznačně, je definované zobrazení bijekce. Zbývá ověřit, že to skutečně je lineární zobrazení. Stačí si všimnout, že sčítání vektorů ve V odpovídá sčítání jejich souřadnic, podobně pro skalární násobení.
Tagy: #klicove

Analýza dynamických systémů

Velká část matematiky se zabývá studiem modelů reálného světa. To jsou často dynamické systémy, jejichž stav (například vektor reálných čísel) se mění v závislosti na čase. Změna stavu je popsána matematickými vztahy, například lokálně diferenciálními rovnicemi. Při analýze chceme odpovídat na otázky následujícího typu: predikce vývoje z počátečního stavu, pochopit kvalitativní chování (konvergence k ustálenému stavu, oscilace, chaotické chování).

Problém je, že typický dynamický systém je příliš složitý a nemůže být přesně popsán jeho vývoj. Ve většině situací se spokojíme s tím, že nalezneme přibližné řešení jeho diskretizací (simulace, metoda konečné mřížky, metoda konečných prvků), čímž se v řadě situací převede na řešení velké soustavy lineárních rovnic

Ax=b.
Zde matice A popisuje zdiskretizované vztahy v systému, zatímco vektor b odpovídá stavu nebo vývoji stavu. Při řešení se často využívá specifické struktury koeficientů matice A.

Historie

Řešení soustav lineárních rovnic je odvěký problém se spoustou aplikací. Konkrétní soustavy lineárních rovnic se v matematice objevují již před více než pěti tisíci lety. V čínské knize Devět kapitol napsané zhruba dvě stě let před naším letopočtem se objevuje postup, jak vyřešit konkrétní soustavu tří lineárních rovnic o třech neznámých. Jakékoliv formální zdůvodnění chybí, ale při zobecnění dostaneme Gaussovu eliminaci.

V západní matematice Gaussovu eliminaci poprvé popsal Newton ve své algebraické knize, i když se jednalo o postup mezi matematiky běžně známý.

Gauss se zabýval metodou nejmenších čtverců (v souvislosti s geodézií), pro níž popsal algoritmus podobný Gaussově eliminaci. Jméno Gaussova eliminace se začalo používat až v padesátých letech díky implementaci metody nejmenších čtverců v počítačích. Historie řady pojmů lineární algebry je značně složitá!

Regulární matice

Čtvercová matice se nazývá regulární, pokud je invertovatelná. Ostatní čtvercové matice se nazývají singulární. O inverzích regulárních matic platí následující věta:

Věta: Pro čtvercovou matici existuje levá inverze, právě když existuje pravá inverze. Navíc jsou stejné a určené jednoznačně.

Těžká je první část, která je speciální případ rovnosti rank(A) = rank(A^T). Druhá část snadno vyplývá z asociativity. Pokud X je levá inverze a Y je pravá inverze, platí:

X = XI_m = X(AY) = (XA)Y = I_nY = Y.

Tagy: #klicove

Hledání vzorů

Nechť f : U ⟶ V je lineární zobrazení a b je libovolný vektor V. Chceme nalézt množinu vzorů
f^-1(b) = {x : f(x) = b}.

Nechť lineární zobrazení f je reprezentováno maticí A. Víme, že f : x ↦ Ax. Tedy hledáme všechny vektory x, které splňují Ax = b, což vede na soustavu lineárních rovnic. Tedy i kdybychom lineární algebru budovali abstraktně, od vektorových prostorů a jejich homomorfismů, je řešení soustav lineárních rovnic klíčové.

Víme, že množina vzorů f^-1(b) je neprázdná, právě když b ∊ Im(f). V takovém případě je to afinní podprostor Ker(f)+p, kde p je libovolný vzor b.

Tagy: #klicove

Lineární zobrazení (homomorfismy)

Nechť U a V jsou dva vektorové prostory. Zobrazení f : U ⟶ V je lineární, pokud splňuje:
Lineární zobrazení f vnořuje strukturu U do struktury V. Například pokud platí libovolná rovnost x + y = z, platí i pro jejich obrazy: f(x) + f(y) = f(z). Poznamenejme, že obrazy rovností mohou být velice triviální.

Lineární zobrazení se nazývají homomorfismy. Homomorfismy se uvažují nad obecnými matematickými strukturami a jejich zkoumání je velice důležité. Název se skláda z homo (zachovávání struktury) a morfismus (transformace jedné struktury v druhou).

Učiňme nejprve pozorování, že pro libovolné lineární zobrazení f platí, že f(0) = 0. Obrazem počátku musí být počátek z linearity:

f(0) = f(0*0) = 0*f(0) = 0.
Podobně platí následující:

Tvrzení: Obrazem libovolné lineární kombinace je lineární kombinace obrazů. Proto je lineární zobrazení jednoznačně určené obrazy libovolné báze.

Důkaz: Využijeme linearitu: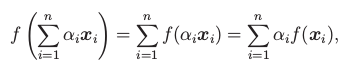
Tagy: #klicove

Skládání zobrazení

Mějme lineární zobrazení f : U ⟶ V a g : V ⟶ W. Existuje složené zobrazení g ∘ f : U ⟶ W, které je také lineární. Jak vypadá jeho maticová reprezentace?

Věta: Nechť
A reprezentuje f : U ⟶ V vůči bázím X a Y,B reprezentuje g : V ⟶ W vůči bázím Y a Z. Potom
BA reprezentuje g ∘ f : U ⟶ W vůči bázím X a Z.

Tato věta vysvětluje definici maticového násobení. Matice musíme násobit tak zvláštně právě proto, aby jejich násobení odpovídalo skládání lineárních zobrazení. Pokud bychom lineární algebru budovali od lineárních zobrazení, můžeme z definice maticové reprezentace odvodit definici maticového násobení.

Proto také definice maticového násobení vyžaduje kompatibilní rozměry. Nechť A je velikosti n x p, reprezentující zobrazení ℝ^p ⟶ ℝⁿ, a B je velikosti m x n, reprezentující zobrazení ℝⁿ ⟶ ℝ^m. Potom je prostor uprostřed totožný, tedy má i stejnou dimenzi, a složené zobrazení ℝ^p ⟶ ℝ^m je reprezentováno maticí BA velikosti m x p.

Důkaz z definice: Matice reprezentující g ∘ f vůči bázím X a Z musí mít v i-tém sloupci souřadnice g(f(x_i)) vůči bázi Z. Povšimneme si, že v i-tém sloupci matice A máme souřadnice f(x_i) vůči bázi Y, a obrazy jednotlivých vektorů báze Y jsou ve sloupcích B. Tedy souřadnice g(f(x_i)) vůči bázi Z získáme jako zkombinování sloupců B podle souřadnic v i-tém sloupci A, což přesně odpovídá maticovému násobení.

Důkaz z asociativity: Z asociativity maticového násobení víme, že (BA)x = B(Ax) pro libovolný vektor x. Pravá strana odpovída složenému zobrazení g ∘ f : x ↦ B(Ax). Protože rovnost platí pro libovolný vektor x, musí být g ∘ f reprezentováno BA.

Poznamenejme, že naopak z této věty vyplývá asociativita maticového násobení. To totiž odpovídá skládání lineárních zobrazení, a skládání libovolných zobrazení je asociativní.

Tagy: #klicove

Matice přechodu

Čtvercová regulární matice reprezentující identitu se nazývá matice přechodu. Přepočítává souřadnice od jedné báze X k jiné bázi X'.

Čtvercová regulární matice může reprezentovat různá lineární zobrazení. Pokud zvolíme jednu bázi X, dostáváme nějaký endomorfismus. Lze ji však uvažovat jako reprezentace identity vůči volbě bází X a X'.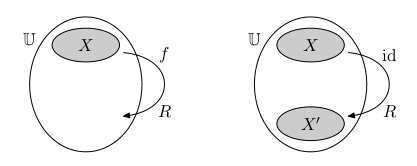

Pokud x jsou souřadnice vektoru vůči bázi X, jsou Ax souřadnice stejného vektoru vůči bázi X'.

Příklady eliminací

Dopředná eliminace:

Zpětná substituce:

• Nejprve určíme z=2.
• Poté dosadíme za z do druhé rovnice a určíme y=3.
• Nakonec dosadíme za y a z do první rovnice a získáme x=1.

Tedy existuje jednoznačné řešení soustavy (1,3,2).

Soustava vlevo:
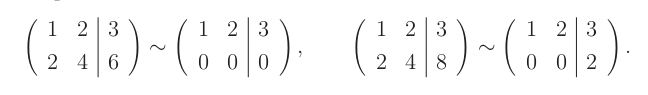
Má nekonečně mnoho řešení ve tvaru (3-2y,y), kde y je libovolné reálné číslo. Lze popsat také jako (3,0) + y*(-2,1).

Soustava vpravo:
Neexistuje žádné řešení, neboť jsme úpravami odvodili, že musí platit 0x+0y=2, což není splněno pro žádnou dvojici (x,y) reálných čísel.

Gaussova eliminace

Algoritmus na řešení soustavy lineárních rovnic. Jedná se o strategii, jak aplikovat elementární úpravy tak, aby se matice zjednodušila do odstupňovaného tvaru.

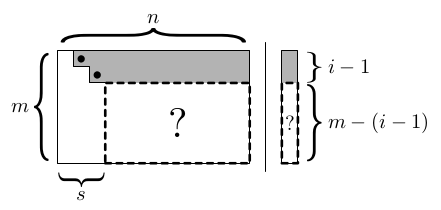
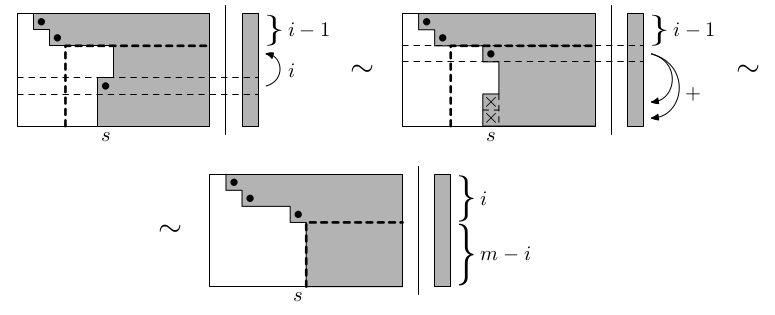
Černě vyznačené koeficienty se nazývají pivoti a jsou to první nenulové hodnoty na jednotlivých řádcích. Gaussova eliminace se skládá ze dvou fází:

• dopředná eliminace, která vypočítá odstupňovaný tvar,
• zpětná substituce, která nalezne všechna řešení z odstupňovaného tvaru.

Odstupňovaný tvar je konstruován v n krocích, celkově k jeho spočítání potřebujeme n³/3 elementárních operací (násobení, sčítání).

Stav na počátku i-tého kroku:
V i-tém kroku se aplikují následující elementární úpravy:

Tagy: #klicove

Matice

Matice je tabulka m x n reálných čísel:

Matice velikosti m x n popisuje geometrickou transformaci vektorového prostoru ℝⁿ do vektorového prostoru ℝ^m.

Pro matici A označme (A)_i,j = a_i,j koeficient v i-tém řádku a j-tém sloupci. Řádky matice tvoří řádkové vektory ℝⁿ, sloupce tvoří sloupcové vektory ℝ^m.

Základní maticové operace jsou násobení skalárem a sčítání: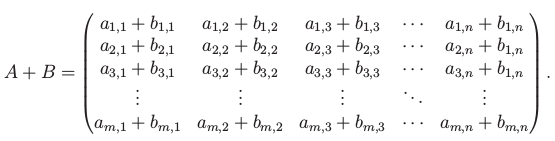
Všechny matice velikosti m x n proto tvoří vektorový prostor ℝ^{m x n}.

Tagy: #klicove

Podobnost

Dvě matice A a B jsou ekvivalentní, pokud reprezentují stejné lineární zobrazení pro různou volbu bází. Jsou ekvivalentní, právě když existují dvě regulární matice R a S (přechodu), pro které platí:

A = SBR, neboli B = S^-1AR^-1.

Podobnost je maticová ekvivalence pro čtvercové matice reprezentující endomorfismy vůči jedné bázi. Tedy dvě matice A a B jsou podobné, právě když reprezentují stejný endomorfismus pro jinou volbu báze. To je právě tehdy, když existuje regulární matice R (matice přechodu), že platí:
A = R^-1BR, neboli B=RAR^-1.

Matice úprav

Regulární úpravy odpovídají regulárním maticím. Soustava Ax=b se upraví na soustavu RAx=Rb, kde R je nějaká regulární matice.

Tvrzení: Pokud R je regulární matice, je množina řešení Ax=b a RAx=Rb je stejná.

Důkaz: Pokud x řeší původní soustavu, určitě také řeší upravenou soustavu. Tedy množina řešení se může každou úpravou pouze zvětšit. Protože je R regulární, existuje inverzní úprava R^-1, která převede upravenou soustavu zpět do původního stavu:
R^-1RAx = R^-1Rb ⟹ Ax = b. Proto musí být množina řešení stejná, jinak by se úpravou R^-1 zmenšila, což není možné.

Regulární matice R elementárních řádkových úprav jsou velice jednoduché. Vlevo je přičtení i-tého řádku k j-tému. Vpravo je vynásobení i-tého řádku koeficientem 𝛼 ≠ 0. Čtenář si může rozmyslet, jak vypadají matice odvozených elementárních úprav: přičtení 𝛼-násobku i-tého řádku k j-tému a prohození dvou řádků.

Maticové násobení

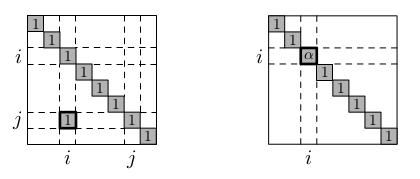
Nechť A∊ℝ^{m x n} a B∊ℝ^{n x p}. Potom je součin AB matice velikosti m x p s následujícími koeficienty:

Příklad maticového součinu: (vlevo A, nahoře B)

Toto je pohled řádek-sloupec na maticové násobení. Existují však ještě tři další užitečné pohledy:

• Pohled sloupec-sloupec: Nejprve se zaměřme na součin Ax. (Zde s vektorem pracujeme jako s maticí, co má jeden sloupec.) Podle definice jsou jednotlivé sloupcové vektory u₁,...,u_n matice A násobeny jednotlivými koeficienty vektoru x a sečteny. Tedy dostáváme lineární kombinaci
  Ax = x₁*u₁ + ⋯ + x_n*u_n. Matice AB obsahuje jako sloupcové vektory lineární kombinace sloupcových vektorů A s koeficienty podle sloupcových vektorů B.
• Pohled řádek-řádek: Identický s předchozím, pouze transponovaně, získáváme lineární kombinace řádků B podle koeficientů matice A.
• Pohled sloupec-řádek: V definici součinu vždy koeficienty i-tého sloupce matice A násobí pouze koeficienty i-tého řádku matice B. S využitím distributivity lze tedy spárovat sloupce x₁,...,x_n matice A s řádky y₁^T,...,y_n^T matice B. Dostáváme následující součet n matic m x p:
  AB = x₁ y₁^T + ⋯ + x_ny_n^T.

Tagy: #klicove, #nasobeni_matic

Endomorfismy, izomorfismy, automorfismy

Používají se tři prefixy pro speciální druhy homorofismů: endomorfismy, izomorfismy a automorfismy. Ty rozlišují jestli je f zobrazení obecné nebo bijektivní, a jestli f zobrazuje mezi dvěma prostory U a V, nebo z prostoru U do téhož prostoru U.

	f : U ⟶ V	f : U ⟶ U
obecně	homomorfismus	endomorfismus
f je bijekce	izomorfismus	automorfismus

Každý endomorfismus je homomorfismus a každý automorfismus je izomorfismus, ale jména specificky zdůrazňují, že je uvažujeme jako zobrazení z jednoho prostoru do téhož prostoru. Složení endomorfismů jsou endomorfismy, navíc je lze mocnit:
f^k = f ∘ f ∘ ⋯ ∘ f.
Endomorfismy jsou reprezentované čtvercovými maticemi a typicky se volí pouze jedna báze, tedy X=Y. Výhody takových reprezentací jsou, že iterování homomorfismu odpovídá mocninám reprezentující matice:
Pokud f je reprezentováno A, je f^k reprezentováno A^k.
Izomorfismy jsou reprezentované regulárními maticemi. Pokud existuje izomorfismus f : U ⟶ V, mají prostory U a V stejnou algebraickou strukturu vektorových operací + a *. Protože f je bijekce, můžeme vektory U spárovat s vektory V, a operace se na nich aplikují identicky. Neznamená to, že by tyto prostory byly totožné matematické objekty, akorát jejich algebraická struktura je totožná a v řadě případů můžeme pracovat v U stejně jako ve V.

Tagy: #klicove

Iterační metody

Obecně existují v matematice dva druhy výpočetních metod. Přímé metody (například Gaussova eliminace) provádějí dlouhou sekvenci kroků, na jejichž koncí získáme řešení. Oproti tomu iterační metody postupují v kratších krocích a konstruují lepší a lepší aproximaci řešení.

V případě soustavy Ax=b počítají iterační metody posloupnost přibližných řešení x₀,...,x_k. Skončíme v k-tém kroku, když je chyba e_k=x-x_k dostatečně malá. Protože typicky vektor chyby e_k neznáme, testujeme dostatečně malou velikost residua

r_k = Ae_k = A(x-x_k) = b - Ax_k.
Jeden ze zásadních rozdílů je, že pokud iterační metodu zastavíme v půlce, získáme alespoň nějaký odhad řešení, narozdíl od přímé metody. (Co víme o řešení soustavy, pokud Gaussova eliminace spočítá pouze polovinu odstupňovaného tvaru?)

Štěpící metody. Předpokládejme, že A = S - T a že pro matici S umíme snadno vyřešit soustavu (řekněme, že známe S^-1). Potom Ax=b vede na Sx=Tx+b, neboli x=S^-1Tx+S^-1b. Tento vzorec můžeme použít k iterování:
x_k+1 = S^-1Tx_k+S^-1b.
Metoda konverguje pouze pro určité volby matic S a T, a velice pomalu. Typická volba S je diagonální část A nebo horní trojúhelníková část A. Jiný pohled na metody je, že S je aproximace matice A.

Metoda konjugovaných gradientů CG. Konstruuje postupně aproximace výpočtem Krylovova podprostoru

K_k = ⟨b, Ab, A²b, ..., A^k-1b⟩.
Volíme x_k∊K_k tak, aby minimalizovalo chybu řešení přes všechny vektory K_k, což lze udělat velice efektivně. Pro rozšíření Krylovova podprostoru je potřeba vynásobit vektor maticí, což vyžaduje n² operací. Protože typicky stačí udělat n^1/2 iterací, je metoda typicky rychlejší než Gaussova eliminace: n^5/2 operací.

Hodnost transpozice

Následující věta je jedním z divů lineární algebry. Říká, že pro libovolnou matici A je dim Im(A) = dim R(A), přestože se jedná o zcela jiné prostory.

Věta: Pro libovolnou matici A platí, že rank(A) = rank(A^T).

Maticové inverze

Mějme matici A velikosti m x n. Pokud existuje matice A^-1 velikosti n x m splňující AA^-1 = I_m, nazývá se A^-1 pravá inverze A. Nemusí být určena jednoznačně. Podobně se definuje levá inverze A^-1, která splňuje A^-1A = I_n.

Označme u₁,...,u_m sloupce pravé inverze A^-1. Musí splňovat soustavy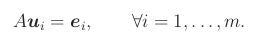
Lze nalézt jednou Gaussovou eliminací s více pravými stranami:

Uveďme několik tvrzení o existence inverzí, čtenář si může rozmyslet jejich důkazy:

Tvrzení: Pro matici A existuje pravá inverze, právě když má soustava Ax=b řešení pro každou pravou stranu b. Neboli Im(A) je celý prostor ℝ^m.

Tvrzení: Nechť A je matice velikosti m x n. Pokud existuje pravá inverze, je m≤n. Pokud existuje levá inverze, je m≥n. Tedy oboustranná inverze může existovat pouze pro čtvercové matice.

Tvrzení: Pro matici A existuje pravá inverze, právě když existuje levá inverze pro matici A^T.

Tvrzení: Matice A velikosti m x n má pravou inverzi, právě když rank(A)=m, a levou, právě když rank(A)=n. (To vychází z netriviálního faktu, že rank(A) = rank(A^T).)

Úprava inverzní maticí: Pokud má matice A levou inverzi, můžeme provést úpravu Ax=b na A^-1Ax=A^-1b, neboli x=A^-1b. Nepoužívá se při výpočtech, protože spočítat inverzní matici je složitější než vyřešit soustavu; avšak hodí se v teorii.

Tagy: #klicove

Inverzní zobrazení

Pro lineární zobrazení f : U ⟶ V může existovat inverzní zobrazení f^-1 : V ⟶ U, nebo nemusí. Rozlišujeme tyto druhy inverzí:

• Levá inverze f^-1 ∘ f = id existuje, právě když je zobrazení f prosté.
• Pravá inverze f ∘ f^-1 = id existuje, právě když je zobrazení f na.
• Oboustranná inverze f^-1 ∘ f = f ∘ f^-1 = id existuje, právě když je zobrazení f bijektivní.

Protože identita je reprezentováná jednotkovou maticí I_n, je inverzní zobrazení reprezentováno inverzní maticí. Přesněji řečeno, nechť f je reprezentováno maticí A vůči bázím X a Y.

• Levá inverze f^-1 je reprezentována levou inverzí A^-1 vůči bázím Y a X (obrázek vlevo).
• Pravá inverze f^-1 je reprezentována pravou inverzí A^-1 vůči bázím Y a X (obrázek vpravo).
• Oboustranná inverze f^-1 je reprezentována oboustrannou inverzí A^-1 vůči bázím Y a X.

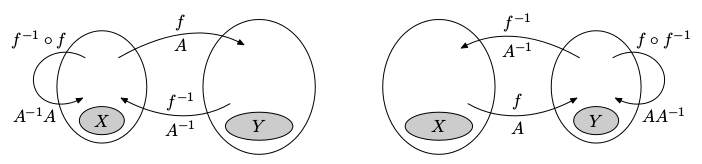Tagy: #klicove

Úpravy

Z rovnic lze vyvozovat nové informace jejich kombinováním. Budeme uvažovat dvě elementární operace a jejich kombinace:

• Násobení reálným číslem: z A=B získáme αA=αB.
• Součet dvou rovnic: z A=B a C=D získáme A+C=B+D.

Protože nechceme, aby počet rovnic rostl, vždy odvozenou rovnicí nahradíme nějakou předchozí, čímž získáme upravenou soustavu. Výše uvedené úpravy nazýváme elementární úpravy.

Dále uvažujeme odvozené elementární úpravy:

• Přičtení 𝛼-násobku jedné rovnice k druhé.
• Prohození dvou rovnic.

Pokud nějaká n-tice (x₁,...,x_n) řeší soustavu, bude řešit i upravenou soustavu. Avšak obrácená implikace nemusí platit, množina řešení se může úpravou zvětšit.

Úprava se nazývá regulární (nebo ekvivalentní), pokud nemění množinu řešení obecně libovolné soustavy.

Tvrzení: Úpravy vynásobení nenulovým reálným číslem, přičtení jedné rovnice k druhé a jejich kombinace jsou regulární.

Důkaz: Výše uvedené úpravy lze invertovat, tedy existují úpravy, které převedou upravenou soustavu zpět do původního tvaru. Protože se množina řešení může pouze zvětšovat, nemohla se změnit.



Tagy: #klicove

LU dekompozice

Věta: Pro libovolnou matici A velikosti m x n existuje dekompozice PA = LU, kde

• P je permutační matice m x m,
• L je dolní trojúhelníková matice m x m s jednotkovou diagonálou,
• U je horní trojúhelníková matice m x n.

Občas se uvažuje symetričtější varianta dekompozice PA=LDU, kde obě trojúhelníkové matice L a U mají jednotkové diagonály a D je diagonální matice pivotů.

Příklad: Nechť A je následující matice:
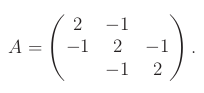Získáváme následující LU a LDU dekompozice pro P=I₃: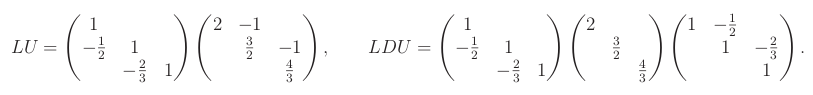

LU dekompozice je maticový zápis Gaussovy eliminace aplikované na A. Význam jednotlivých matic v dekompozici je následující:

• Permutační matice P popisuje proházení řádků A tak, aby bylo možné provést Gaussovu eliminace PA bez pivotace.
• Matice L popisuje elementární úpravy dopředné eliminace. Protože jsme proházeli řádky pomocí P, stačí využívat pouze elementární úpravy přičtení 𝛼-násobku i-tého řádku k j-tému, kde i < j.
• Matice U je výsledný odstupňovaný tvar A, spolu s hodnotami pivotů.

Nechť jsou R₁, ..., R_k matice techto elementárních úprav, které převedou PA v U. Platí maticová rovnost
R_kR_k-1⋯R₂R₁PA = U.
Matice úprav R_i jsou dolní trojúhelníkové matice s jednotkovou diagonálou. Proto je L = (R_kR_k-1⋯R₂R₁)^-1 také dolní trojúhelníková matice s jednotkovou diagonálou. Získáváme dekompozici PA=LU.

Poznámka: Pokud je matice A symetrická a lze ji eliminovat bez prohazování řádků, má její LDU dekompozice speciální symetrickou formu A = LDL^T.

Tagy: #klicove

Hodnost matice

Hodnost matice A se značí rank(A) a udává, jak moc je matice A blízká regulární matici. Několik ekvivalentních definic rank(A):

• dim Im(A), což je počet lineárně nezávislých sloupců matice a také dimenze obrazu příslušného lineárního zobrazení.
• dim R(A), neboli počet lineárně nezávislých řádků matice.
• počet nenulových řádků a počet pivotů v odstupňovaném tvaru A.
• nejmenší počet matic hodnosti jedna, jejichž součet je A.

Pro hodnost platí následující horní odhady:

• rank(A) ≤ min {m,n} pro matici A velikosti m x n.
• rank(A+B) ≤ rank(A) + rank(B).
• rank(AB) ≤ min {rank(A), rank(B)}.

Poslední nerovnost má následující důkaz v řeči lineárních zobrazení:
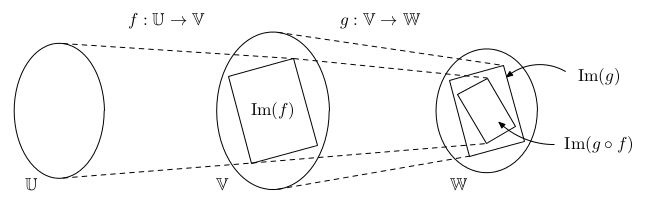Tvrzení: Násobení regulární maticí zleva/zprava nemění hodnost.

Důkaz: Dokažme pro násobení zleva. Podle nerovnosti je rank(RA) ≤ rank(A). Na druhou stranu, protože R je regulární, A = R^-1RA. Tedy rank(A) = rank(R^-1RA) ≤ rank(RA).

Duální zobrazení

K lineárnímu zobrazení f : U ⟶ V je přiřazeno duální zobrazení f^* : V ⟶ U, které má speciální vlastnosti. Povšimněme si, že inverzní zobrazeni f^-1 : V ⟶ U zobrazuje mezi stejnými prostory (pokud existuje), avšak duální zobrazení je něco zcela jiného (například vždy existuje).

Definice přes skalární součin: Duální zobrazení f^* : V ⟶ U je jediné zobrazení, které pro libovolné vektory x∊U a y∊V splňuje:
⟨f(x) | y⟩ = ⟨x | f^*(y)⟩.
Povšimněme si, že levá strana rovnosti je skalární součin ve V, zatímco pravá v U.

Nechť A reprezentuje f vůči bázím X a Y. Pro standardní skalární součin je f^* reprezentováno A^T. Tedy transpozice odpovídá dualitě.

Pro jaké báze reprezentuje A^T zobrazení f^*? Souřadnice bází X a Y můžeme popsat vůči kanonickým bázím maticemi přechodu X a Y (tedy jejich sloupcové vektory jsou souřadnice bazických vektorů).

Tvrzení: Pro standardní skalární součin je zobrazení f^* jednoznačně určené a reprezentuje ho matice A^T vůči duálním bázím Y^* a X^*, což jsou sloupcové vektory Y^-T a X^-T.

Důkaz: Dokažme to nejprve vůči kanonickým bázím. Nechť B je matice splňující ⟨Ax | y⟩ = ⟨x | By⟩. Zjevně pro B = A^T to platí. Je to jediná taková matice, protože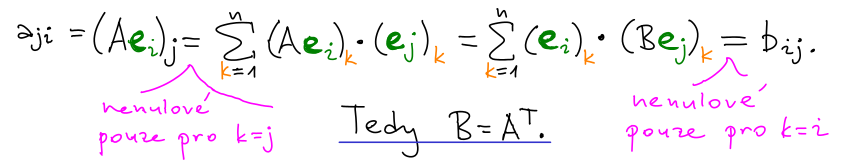
Pro obecné báze to platí z následujícího důvodu. Matice Y^-1AX reprezentuje f vůči kanonické bázi. Proto duální zobrazení f^* je reprezentováno (Y^-1AX)^T = X^TA^TY^-T vůči kanonické bázi.

Soustavy lineárních rovnic: Ax=b

Začneme příkladem soustava tří lineárních rovnic o třech neznámých: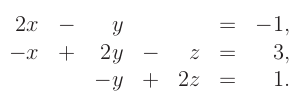
Hledáme množinu všech řešení, což jsou trojice (x,y,z), které po dosazení splňují všechny tři rovnice současně. V tomto případě je řešením jediná trojice (1,3,2).

Obecně soustava m lineárních rovnic o n neznámých:


Čísla a_i,j a b_j jsou pevně zadaná a nazývají se koeficienty. Čísla x_j se nazývají neznámé a jejich hodnoty chceme nalézt.

Hledáme množinu řešení tvořenou n-ticemi (x₁,...x_n) takovými, že po dosazení budou zároveň splněny všechny rovnice.

Tagy: #klicove

Permutační matice

Nechť 𝜋 je permutace množiny {1,...,n}. Je reprezentována permutační maticí P. To je čtvercová matice n x n, jejíž koeficienty jsou nuly a jedničky, a
(P)_i,j = 1, právě když 𝜋(i)=j.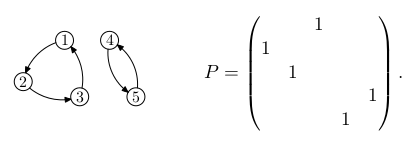 Nechť A je libovolná matice, kterou násobíme permutační maticí P.

• Násobení zprava permutuje řádky A podle 𝜋.
• Násobení zleva permutuje sloupce A podle 𝜋^-1.

Nechť P_𝜋 značí permutační matici reprezentující 𝜋. Čtenář si může rozmyslet a dokázat následující vlastnosti.

Součin permutačních je permutační matice, která reprezentuje složení příslušných permutací. Tedy
P_𝜋P_𝜎 = P_𝜋∘𝜎.
Každá permutační matice P je regulární, dokonce ortogonální, tedy existuje inverzní matice, která je také permutační. Pro ni platí, že
P_𝜋^-1 = P_𝜋^-1 = P_𝜋^T. Snadné je přímo z definice ověřit, že tato inverze je oboustranná.

Permutační matice tvoří grupu. Podle Cayleyho věty je možné libovolnou grupu o n prvcích reprezentovat jako grupu permutací {1,...,n}. Proto je možné libovolnou grupu o n prvcích reprezentovat permutačními maticemi n x n. To přirozeně vede ke zkoumání pojmu maticových grup.

Trojúhelníkové matice

Rozlišujeme dva druhy trojúhelníkových matic. Typicky se uvažují čtvercové matice, ale definice funguje i pro obdélníkové.

Dolní trojúhelníková matice L má všechny koeficienty nad hlavní diagonálou nulové. Tedy (L)_i,j = 0 pro i > j.

Horní trojúhelníková matice U má všechny koeficienty pod hlavní diagonálou nulové. Tedy (U)_i,j = 0 pro i < j.


Diagonální matice jsou současně dolní a horní trojúhelníkové.

Nechť horní trojúhelníková matice U reprezentuje zobrazení vůči jedné bázi b₁,...,b_n. Protože Ub_i leží v ⟨b₁,...,b_i⟩ (a podobně pro dolní trojúhelníkové matice L), je celá řada problému s trojúhelníkovými maticemi výrazně jednodušších. Například soustavy Lx = b a Ux = b lze řešit přímo substitucí. Je také jednoduché najít inverzní matice a určit vlastní čísla (prvky na diagonále).

Čtenář si může rozmyslet následující vlastnosti:

• Trojúhelníkové matice jsou uzavřené na součin. Tedy součin dolních trojúhelníkových matic je dolní trojúhelníková matice a podobně pro horní trojúhelníkové matice.
• Trojúhelníková matice je regulární právě tehdy, když jsou koeficienty na diagonále nenulové.
• Trojúhelníkové matice jsou uzavřené na inverze. Tedy inverzí dolní trojúhelníkové matice je dolní trojúhelníková matice, inverzí horní trojúhelníkové je horní trojúhelníková.
• Přímo z definice si můzeme rozmyslet, že čtvercová trojúhelníková matice má inverzi z jedné strany, právě když ji má z druhé strany. To je důležité pro důkaz obecné věty o oboustranné inverzi pomocí LU dekompozice.

Transpozice

Nechť A je matice m x n. Její transpozice A^T je matice n x m s následujícími koeficienty:

(A^T)_i,j = (A)_j,i.

Tedy koeficienty matice A^T vzniknou zrcadlením koeficientů A podle hlavní diagonály.

Pro matice s komplexními čísly se transpozice definuje jinak. Značí se A^H a čísla jsou navíc komplexně sdružená (což odpovídá jinému skalárnímu součinu). Transpozice se často také značí A^* (jak reálná, tak komplexní).

Pro transponované matice platí následující vztahy, rozmyslete si jejich důkazy z definice maticových operací:

• (A^T)^T = A.
• (cA)^T = cA^T.
• (A+B)^T = A^T+B^T.
• (AB)^T = B^TA^T. Povšimněme si, že pořadí transponovaných matic musí být obrácené, aby měl součin kompatibilní rozměry. Jak vypadá transpozice obecně pro součin více matic?
• Pokud je A regulární matice, pak (A^-1)^T = (A^T)^-1 = A^-T.

Fundamentální podprostory

Nechť A je matice m x n s řádkovými vektory r₁, ..., r_m a sloupcovými vektory s₁, ..., s_n. Matice A definuje čtyři fundamentální podprostory:

• Jádro Ker(A) = {x : Ax = 0} (neboli kernel).
• Řádkový prostor R(A) = Im(A^T) = ⟨r₁, ..., r_m⟩ = {A^Tx : x∊ℝ^m} (neboli levý obraz).
• Levé jádro Ker(A^T) = {y : y^TA = 0} (neboli levý kernel).
• Sloupcový prostor S(A) = Im(A) = ⟨s₁, ..., s_n⟩ = {Ax : x∊ℝ^m} (neboli obraz).

Povšimněme si, že jádro a řádkový prostor jsou podprostory ℝⁿ, zatímco levé jádro a sloupcový prostor jsou podprostory ℝ^m.

Fundamentální věta lineární algebry:

1. Nechť r = rank(A). Platí, že
   dim R(A) = dim Im(A) = r, dim Ker(A) = n-r a dim Ker(A^T) = m-r.
2. R(A) a Ker(A) jsou lineárně nezávislé a generují ℝⁿ. Podobně Im(A) a Ker(A^T) jsou lineárně nezávislé a generují ℝ^m.
3. Navíc jsou R(A) a Ker(A) ortogonální doplňky, tedy každý vektor z R(A) je kolmý na každý vektor z Ker(A). Podobně pro Im(A) a Ker(A^T).

Poznamenejme, že vlastnost 1 platí nad obecným algebraickým tělesem. Vlastnosti 2 a 3 vyžadují ℝ (a při drobné změně definic fungují i nad ℂ).

Tagy: #klicove

Determinant

Blokové matice

Blokové matice jsou tvořené menšími maticemi, které se nazývají bloky. Můžeme definovat operace na blokových maticích kompatibilního typu. To umožňuje využívat blokový jazyk k efektivnímu popisu některých věcí.

Nechť A a B jsou dvě blokové matice velikosti 2n x 2n, tvořené čtyřmi bloky velikosti n x n.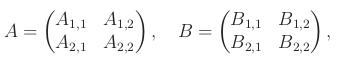
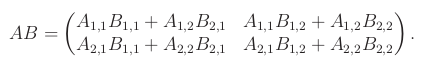
Tyto matice lze sčítat po blocích a násobit po blocích: Čtenář si může rozmyslet, za jakých podmínek lze definovat operace obecně. Také lze definovat blokově diagonální matice, blokově trojúhelníkové matice, atd.

Blokové násobení se prakticky využívá při násobení velkých matic. Pro ně je potřeba číst koeficienty z paměti (řekněme RAM), která je mnohem pomalejší než rychlost výpočtů počítače. Řekněme, že násobíme matice velikosti n x n a do paměti dokážeme naráz načíst zhruba 2b² koeficientů.

Pokud budeme postupovat podle definice, tak vždy určíme jeden koeficient AB vynásobením koeficientů řádku A a sloupce B. Na to potřebujeme udělat n/b² čtení z paměti, tedy celkem n³/b² součinů.

Místo toho rozdělíme obě matice na bloky b x b (pro jednoduchost nechť n je násobek b). Pro výpočet hodnot jednoho bloku AB musíme vynásobit jeden řádek bloků A s jeden sloupcem bloků B. Na to potřebujeme udělat n/b čtení. Bloků AB je n²/b², tedy dohromady děláme n³/b³ čtení, což je b-krát efektivnější.

Hodnost 1

Matice A má hodnost 1, pokud je nenulová a každý její řádek/sloupec je násobek ostatních. Existuje elegantní zápis

A = xy^T,

kde x a y jsou nenulové vektory.

Fundamentální podprostory

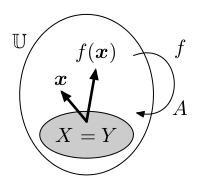
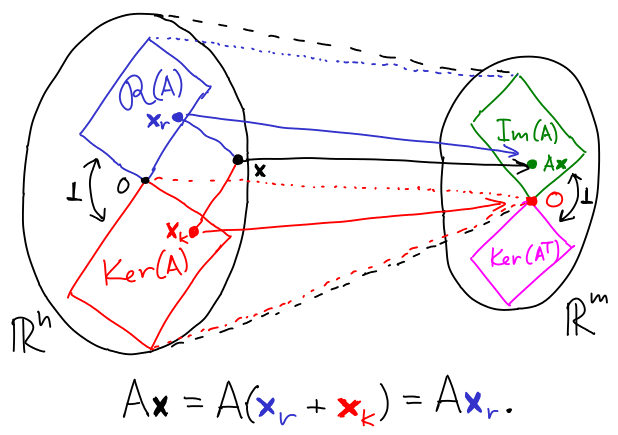
Lineární zobrazení f : U ⟶ V definuje dva fundamentální podprostory:

• Jádro Ker(f) = {x : f(x) = 0} (neboli kernel).
• Obraz Im(f) = {f(x) : x∊U}.

Jádro je podprostor U, zatímco obraz je podprostor V. Pokud matice A reprezentuje f, tyto podprostory odpovídají Ker(A) a Im(A).

Čemu však odpovídají zbývající dva fundamentální podprostory A? Jsou to jádro a obraz duálního zobrazení f^* : V ⟶ U.

• Levé jádro Ker(f^*) = {x : f^*(x) = 0} (neboli levý kernel).
• Levý obraz Im(f^*) = {f^*(x) : x∊U}.

Na obrázku je naznačeno duální zobrazení spolu se svými fundamentálními podprostory.

Speciální matice

Některé druhy matic se objevují v lineární algebře často, že se pro ně vyplatí mít speciální jména.

Jsou zajímavé ze dvou důvodu:

1. Vyskytují se často v lineární algebře a v různých aplikacích.
2. Mají speciální vlastnosti, kterých lze využít například při výpočtech či strukturální analýze.

Diagonální matice

Diagonální matice D má všechny koeficienty mimo hlavní diagonálu nulové, tedy (D)_i,j = 0 pro i ≠ j. Definice funguje i pro obdelníkové matice.

Jednotková matice I_n je diagonální matice n x n s jedničkami na diagonále.

Pokud reprezentují endomorfismus vůči jedné bázi, odpovídají natažení souřadních os. V případě jednotkové matice se jedná o identitu.

Tvrzení: Libovolné lineární zobrazení f je reprezentováno vůči vhodným bázím X a Y diagonální maticí, která má na diagonále pouze 1 a 0.

Důkaz: Nechť X_r je libovolná báze levého obrazu Im(f^*) a X_k je libovolná báze jádra Ker(f). Zvolíme X = X_r ∪ X_k.

Protože f definuje izomorfismus mezi Im(f^*) a Im(f), zobrazuje libovolnou bázi Im(f^*) na bázi Im(f). Tedy f(X_r) je báze Im(f), kterou doplníme bází Ker(f^*) a získáme druhou hledanou bázi Y. Protože f(X_k) = {0}, je zobrazení f reprezentováno vůči X a Y popsanou diagonální matici.

Tvrzení: Čtvercová matice A komutuje s každou čtvercovou maticí, právě když A=cI_n.

Pozitivně definitní matice

Čtvercová symetrická matice A se nazývá pozitivně definitní, právě když platí jedna z následujících šesti ekvivalentních vlastností:

1. Pro každé x ≠ 0 je x^TAx > 0.
2. Všechna vlastní čísla 𝜆_i > 0. (Vlastní čísla jsou reálná ze symetrie A.)
3. Determinanty principiálních minorů det(A₁), ..., det(A_n) > 0. Principiální minor A_k je čtvercová podmatice A velikosti k x k v levém rohu.
4. Lze provést Gaussovu eliminaci bez prohazování a násobení řádků a všechny pivoty p_i > 0.
5. Existuje regulární matice R taková, že A = R^TR, což je Choleského rozklad.
6. Výraz x^TAy je skalární součin a √x^TAy je norma.

Tvrzení: Pro symetrické matice A jsou vlastnosti 1 až 6 ekvivalentní.

Skalární součin

Skalární součin lze definovat konkrétně formulí nebo abstraktně pomocí vlastností.

Standardní skalární součin je definován výrazem
⟨x | y⟩ = x^Ty = ∑ x_iy_i = x₁y₁ + ⋯ + x_ny_n.
Abstaktní definice popisuje skalární součin jako libovolné zobrazení ℝⁿ ⨯ ℝⁿ ⟶ ℝ splňující vlastnosti:

1. Linearita: ∀ x, y, z ∊ ℝⁿ: ⟨x+y | z⟩ = ⟨x | z⟩ + ⟨y | z⟩.
   ∀ x, y ∊ ℝⁿ, 𝛼 ∊ ℝ: ⟨𝛼*x | y⟩ = 𝛼*⟨x | y⟩.
2. Symetrie: ∀ x, y ∊ ℝⁿ: ⟨x | y⟩ = ⟨y | x⟩.
3. Pozitivní definitnost: ∀ x ∊ ℝⁿ, x ≠ 0: ⟨x | x⟩ > 0.
   (Poznámka: Pro x = 0 je ⟨x | x⟩ = 0 z linearity.)

Libovolné zobrazení splňující první vlastnost (v obou složkách) se nazýva bilineární forma, dvojicím vektorů přiřazuje reálná čísla a je lineární v obou složkách. Tedy skalární součin je symetrická pozitivně definitní bilineární forma. Rozmyslete si, že standardní skalární součin vlastnosti 1 až 3 splňuje.

Nad tělesem komplexních čísel ℂ se komplexně sdružuje: Standardní skalární součin má komplexně sdružené koeficienty x. Abstraktní skalární součin má ve vlastnosti 2 komplexní sdružení.

Skalární součin (třeba standardní) je možné definovat stejně i nad obecnými algebraickými tělesy, ale pozitivní definitnost nemůže být splněna (nad obecným tělesem dokonce nerovnost nedává smysl). Tedy skalární součin je výrazně slabší pojem nad obecnými tělesy.

Výraz x^Ty lze přirozeným způsobem zobecnit na x^TAy, kde A je nějaká matice. V příkladu 1 je potřeba kvůli třetí vlastnosti, aby každé c_i bylo kladné. V příkladu 2 lze vlastnost 3 dokázat převodem na součet čtverců:
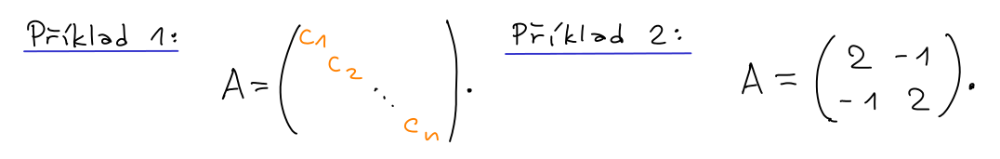
⟨x | x⟩ = 2x₁² - 2x₁x₂ + 2x₂² = x₁² + x₂² + (x₁ - x₂)² > 0.
Výraz x^TAy je obecně bilineární forma.

• Pokud je matice A symetrická, je to symetrická bilineární forma.
• Pokud je A navíc pozitivně definitní (∀ x ≠ 0: x^TAx > 0), je to symetrická pozitivně definitní bilineární forma, neboli skalární součin.

Věta: Libovolný skalární součin ⟨x | y⟩ je roven x^TAy, kde A je nějaká symetrická pozitivně definitní matice.

Důkaz: Nechť e₁, ..., e_n je kanonická báze. Z linearity je skalární součin jednoznačně určený hodnotami pro libovolnou bázi:
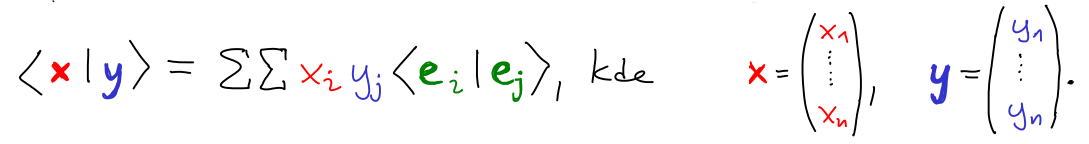
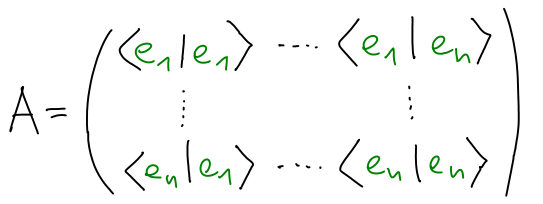Jako A zvolíme Gramovu matici tvořenou skalárními součiny ⟨e_i | e_j⟩. Potom je ⟨x | y⟩ = x^TAy. Z vlastností 2 a 3 skalárního součinu vyplývá, že A je symetrická pozitivně definitní matice.

Kvadratické formy a definitnost

Ortogonální matice

Matice Q se nazývá ortogonální, pokud má ortonormální sloupce (ortogonalita + normy rovné jedné). V maticovém zápisu dostáváme Q^TQ = I_n.

Tedy pro ortogonální matice platí, že Q^-1 = Q^T. Protože inverze libovolné čtvercové matice je oboustranná, dostáváme navíc, že QQ^T = I_n. Tedy pokud má čtvercová matice ortonormální sloupce, má také ortonormální řádky, a také matice Q^T je ortogonální.

Skalární součin, norma a kolmost

Cíl je nad vektorovým prostorem ℝⁿ zavést další geometrické pojmy.

• Skalární součin ⟨x | y⟩ dvou vektorů x a y popisuje, jak moc ukazují společným směrem a souvisí s úhlem, které vektory svírají.
• Kolmé vektory (neboli ortogonální vektory) nemají žádný společný směr, což je právě tehdy, když ⟨x | y⟩ = 0.
• Norma ∥x∥ je geometrická délka vektoru.

V matematice se často objevují prostory prvků (nemusí být vektorové prostory) obohacené nějakými geometrickými vlastnostmi. Dostáváme následující hierarchii možných geometrii:

skalární součin ⇒ norma ⇒ metrika ⇒ topologie.
Například prostor může být povrch koule, na kterém můžeme uvažovat geometrické vzdálenosti. Z těchto definic lze uvažovat topologii a metriku, ale nemůžeme definovat skalární součin a normu.

• Prostor se skalárním součinem. Nad prostorem lze uvažovat úhly a kolmost. Existence skalárního součinu indukuje normu: ∥x∥ = √⟨x | x⟩.
• Prostor s normou. Nad prostorem lze uvažovat vzdálenosti, které se chovají lineárně vůči natahování vektorů: ∥c*x∥ = |c|*∥x∥. Norma indukuje metriku 𝜌(x,y) = ∥x-y∥.
• Prostor s metrikou. Metrika je funkce vzdálenosti 𝜌(x,y), která je nezáporná (a kladná pro x ≠ y), symetrická a splňuje trojúhelníkovou nerovnost. Oproti normě nemusí mít prostor strukturu vektorového prostoru, tedy nemusí platit linearita. Norma indukuje topologii pomocí otevřených a uzavřených 𝜀-okolí, což jsou množiny B_𝜀(x) = {y : 𝜌(x,y) ≤ 𝜀} (případně s ostrou nerovností).
• Prostor s topologií. Nemáme přímo definovanou vzdálenost, ale topologie popisuje blízkost. To se dělá pomocí systému uzavřených a otevřených okolí. Výhoda je, že v řadě situací vzdálenost vůbec nepotřebujeme. Nad topologickými prostory lze dělat velkou část analýzy. Například můžeme definovat limitu posloupnosti: lim x_n = x, pokud pro každé otevřené okolí bodu x existuje N > 0 takové, že pro n > N leží každé x_n v tomto okolí x.

Symetrické matice

Čtvercová matice A se nazývá symetrická, pokud platí A=A^T. Symetrické matice reprezentují endomorfismy, které jsou sami sobě duální.

Symetrické matice řadu speciálních vlastností, například jsou uzavřené na součiny a inverze.

Ortonormální báze

Z lineární nezávislosti ortogonálních vektorů má pojem ortogonální báze smysl. Typicky navíc máme ortonormální s jednotkovou normou: není to klíčové, ale zjednodušuje to vzorce.

Tvrzení: Libovolnou ortogonální/ortonormální množinu nenulových vektorů lze rozšířit na ortogonální/ortonormální bázi.

Důkaz: Doplníme ortonormální množinu na libovolnou bázi a aplikujeme Gram-Schmidtovu ortogonalizaci. Alternativní důkaz je možný přes fundamentální větu lineární algebry.

Tedy ortogonálních bází je spousta a jsou to hezké báze, mající řadu skvělých vlastností.

1. Ortonormální báze mají výhodné numerické vlastnosti.
2. Snadný výpočet souřadnic pomocí ortogonálních projekcí. Pro obecnou bázi je to řešení soustavy lineárních rovnic A𝛼 = x. Pro ortogonální bázi v₁, ..., v_n je
Důkaz vyplývá z ortogonality: ⟨x | v_i⟩ = ⟨𝛼₁v₁ + ⋯ + 𝛼_nv_n | v_i⟩ = 𝛼_i*⟨v_i | v_i⟩.

Jiný pohled je přes ortogonální matice: 𝛼 = Q^TQ𝛼 = Q^Tx, pokud sloupce Q jsou ortonormální vektory v₁, ..., v_n.

Norma

Norma ∥x∥ je geometrická délka vektoru x. Opět má různé definice.

Norma indukovaná skalárním součinem. Libovolný skalární součin ⟨x | y⟩ definuje normu ∥x∥ = √⟨x | x⟩. Například standardní skalární součin definuje standardní normu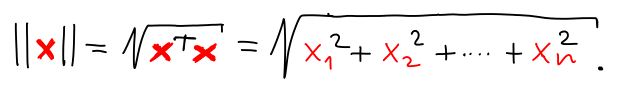
Vlastnosti 1 a 3 vyplývají z příslušných vlastností skalárního součinu. Pro trojúhelníkovou nerovnost:
Abstaktní definice popisuje normu jako libovolné zobrazení ℝⁿ ⟶ ℝ splňující vlastnosti:

1. Linearita: ∀ x ∊ ℝⁿ, 𝛼 ∊ ℝ: ∥𝛼*x∥ = 𝛼|*∥x∥.
2. Trojúhelníková nerovnost: ∀ x, y ∊ ℝⁿ: ∥x+y∥ ≤ ∥x∥ + ∥y∥.
3. Nezápornost: ∀ x ∊ ℝⁿ, x ≠ 0: ∥x∥ > 0.
   (Poznámka: Pro x = 0 je ∥x∥ = 0 z linearity.)

Ortogonální doplněk

Nechť U je libovolný vektorový podprostor. Ortogonální doplněk U je množina

U^⊥ = {x : x ⊥ y pro každé y ∊ U}.
Tvrzení: Ortogonální doplněk U^⊥ má následující vlastnosti:

1. U^⊥ je vektorový podprostor.
2. U ∩ U^⊥ = {0} a ⟨U ∪ U^⊥⟩ = ℝⁿ.
3. dim U + dim U^⊥ = n.
4. (U^⊥)^⊥ = U.

Důkaz: Vlastnosti 1 a první část 2 jsou jednoduché. Pro zbytek potřebujeme existenci ortogonálních bází. Zvolme ortogonální bázi b₁, ..., b_k prostoru U a doplňme ji vektory b_k+1, ..., b_n na ortogonální bázi ℝⁿ. Vektory b_k+1, ..., b_n tvoří ortogonální bázi U^⊥. Pokud totiž nějaký vektor má nenulovou souřadnici vůči b₁, ..., b_k, nemůže ležet v U^⊥.

Fundamentální podprostory matice A jsou svoje ortogonální doplňky:

Ker(A) = R(A)^⊥,  Ker(A^T) = Im(A)^⊥.
Důkaz: Nechť x ∊ Ker(A) a u₁, ..., u_m jsou řádky matice A. Z definice je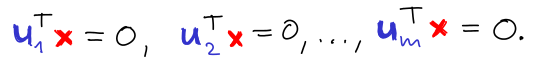
Tedy x je ortogonální na R(A), a naopak libovolný ortogonální vektor na R(A) patří do Ker(A). Proto je Ker(A) = R(A)^⊥. Druhá rovnost se získá pro A^T.

Cauchy-Schwarzova nerovnost

Věta: (Cauchy-Schwarz) Pro libovolné vektory x a y platí nerovnost

|⟨x | y⟩| ≤ ∥x∥*∥y∥.
Poznámka: Věta má následující aplikaci ve funkcionální analýze. Na prostoru funkcí můžeme definovat skalární součin a příslušnou indukovanou normu, například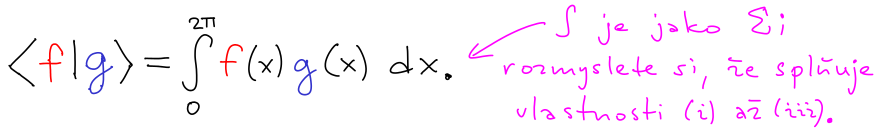
Protože se chceme vyhnout nekonečným hodnotám, můžeme uvažovat Hilbertův podprostor všech funkcí, které mají konečnou normu. Podle Cauchy-Schwarzovy věty jsou i jejich skalární součiny konečné.

Cosinová věta: Pro libovolné vektory x a y svírající úhel 𝜑 platí, že

⟨x | y⟩ = ∥x∥*∥y∥*cos(𝜑).
Skalární součin je kladný pro ostrý úhel 𝜑, nulový pro kolmý úhel 𝜑 a záporný pro tupý úhel 𝜑.

Uvažme kolmou projekci p vektoru x na vektor y. Platí, že norma ∥e∥ rozdílu projekce a vektoru e = p - x je nezáporná. Úpravou získáváme Cauchy-Schwarzovu nerovnost:

Charakterizace norem ℝ n

Podle charakterizace jsou normy indukované skalárním součinem tzv. A-normy ∥x∥_A = √x^TAx, kde A je symetrická pozitivně definitní matice. Norem však existuje mnohem víc než skalárních součinů.

Uvažme pro danou normu jednotkovou sféru S a kouli B:

S = {x : ∥x∥ = 1},  B = {x : ∥x∥ ≤ 1}.
Geometrické vlastnosti sféry a koule. Z axiomů normy můžeme vyvodit geometrické vlastnosti S a B.

• Množina S protíná každou přímku procházející počátkem přesně ve dvou bodech (podle linearity a nezápornosti).
• Množina S je symetrická podle počátku: S = -S (podle linearity se záporným koeficientem), a neobsahuje počátek: 0 ∉ S (podle nezápornosti).
• Množina B je konvexní (nejobtížnější, podle trojúhelníkové nerovnosti).

Klíčové je, že norma je jednoznačně popsaná jednotkovou sférou S. Na libovolném paprsku z počátku má přesně jeden vektor y jednotkovou normu. Norma zbývajících vektorů x paprsku je určena z linearity.

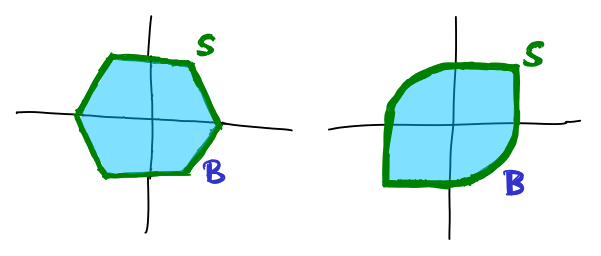Tvrzení: Nechť B je uzavřená omezená podmnožina ℝⁿ, symetrická podle počátku. Nechť S je hranice B a 0 ∉ S. Potom je zobrazení ∥⋅∥ : ℝⁿ ⟶ ℝ, kde

∥x∥ = |𝛼| pro x = 𝛼*y a y ∊ S,
norma.

Tvrzení: Pro normy indukované skalárním součinem je jednotková sféra S pootočený elipsoid, jehož osy jsou vlastní vektory matice A.

Normální matice

Matice A se nazývá normální, pokud komutuje se svoji transpozicí: AA^* = A^*A. Normální matice jsou zobecněním symetrických matic.

Ortogonalita

Vektory x a y jsou ortogonální neboli kolmé, právě když ⟨x | y⟩ = 0. Kolmost značíme x ⊥ y.

Odvození přes Pythagorovu větu. Vektory x a y jsou kolmé, právě když splňují Pythagorovu větu.

Podle definice je počátek 0 kolmý na všechny vektory.

Lemma: Nechť x₁, ..., x_n jsou nenulové po dvou ortogonální vektory, tedy x_i ⊥ x_j pro i ≠ j. Potom jsou vektory x₁, ..., x_n lineárně nezávislé.

Důkaz: Nechť 𝛼₁*x₁ + ⋯ + 𝛼_n*x_n = 0. Chceme dokázat, že všechna 𝛼_i = 0. Vynásobíme-li celý výraz zleva x_i^T, dostáváme z ortogonality

0 = 𝛼₁*x_i^Tx₁ + ⋯ + 𝛼_i*x_i^Tx_i + ⋯ + 𝛼_n*x_i^Tx_n = 𝛼_i*x_i^Tx_i = 𝛼_i*∥x_i∥².
Protože x_i ≠ 0, víme, že 𝛼_i = 0. Protože to platí při násobení libovolným x_i^T, je lineární kombinace 𝛼₁*x₁ + ⋯ + 𝛼_n*x_n triviální.

Kolmost vektorových podprostorů.

QR dekompozice

Gram-Schmidtova ortogonalizace

SVD

Vlastní čísla

Ortogonální projekce

Mějme dva vektory x a y. Chceme nalézt kolmou projekci x na přímku ⟨y⟩. Ekvivalentně je kolmá projekce vektor přímky, který je nejbližší k x.

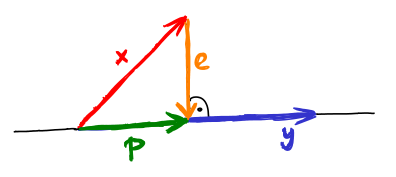
Víme, že p = c*y. Hledáme hodnotu c, aby vektor e = p - x byl kolmý na y: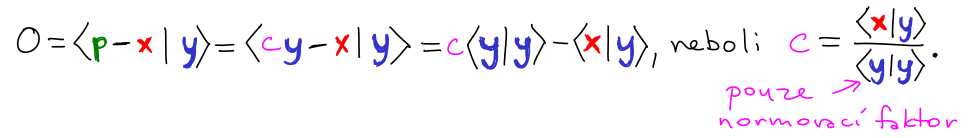

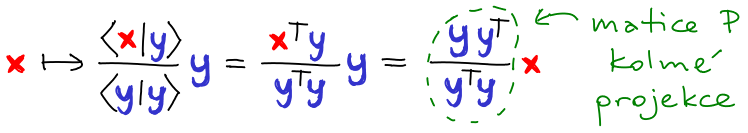
Tvrzení: Kolmá projekce na přímku ⟨y⟩ je lineární zobrazení

Nechť P je matice kolmé projekce na podprostor Im(P). Splňuje dvě následující podmínky:

1. Charakteristika libovolné projekce: P² = P. Projekce je identita na Im(P), tedy Py = y pro libovolné y ∊ Im(P). Protože y = Px pro každé x, získáváme rovnost.

2. Charakteristika kolmosti projekce: P^T = P. Ker(P) je tvořen vektory, které se projektují na 0, což jsou přesně vektory kolmé na Im(P). Tedy Ker(P) = Im(P)^⊥ a z fundamentální věty lineární algebry je Ker(P) = Ker(P^T) a R(P) = Im(P).

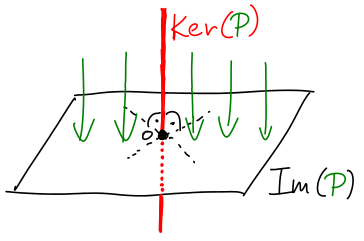
Zbytek plyne z duality, pokud ⟨Px | y⟩ = ⟨x | Py⟩. Zvolme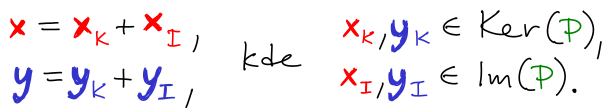
Protože Px = x_I a Py = y_I,

Tvrzení: Pokud sloupce matice A tvoří bázi podprostoru W, je kolmá projekce na W popsána maticí

P = A(A^TA)^-1A^T.

Fourierova transformace

Metoda nejmenších čtverců