Graph isomorphism restricted by lists

Created by Peter Zeman

#mathematics, #presentation

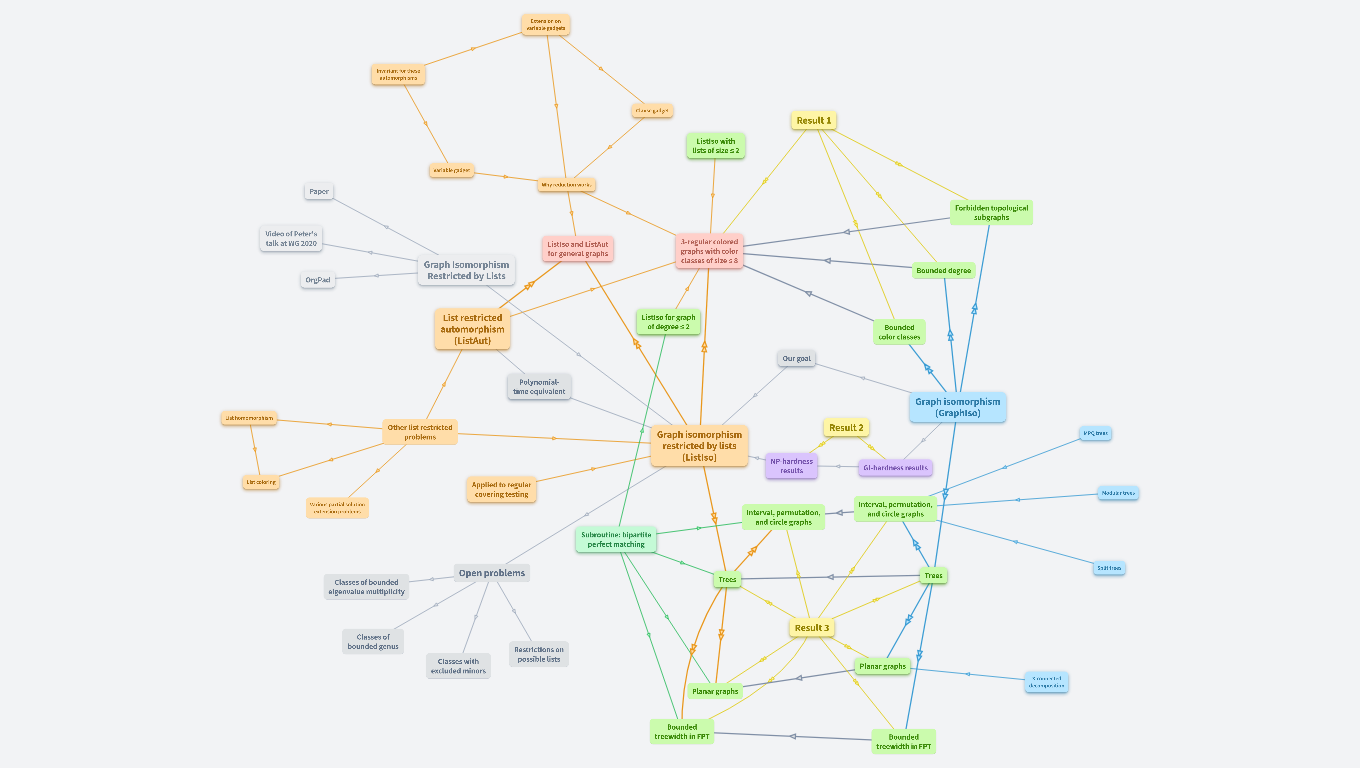
Graph isomorphism restricted by lists

Graph Isomorphism Restricted by Lists

prezentace lidi

WG 2020

Paper

OrgPad

This presentation is created in OrgPad, your all-in-one power tool for brainstorming, idea building and thought processing.

www.orgpad.info

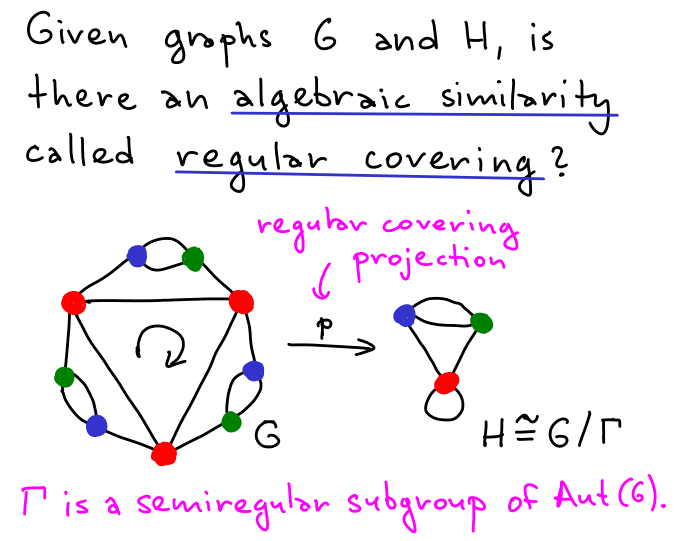
Graph isomorphism (GraphIso)

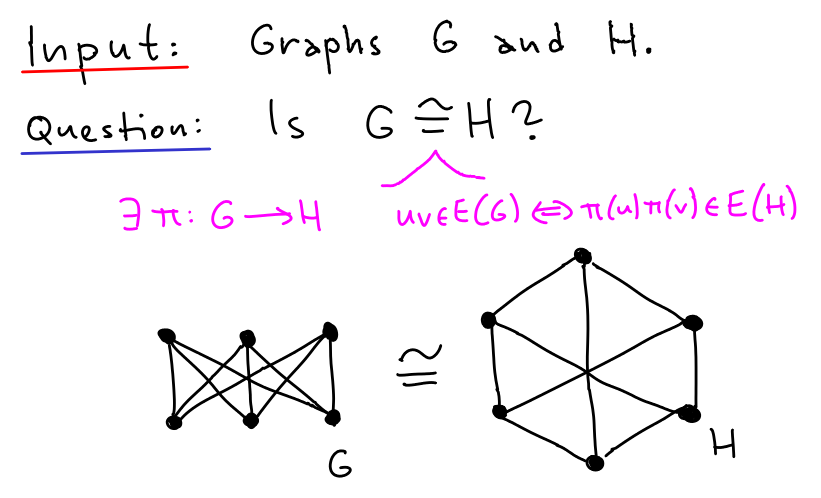
graphiso

graphiso2

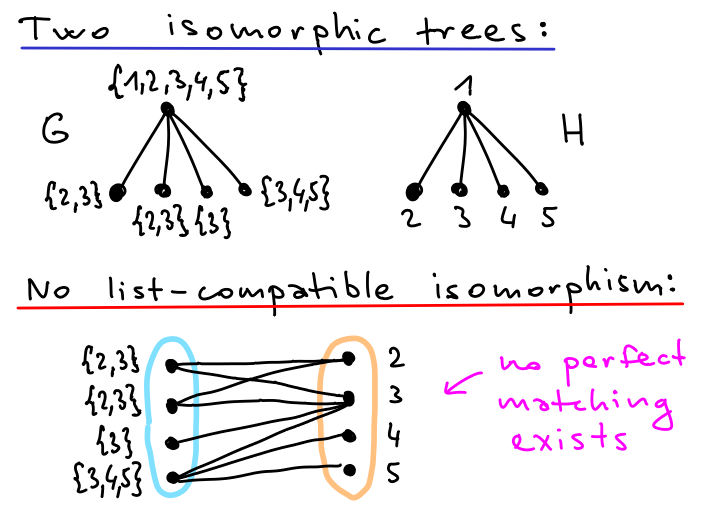
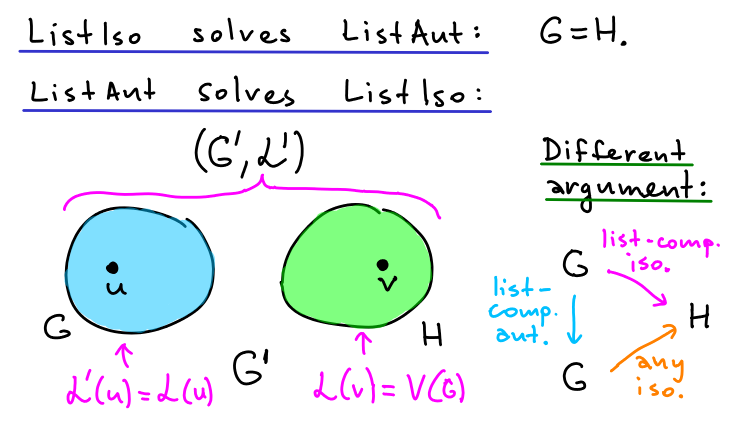
Graph isomorphism restricted by lists (ListIso)

listiso

listiso2

List restricted automorphism (ListAut)

list aut

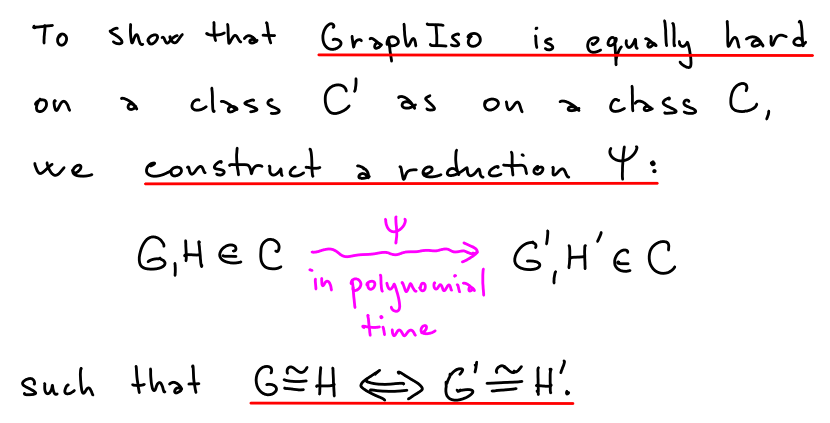
Polynomial-time equivalent

polynomial equivalence

ListIso and ListAut for general graphs

lubiw

Applied to regular covering testing

regular covering

regular covering2

List homomorphism

The same definition, but homomorphism is used instead of isomorphism.

Generalizes list coloring (where the target graph is complete without loops).

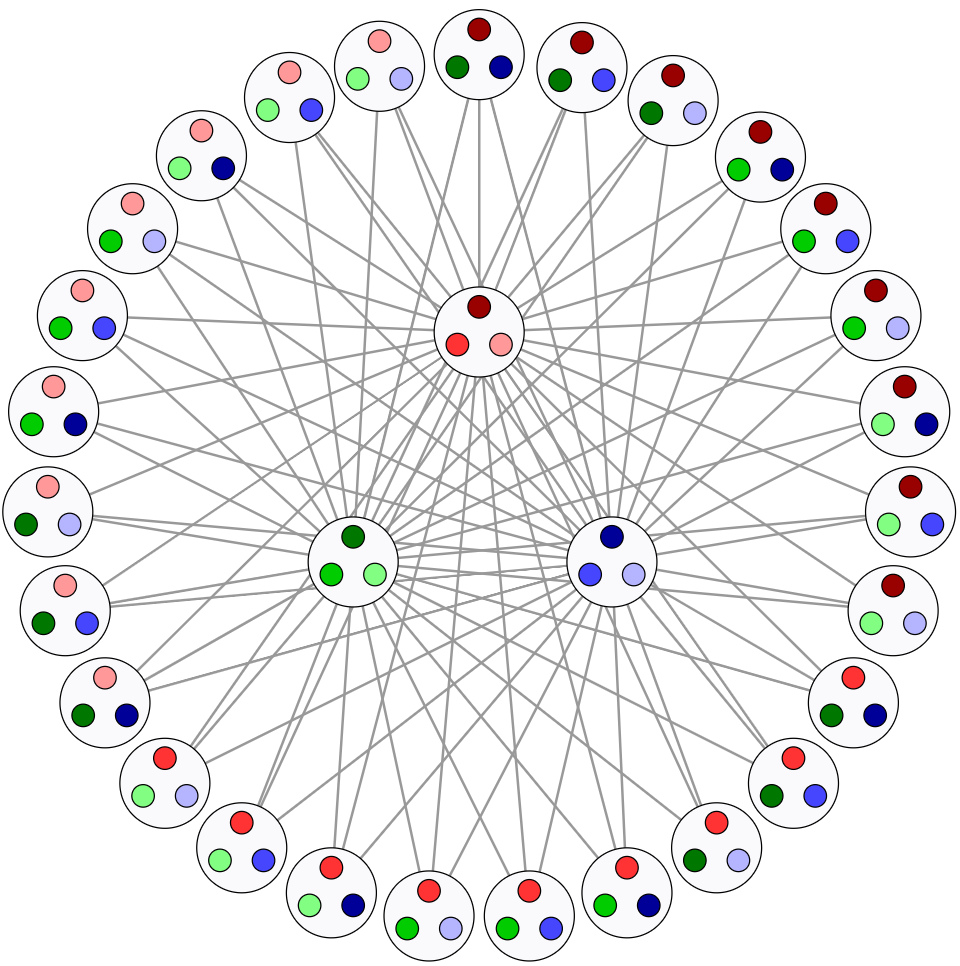
Other list restricted problems

List coloring

Each vertex has a list of permissible colors. We want to find a proper coloring which respects these lists.

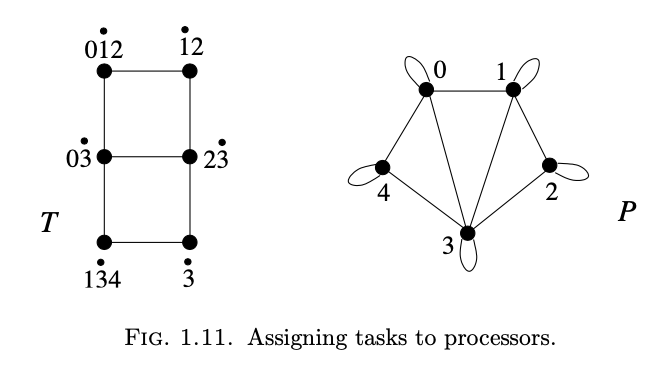
Various partial solution extension problems

Our goal

our goal

Result 1

result3 group theory

ListIso with lists of size ≤ 2

lists of size 2

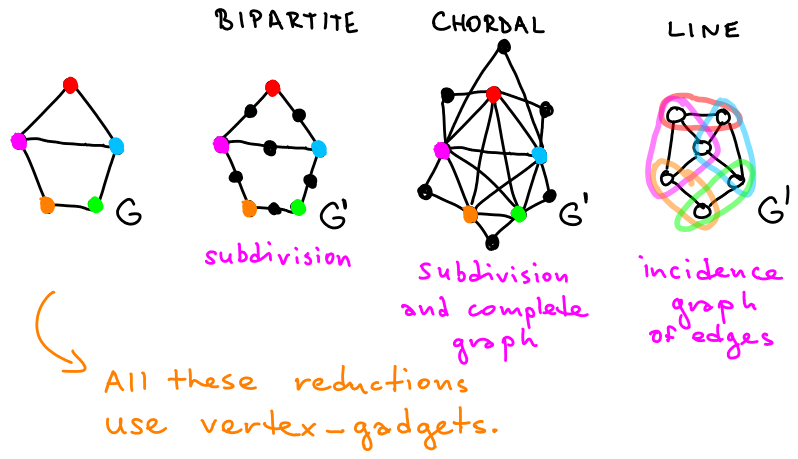
Forbidden topological subgraphs

3-regular colored graphs with color classes of size ≤ 8

3reg NPc

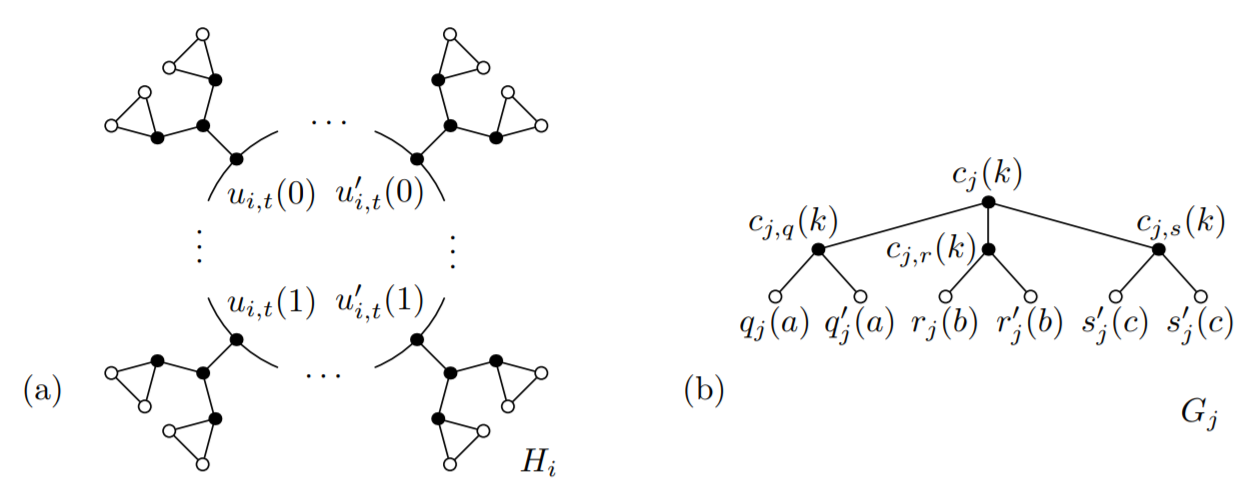
Bounded degree

ListIso for graph of degree ≤ 2

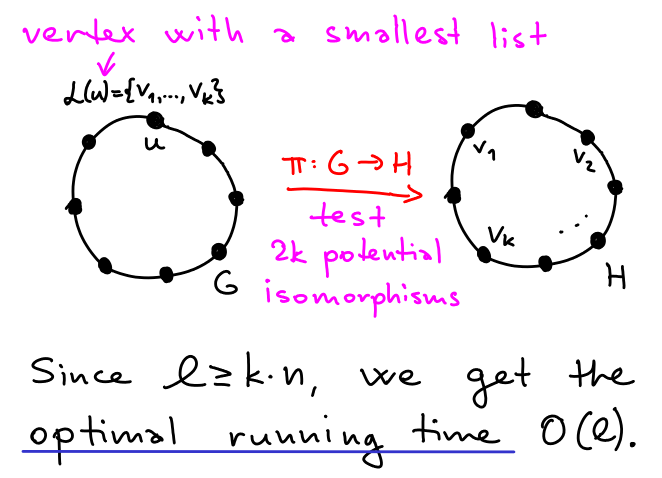
cycles

max degree 2

Bounded color classes

Result 2

result1 gi completeness

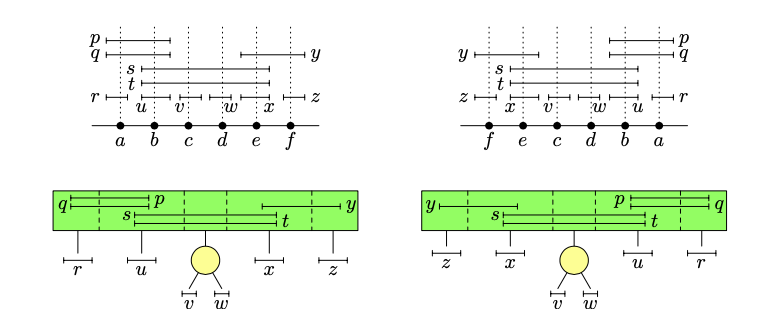
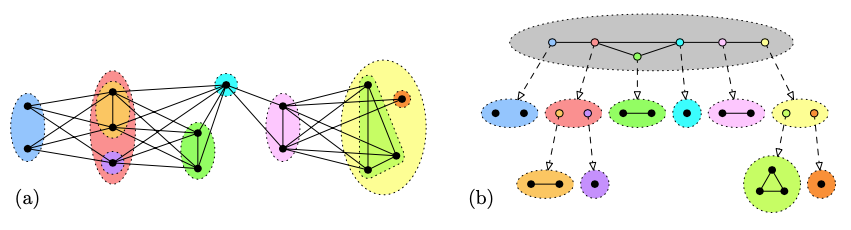
MPQ trees

MPQ tree describes all interval representations:

NP-hardness results

vertex gadget reductions

vertex gadget reductions translate

GI-hardness results

gi hardness

gi hardness2

Interval, permutation, and circle graphs

Modular trees

Modular tree captures all transitive orientations of a graph and all permutation representations.

Interval, permutation, and circle graphs

Subroutine: bipartite perfect matching

Can be solved in O(m • √n) using the algorithm of Hopcroft and Kapr (1973). It is the bottleneck in solving ListIso for various graph classes.

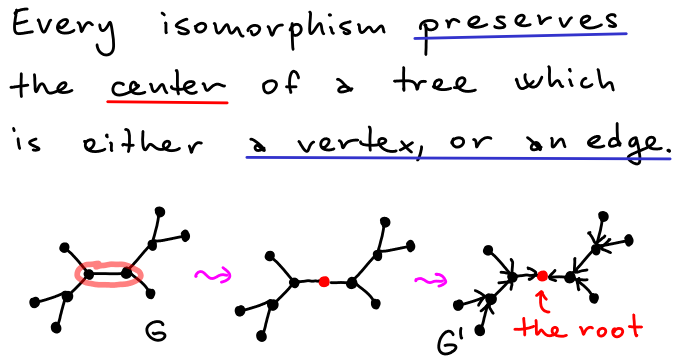
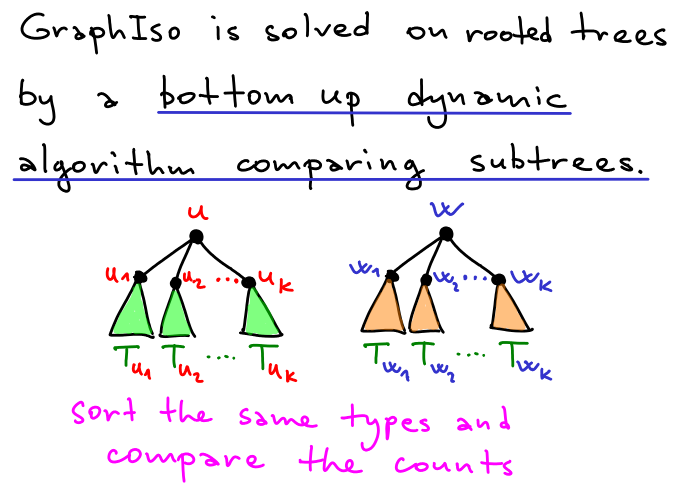
Trees

tree listiso

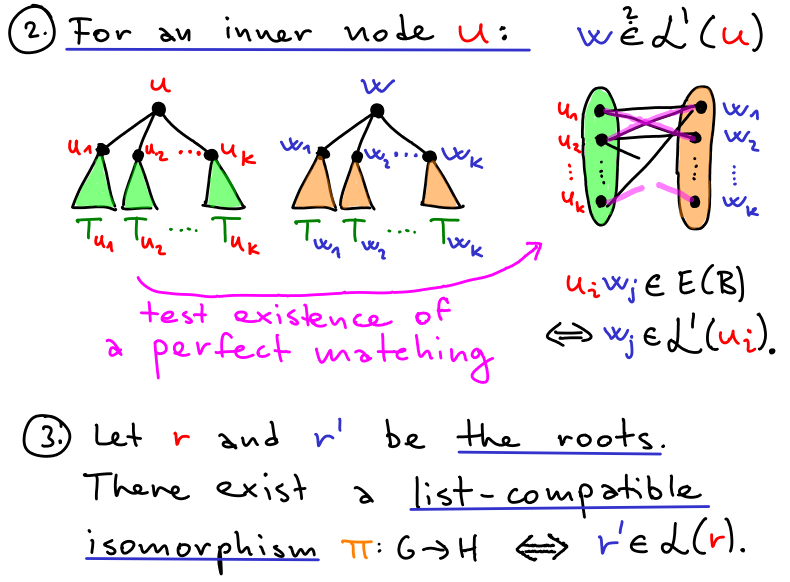
tree listiso2

Trees

tree graphiso

tree graphiso2

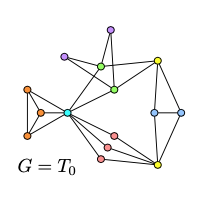
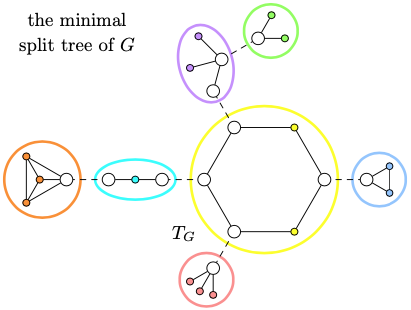
Split trees

Split tree captures all representations of a circle graph.

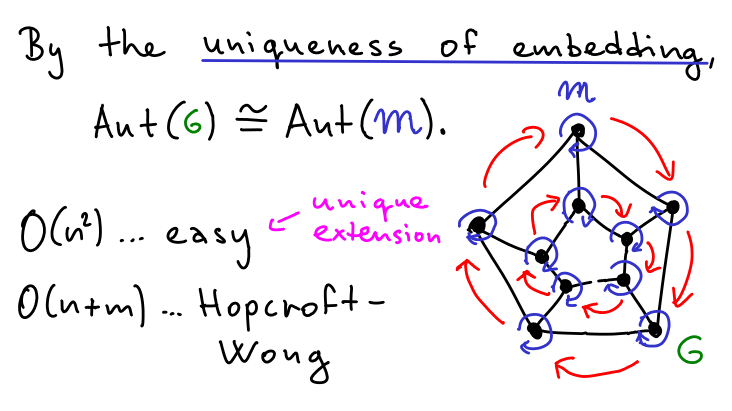
Result 3

result2 combinatorics

Planar graphs

3conn planar graphiso

planar graphiso

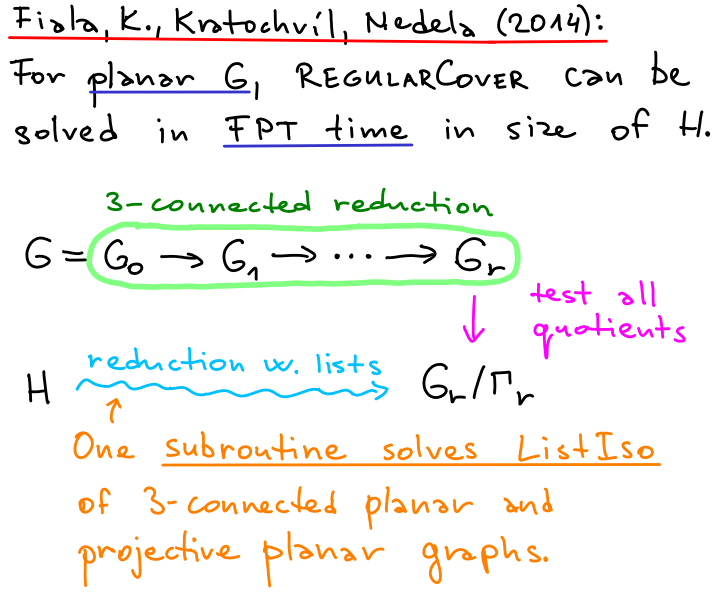
Planar graphs

3-connected decomposition

Mostly known in the literature as SPQR trees.

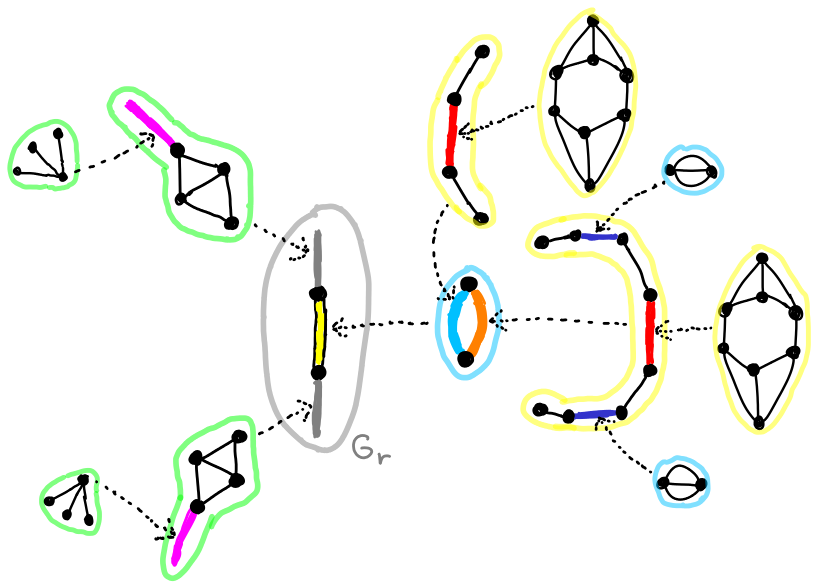
reduction tree

Bounded treewidth in FPT

Bounded treewidth in FPT

Variable gadget

variable gadget

Clause gadget

clause gadget

Why reduction works

lubiw2

Classes of bounded eigenvalue multiplicity

Open problems

Classes of bounded genus

Classes with excluded minors

Restrictions on possible lists

Extension on variable gadgets

clause gadget2

Invariant for these automorphisms

variable gadget2

Video of Peter's talk at WG 2020