Created by Barbora Havířová
Voda v hrnci se ohřívá na sporáku. = vedení + proudění
Teplíčko u táborového ohně. = záření
Je mi zima. = vedení (jen nepatrně záření)
Kovové zábradlí je studené. = vedení
Vzduch v místnosti se ohřívá od topení. = vedení + proudění
ÚLOHA 1:
V elektrické pračce se ohřívá voda o hmotnosti 30 kg.
a) Jaké teplo přijme, zvýší-li se její teplota z 15 °C na 90 °C?
b) Jak dlouho trvá ohřívání, je-li příkon topného tělesa 2,5 kW? Účinnost pračky při ohřívání je 90 %.
ÚLOHA 2:
Do varné konvice s výkonem 2000 W jsme nalili vodu o objemu 1,2 l a teplotě 15 °C. Když se voda začala vařit, konvice vypnula.
a) Jak dlouho by trval ohřev v ideálním případě?
b) Ve skutečnosti byl ohřev asi o 30 s delší, co z toho plyne?
ÚLOHA 1:
Teplo je dějová veličina popisující přenos energie. Těleso nemůže mít teplo, může přijímat nebo odevzdávat teplo.
Teplota je stavová veličina popisující těleso. Těleso má určitou teplotu. Nemůže předat teplotu.
Při předávání tepla se obvykle mění teplota, ale nemusí tomu tak být, pokud se současně koná práce.
př. záhřátí rukou
- přiložení na topení = vedení
- přiblížení vedle topení = záření
- umístění nad topení = proudění
- ponoření do teplé vody = vedení
- vyhřívání na slunci = záření
značka Q
jednotka J (joule) stejně jako energie
neuspořádaně se pohybující částice teplejšího tělesa narážejí na částice studenějšího tělesa a předávají jim část své energie
částice studenějšího tělesa se začnou pohybovat rychleji a částice teplejšího tělesa pomaleji
rychlost přenosu závisí na vazbách mezi částicemi
ÚLOHA 1:
Anglický fyzik J. P. Joule (1818 - 1889) se pokusil určit měrnou tepelnou kapacitu vody. Při svém pokusu použil dvě závaží, každé o hmotnosti 14 kg a nechal je klesat 12 krát za sebou z výšky 2 m do nádoby s vodou.
V nádobě byla voda o hmotností 6,7 kg. Při pokusu se teplota vody zvýšila o 0,24 K. Jakou hodnotu měrné tepelné kapacity vody zjistil?
ÚLOHA 2:
V Niagarských vodopádech padá voda z výšky 60 m. Jak se zvýší její teplota, předpokládáme-li, že se celá kinetická energie padající vody změní ve vnitřní energii vody?
ÚLOHA 1:
Změna U konáním práce:
m1 = 14 kg, ΔEp = 2·m1·g·h = 28 kg · 10 m.s-2 · 2 m = 560 J,
ΔU = 12·ΔEp = 6720 J, m2 = 6,7 kg, Δt = 0,24 °C = 0,24 K
Zvýšení teploty:
ÚLOHA 2:

Q = m · c · ∆t
m = hmotnost tělesa
∆t = o kolik stupňů/kelvinů se má ohřát
c = měrná tepelná kapacita (v tabulkách)
ÚLOHA 1:
V elektrické pračce se ohřívá voda o hmotnosti 30 kg. Jaké teplo přijme, zvýší-li se její teplota z 15 °C na 90 °C?
ÚLOHA 2:
Kolik tepla je zapotřebí za ohřátí 4 l vody v železném hrnci hmotnosti 2 kg z 10 °C na 100 °C?
ÚLOHA 3:
Ocelová tyč má tepelnou kapacitu C = 1,5.103J.K-1. Jak se změní její teplota, pokud
a) přijme teplo Q1= 25.103J
b) předá teplo Q2 = 0,45.106J
nabla.cz/soubory/fyzika/priklady/molekulova-fyzika-termika/kalorimetricka-rovnice-teplo.pdf
ÚLOHA 1:
Q = m·c·Δt = 30·4180·(90–15) J = 9,4 MJ
ÚLOHA 2:
ÚLOHA 3:
Teplo Q je skalární fyzikální veličina.
Je určeno energií, kterou při tepelné výměně předá teplejší těleso studenějšímu.
Teplo je dějová veličina, má teplo × přijal/odevzdal teplo
- vedení
- proudění
- záření
Všechna tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb a které na sebe navzájem silově působí. Proto má každé těleso svoji vnitřní energii. Vnitřní energie ovlivňuje vlastnosti a stav látky či tělesa.
Pohybová (kinetická) energie částic se na tělese projevuje jako teplota tělesa, tzn. čím rychleji se jednotlivé částice (atomy, či molekuly) pohybují (kmitají), tím vyšší je teplota tělesa.
Polohová (potenciální) energie částic se na tělese projevuje jako pevnost tělesa, tedy čím větší je polohová energie částic, tím pevnější je těleso, resp. jeho skupenství.
Chemická energie je energie vázaná ve formě chemických vazeb mezi atomy a lze ji uvolňovat nebo naopak vázat pomocí chemických reakcí. I v případě chemických reakcí platí zákon zachování energie, takže součet energie vazeb před reakcí a dodané energie se rovná součtu energie vazeb po reakci a uvolněné energie.
Pokud je chemická energie během reakce uvolněna, děje se tak obvykle ve formě tepla. Mluvíme pak o exotermické reakci. Naopak, pokud se při chemické reakci energie spotřebovává, jde o reakci endotermickou. Klasickým příkladem exotermické reakce je hoření.
Odkud se bere jaderná energie? V jádru atomu se nacházejí protony a neutrony. Tyto částice nazýváme jedním slovem nukleony (z latinského nucleus = jádro). Mezi nukleony v jádru působí přitažlivá jaderná síla, která je až milionkrát větší než odpudivá elektrická síla. Při jaderných reakcích se tyto silné vazby poruší a mění se tak složení a struktura atomových jader. Jadernou energii lze získat jaderným štěpením nebo jaderným slučováním.
přenos vnitřní energie prouděním = pohyb částí hmoty o různé teplotě
sálání (záření, radiace) je fyzikální proces, při kterém látka vysílá do prostoru energii ve formě elektromagnetického záření
Jakmile se nějaký předmět pohybuje, znamená to, že má energii. Energie pohybujícího se tělesa se nazývá energie kinetická (též pohybová energie). Je-li těleso v klidu, má nulovou kinetickou energii. Potenciální energii mají tělesa, která se nacházejí v silových polích jiných těles (např. tíhová potenciální energie) nebo jsou pružně deformovaná (potenciální energie pružnosti).
Součet těchto energií tvoří celkovou mechanickou energii tělesa.
Všechna tělesa se skládají z částic, které vykonávají neustálý a neuspořádaný pohyb (=> mají kinetickou energii) a které na sebe navzájem silově působí (=> mají potenciální energii).
Vnitřní energie tělesa U je pak součtem celkové kinetické energie všech částic tělesa a celkové potenciální energie všech částic tělesa.
značí se c
jednotka J·kg-1·K-1
Energii nelze vyrobit ani zničit, ale pouze přeměnit na jiný druh energie.
ZZE: Při dějích probíhajících v izolované soustavě těles zůstává součet kinetické, potenciální a vnitřní energie těles konstantní.
E = Ek + Ep + U = konst.
liší se mezi jednotlivými látkami i u různých skupenství jedné látky
závisí i na teplotě látky ⇒ v tabulkách se uvádí hodnota při 20 °C
Měrná tepelná kapacita vody je přibližně
c = 4200 J⋅kg-1⋅K-1 = 4,2 kJ⋅kg-1⋅K-1
Další zaokrouhlené hodnoty:
líh 2500 J⋅kg-1⋅K-1
glycerol 2400 J⋅kg-1⋅K-1
sklo700 J⋅kg-1⋅K-1
hliník 890 J⋅kg-1⋅K-1
měď 390 J⋅kg-1⋅K-1
železo 450 J⋅kg-1⋅K-1
zlato 129 J⋅kg-1⋅K-1
Hodnoty se mohou lišit i podle kvality dané látky.
= množství tepla, které musíme dodat 1 kg látky, aby se ohřál o 1 K
= zahřívání nebo ochlazování
= přenos části vnitřní energie z teplejšího tělesa na chladnější
Přírůstek vnitřní energie soustavy (ΔU) je roven součtu práce (W) vykonané okolními tělesy působící na soustavu a tepla (Q) odevzdaného okolními tělesy soustavě.
ΔU = W + Q
Jiný zápis téhož Q = ΔU + W’
Teplo (Q) přijaté soustavou je rovno součtu přírůstku vnitřní energie soustavy (ΔU) a práce (W’), kterou soustava vykoná.
Další formulace:
Nelze sestrojit perpetuum mobile prvního druhu:
Nelze sestrojit stroj, který by trvale dodával mechanickou energii, aniž by spotřeboval odpovídající množství energie jiného druhu.
Měrnou tepelnou kapacitu násobíme hmtností látky a teplotní rozdílem, protože udává množství tepla, které musíme dodat 1 kg látky, aby se ohřál o 1 K
Látka s větší c potřebuje k ohřátí o stejnou teplotu víve tepla.
Látka s větš c se stejným teplem ohřeje o menší teplotu.
W = práce vykonaná okolními tělesy
Q = dodané teplo
ÚLOHA 1:
Při stlačení plynu uzavřeného v nádobě s pohyblivým pístem byla vykonána práce 2,5 kJ, plyn byl současně ohříván tak, že přijal teplo 1,2 kJ. Jak se při tomto ději změnila vnitřní energie plynu?
ÚLOHA 2:
Termodynamická soustava přijme z okolí teplo 3,6 kJ a současně vykoná práci 2,9 kJ. Jak se změní vnitřní energie soustavy?
ÚLOHA 3:
Plyn v pracovním válci vykonal práci 8 kJ a současně odevzdal teplo 2,5 kJ. Vypočtěte změnu jeho vnitřní energie. Jak se to projeví na teplotě plynu?
ÚLOHA 1:
Q = +1,2 kJ (plyn přijímá teplo)W = +2,5 kJ (práci koná okolí)
ΔU = W + Q = 1,2 kJ + 2,5 kJ = 3,7 kJ
Zvýšila se o 3,7 kJ.
ÚLOHA 2:
Q = +3,6 kJ (soustava přijímá teplo)W = −2,9 kJ (práci koná soustava)
ΔU = W + Q = 3,6 kJ − 2,9 kJ = 0,7 kJ
Zvýší se o 0,7 kJ.
ÚLOHA 3:
W = −8 kJ (plyn koná práci) Q = −2,5 kJ (plyn odevzdává teplo)
ΔU = W + Q = −8 kJ − 2,5 kJ = −10,5 kJ Snížila se o 10,5 kJ.
U plynu je zanedbatelná vnitřní potenciální energie, proto se snížení projeví na kinetické energii = sníží se teplota.
Jedná se o úlohy na tepelnou výměnu mezi dvěma a více tělesy.
Typicky se ptáme na výslednou teplotu po smíchání dvou kapalin nebo ponoření tělesa do kapaliny.
Můžeme počítat i počáteční teplotu, hmotnost nebo měrnou tpelnou kapacitu některého z těles.
- používá se na měření tepla za pomocí tepelně izolované nádoby
- umožňuje pokusně provádět tepelnou výměnu mezi tělesy
Dvě nádobky vloženy do sebe, mezi stěnami je vzduch, který tepelně izoluje vnitřní nádobku od vnější a od okolí. Nádobky jsou překryty víčkem s otvorem pro teploměr a míchačku.
https://www.youtube.com/watch?v=o0z1B0zDhBQ
https://old.vscht.cz/fch/prikladnik/zkhtml/math/d59.gif
https://cs.wikipedia.org/wiki/Perpetuum_mobile
https://edu.techmania.cz/cs/encyklopedie/fyzika/plyny/druhy-termodynamicky-zakon/perpetuum-mobile
http://utf.mff.cuni.cz/popularizace/eter/Perp-mobile-4.pdf
teplo přijaté 1. látkou = teplo odevzdané 2. látkou
Q1 = Q2
m1·c1(t − t1) = m2·c2(t2− t)
∆t = větší teplota − menší teplota
ÚLOHA 1:
nabla.cz/soubory/fyzika/priklady/molekulova-fyzika-termika/kalorimetricka-rovnice-vody2.pdf
ÚLOHA 2:
Závaží o hmotnosti 500g z neznámého prvku o teplotě 100 °C vhodíme do 2 litrů vody o teplotě 20 °C. Teplota vody a závaží se ustálila na 24 °C . Urči měrnou tepelnou kapacitu a druh prvku.
ÚLOHA 3:
Ve vaně je 220 litrů vody o teplotě 55 °C. Kolik vody o teplotě 14 °C musíme do vany přilít, aby výsledná teplota vody byla 40 °C? (127 l)
ÚLOHA 4:
Kolik studeného čaje o teplotě 20 °C musíme nalít do 0,25 l horkého čaje o teplotě 80 °C, abychom získali snesitelně teplý nápoj o teplotě 45 °C? (0,35 l)
ÚLOHA 1:
Stlačený vzduch v pístu pumpičky (jeho teplota se rovná teplotě místnosti) nadzvedne píst.
ÚLOHA 2:
Do ledničky dáme uzavřenou skleněnou láhev s plynem a necháme ji chladnout.
ÚLOHA 3:
Z ledničky vynadáme balónek a necháme ho v místnosti ohřát. Balónek se rozpíná.
ÚLOHA 4:
Rozžhavené spaliny v pístu motoru roztlačují píst.
úLOHA 1: Stlačený píst

ÚLOHA 2: Uzavřená lahev
W = 0 (práce se nekoná),
Q < 0 (plyn se v ledničce ochlazuje),
∆U < 0

ÚLOHA 3: Balonek z ledničky
W < 0 (balónek zvětšuje objem ⇒ koná práci odtlačováním okolí),
Q > 0 (vzduch se ohřívá od teplejšího okolí),
∆U > 0 (teplota plynu se zvýší)
ÚLOHA 4: Spaliny v motoru

Výpočet koncové teploty:
Výpočet počáteční teploty:
ÚLOHA 1:
nabla.cz/soubory/fyzika/priklady/molekulova-fyzika-termika/kalorimetricka-rovnice-vody.pdf
ÚLOHA 2:
Železné závaží o hmotnosti 200 g hodíme do 0,5 litru vody o teplotě 20 °C. Teplota vody se ustálila na 22 °C. Jaká byla původní teplota závaží?
c1 = 4200 J⋅kg-1⋅K-1 , m1 = 0,5 kg, t1 = 20 °C, c2 = 450 J⋅kg-1⋅K-1 , m2 = 0,2 kg , t = 22 °C, t2 = ?
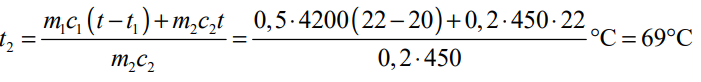
ÚLOHA 3:
K určení průměrné teploty tavící pece do ní byla vložena platinová koule o hmotnosti 100 g. Po vytažení byla koule ponořena do 1 kg vody o teplotě 10 °C. Teplota vody stoupla na hodnotu 14 °C. Jaká byla teplota v peci?
ÚLOHA 4:
Do 200 ml vody o teplotě 20 °C (pokojová teplota) přilijeme 150 ml vody o teplotě 80 °C (horká voda). Určete výslednou teplotu vody.
teplo přijaté/odevzdané
1. látkou + 2. látkou + 3. látkou + ... = 0
Q1 + Q2 + Q3 + … = 0
m1·c1(t − t1) + m2·c2(t − t2) + m3·c3(t − t3) + … = 0
t = výsledná koncová teplota
∆t = koncová teplota − počáteční teplota
přijaté teplo vyjde +
odevzdané teplo vyjde −
př. zahřátí rukou třením nebo tleskáním
Výpočet koncové teploty:
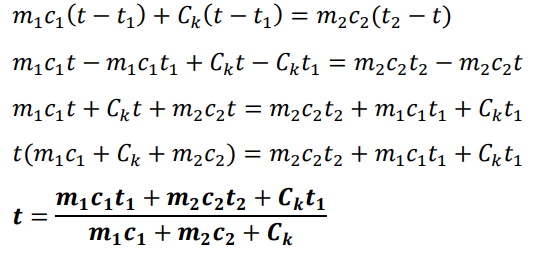
nabla.cz/soubory/fyzika/priklady/molekulova-fyzika-termika/kalorimetricka-rovnice-kalorimetr2.pdf
ÚLOHA 1:
Kalorimetr o tepelné kapacitě 63 J⋅K-1 obsahuje 250 g oleje o teplotě 12 °C. Do oleje v kalorimetru vložíme měděné závaží o teplotě 100 °C a hmotnosti 500 g . Po ustálení má vše teplotu 33 °C. Urči měrnou tepelnou kapacitu oleje.
m1 = 0,25 kg , t1 = 12 °C, c1 = ?
m2 = 0,5 kg, t2 = 100 °C, c2 = 380 J⋅kg-1⋅K-1,
t = 33 °C, C = 63 J⋅K-1
Olej v kalorimetru má měrnou tepelnou kapacitu 2200 J⋅kg-1⋅K-1
ÚLOHA 2:
Do měděného kalorimetru o hmotnosti 128 g, ve kterém je 240 g vody o teplotě 8,4 °C, ponoříme kousek neznámého kovu o hmotnosti 192 g zahřátého na teplotu 100 °C. Vypočtete měrnou tepelnou kapacitu tohoto kovu a určete, o jaký kov se jedná, jestliže se teplota v kalorimetru ustálila na hodnotě 21,5 °C.
ÚLOHA 3:
Měděný kalorimetr má hmotnost 0,32 kg a je v něm voda o objemu 0,25 l a teplotě 291 K. Hliníkový váleček o hmotnosti 0,08 kg byl zahřát na teplotu 372 K a ponořen do kalorimetru. Výsledná teplota byla 295,5 K. Stanovte měrnou tepelnou kapacitu hliníku a srovnejte ji s tabulkovou hodnotou. (864 J⋅kg-1⋅K-1)
Výrobce kalorimetru často certifikuje tzv. tepelnou kapacitu C, tedy veličinu, která říká kolik tepla potřebuji k ohřátí tělesa o 1 °C.
Tato veličina se na rozdíl od měrné tepelné kapacity nevztahuje na 1 kg látky, ale na celé těleso. Proto je její jednotkou J/°C a nahrazuje součin m.c:
m1·c1(t − t1) + C(t − t1) = m2·c2(t2− t)
Počáteční teplota kalorimetru je stejná jako teplota kapaliny v něm.
Sledujeme změny energie během pádu míčku:
• Míček padá ⇒ potenciální energie se zmenšuje.
• Během pádu se jeho pád zrychluje ⇒ kinetická energie se zvětšuje.
Míček se odrazí a začne stoupat.
Po každém odrazu se míček odrazí do menší výšky
⇒ jeho celková mechanická energie se postupně zmenšuje.
Zvýšila se teplota míčku, podlahy a vzduchu ve třídě = mechanická energie míčku se změnila na vnitřní energii soustavy míček-vzduch-podlaha = zvýšila se rychlost neuspořádaného pohybu částic = zvýšila se kinetická energie jejich neuspořádaného pohybu.
Auto se rozjíždí = chemická energie paliva se mění na kinetickou energii auta.
Auto brzdí = kinetická energie auta se mění na vnitřní energii brzd (zahřívají se, jejich částice se rychleji pohybují).
Zahřívání rukou třením = částice se rozpohybují rychleji
Zahřátí rukou tleskáním = částice se stlačením vychýlí z rovnovážné polohy, návratem zpět se rozpohybují.
Shoření meteoru v atmosféře = opět dojde ke zvýšení rychlosti částic, teplota se zvýší natolik, že začne hoření a uvolní se chemická energie
ÚLOHA 1:
Urči změnu vnitřní energie soustavy, pokud se student o hmotnosti 70 kg spouští po tyči z výšky 3,5 m. Proč je bezpečnější dolů ručkovat než se spouštět dolů?
ÚLOHA 2:
Tenisový míček o hmotnosti 50 g, který padal volným pádem z výšky 1 m, vyskočil po odrazu od podložky do výšky 0,6 m. Vysvětlete tento děj z hlediska zákona zachování energie a určete při tom ději celkovou změnu vnitřní energie míčku a podložky.
ÚLOHA1:
m = 70 kg, h = 3,5 m, ∆U = ?
∆U = ∆Ep = mgh = 70⋅10⋅3,5 J = 2450 J
Student má potenciální energii, která se změní na přírůstek vnitřní energie rukou a tyče o 2450 J.
Pokud se spouštíme zahřívá se pouze malá část rukou a tak se může teplota této části pokožky značně zvýšit. Když dolů ručkujeme, zvyšuje se vnitřní energie svalů, kterých je daleko více a tak se jejich teplota zvýší méně.
ÚLOHA 2:
m = 70 kg, h = 3,5 m, ∆U = ?
∆U = ∆Ep = mgh1 − mgh2 = 0.05⋅10⋅0,4 J = 0,2 J
Vnitřní energie vzrostla o 0,2 J.
ÚLOHA 1:
Automobil o hmotnosti 1600 kg jedoucí rychlostí 90 km/h prudce zastaví. U kterých těles se zvýší jejich vnitřní energie? Jak?
ÚLOHA 2:
Ocelový hřebík o hmotnosti 50 g byl zaražen do prkna 20 údery kladiva. Hmotnost kladiva byla 0,5 kg a jeho dopadová rychlost 12 m.s−1. O kolik se zvýšila energie hřebíku?
Budeme předpokládat, že se kladivo při každém úderu do hřebíku zcela zastaví.
ÚLOHA 1:
Zvýší se vnitřní energie brzdných kotoučů, brzdného obložení, pneumatik, silnice, vzduchu. Změna vnitřní energie těchto těles odpovídá původní kinetické energii auta.
m = 1600 kg, v = 90 km⋅h-1 = 25 m⋅s-1, ∆U = ?
Vnitřní energie soustavy se zvýšila o 0,5 MJ.
ÚLOHA 2:
m = 0,5 kg, v = 12 m⋅s-1, ∆U = ?
Energie hřebíku a kladiva se zvýšila o 720 J.