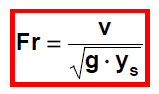Hydraulika Proudění s volnou hladinou
Created by Nikol Vypior (osobní/personal)
Poznámky z hodin HYA2 na FSv ČVUT. Obrázkové materiály jsou duševním vlastnictvím doc. Ing. Aleše Havlíka, CSc.
#hydraulika, #hydrodynamika, #proudění

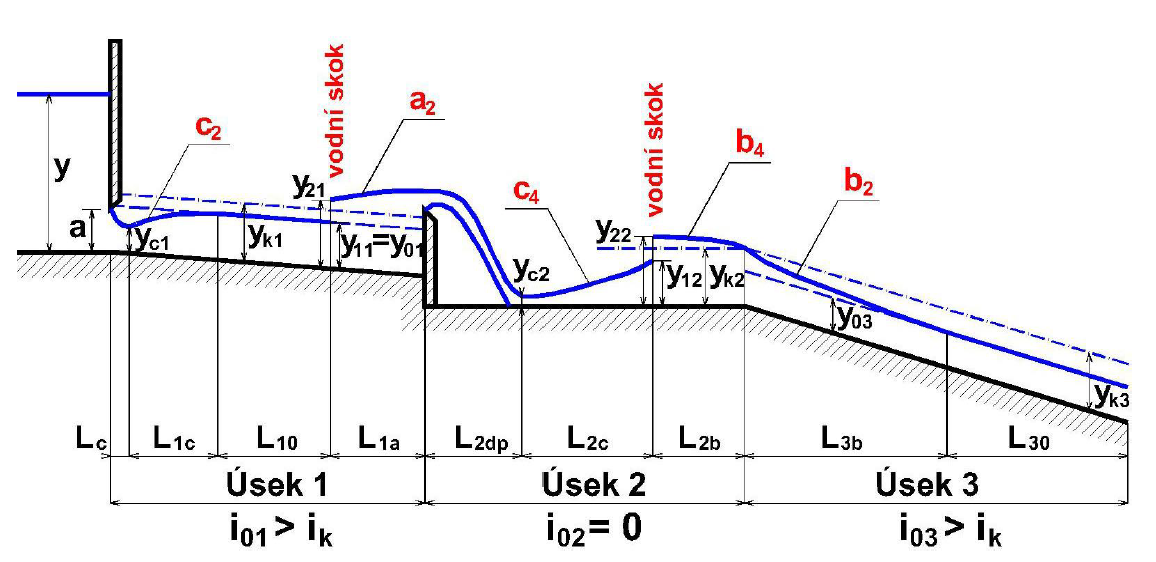
ŘEŠENÍ CHARAKTERISTICKÉHO PRŮBĚHU HLADIN

vs.
Trojúhelníkové měrné přelivy
Kapaliny
- kapaliny téměř nestlačitelné (zvýšení tlaku o 105Pa zmenší objem o 5%)
- za normálních tlaků považujeme za nestlačitelné
- tvoří volnou hladinu, nevyplňuje celý prostor (nerozpínavé)
Plyny
- značně stlačitelné
- rozpínavé - snaží se vyplnit celý prostor, do něhož mohou proniknout (→ tlka plynu na stěny nádoby
Obdélníkové měrné přelivy
Rce pro trojúhelníkový profil
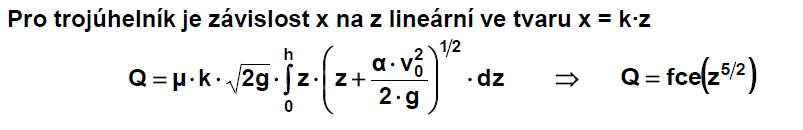
Přes jezová tělesa

📑 HYA2 - Hydraulika potrubí
Rce pro obdélníkový profil
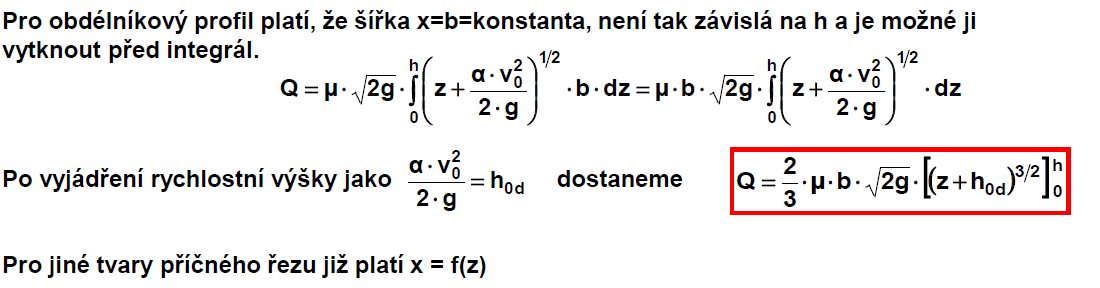

Rce přepadu

Přes širokou korunu

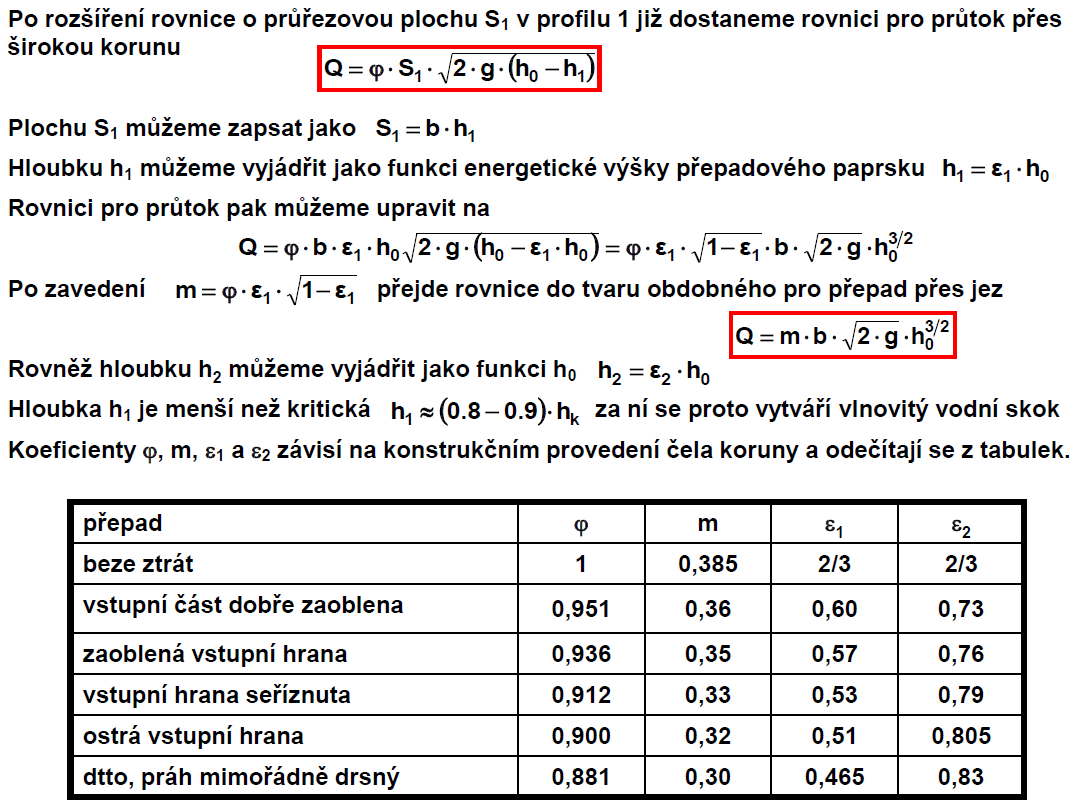
Typy

Popis přepadu
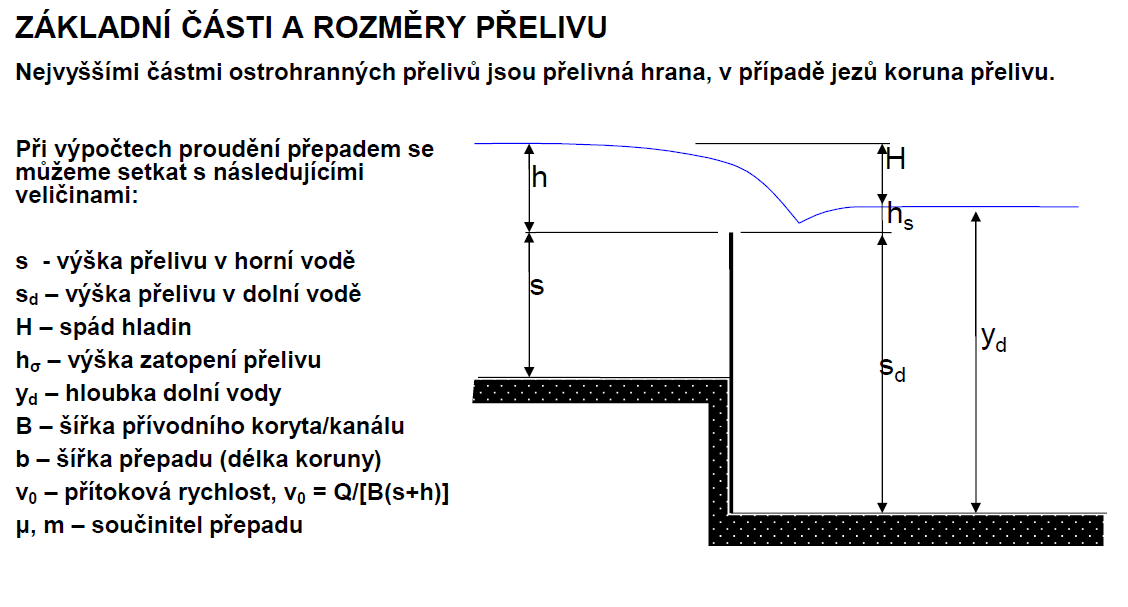
Dokonalý vs. NEdokonalý
NEdokonalý = hladina dolní vody vyšší než koruna přelivu

Přepady
= hydraulický jev
vs. přeliv = vlastní konstruckce, kde voda přepadá
Členění
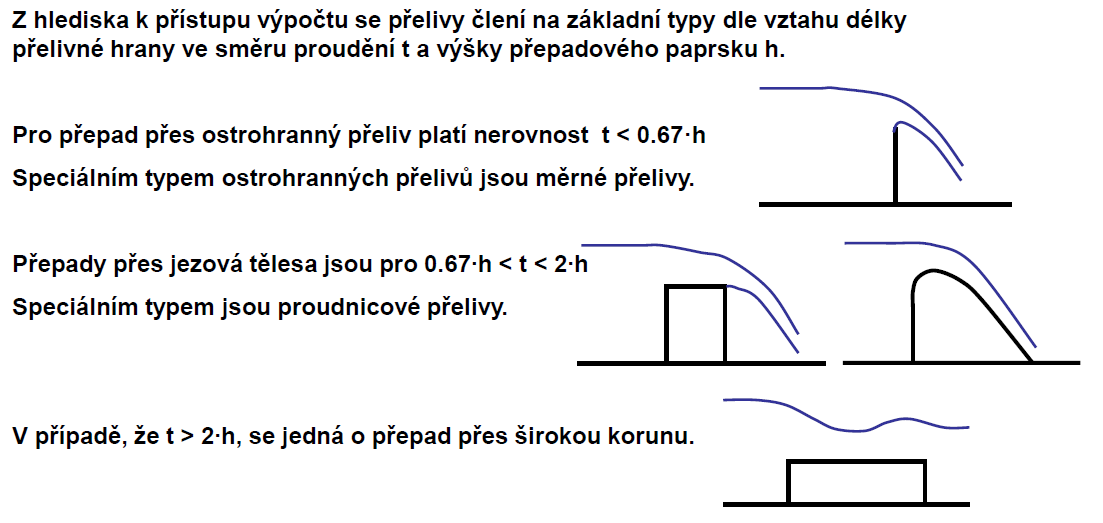
PRIZMATICKÁ KORYTA
změna hloubky:
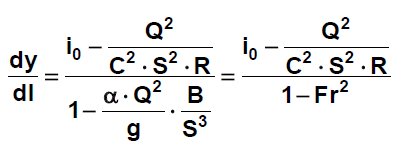
neboť:
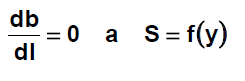
Prizmatické koryto: tvar průřezu, drsnost omočeného obvodu a sklon dna jsou konstantní, tj. neměnné po délce koryta.
Proudění mostními objekty a propustky
Tvar paprsku
VS při změně dna
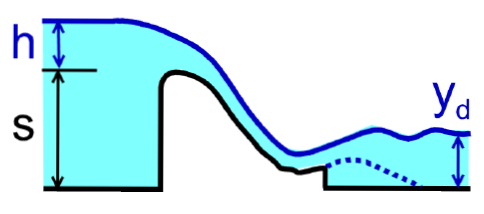
VS přilehlý
HYDRAULICKÉ ŘEŠENÍ KORYT

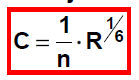


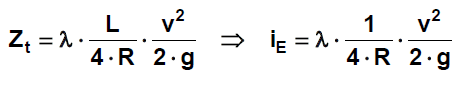
Vliv zatopení dolní vodou
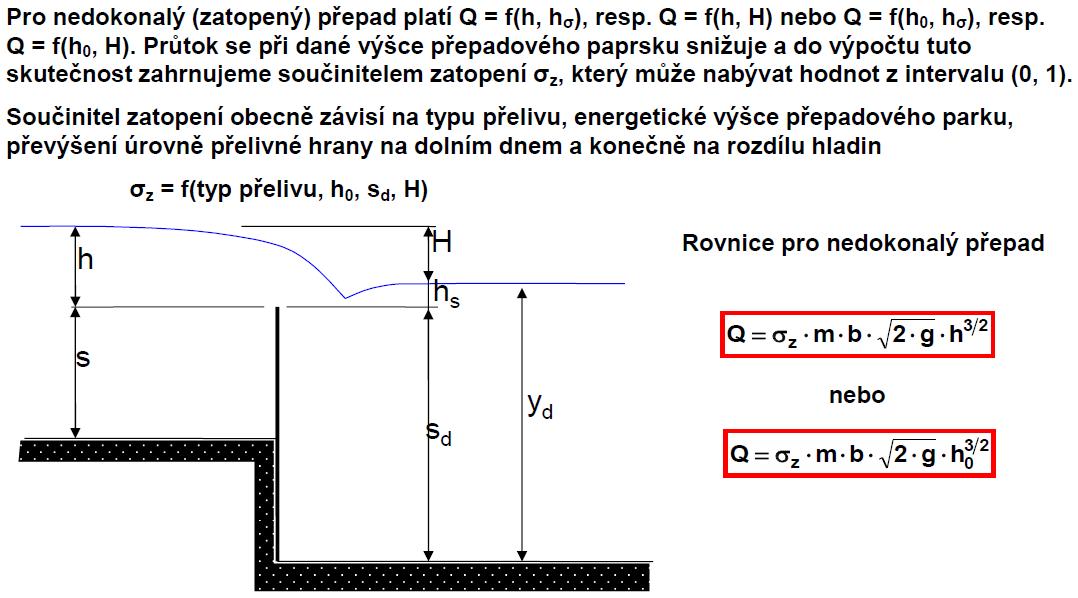
VS oddálený
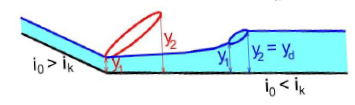
ROVNOMĚRNÉ PROUDĚNÍ
Podmínky:
- prizmatické koryto
- rovnost sklonu dna, hladiny a čára energie (i0 = i = iE)
- S = konst.; y = konst.
Neustálené proudění
VS přiblížený
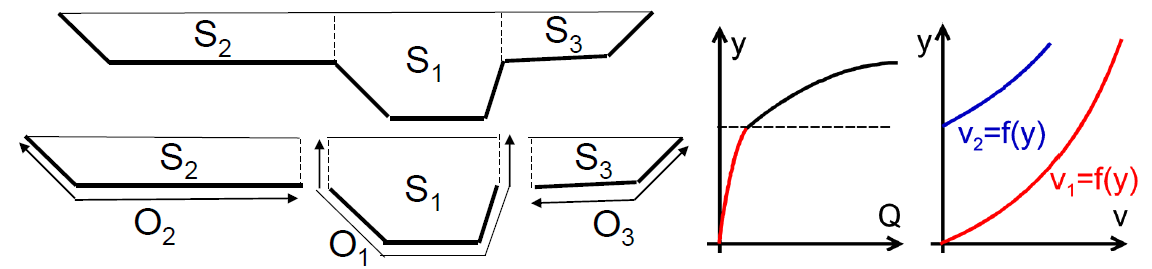
SLOŽENÉ PROFILY
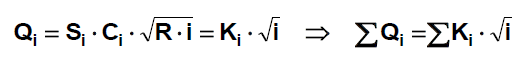
při přechodu režimů proudění
- přechod říční ► bystřin. se děje PLYNULE
- přechod bystřin. ► říční VODNÍ SKOK
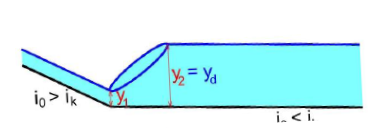
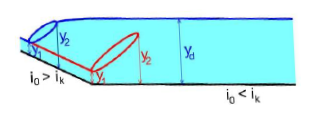
Určení polohy VS
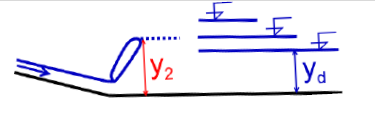
polohu vodního skoku získáme porovnáním y2 předpokládaného přilehlého vodního skou s hloubkou dolní vody yd
Rce změny hloubky vody v podélném směru pro prizmatické koryto
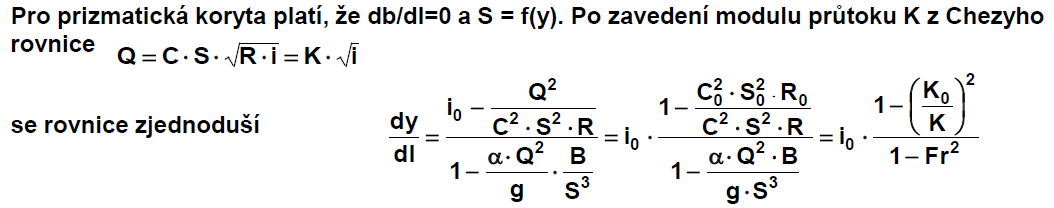
veličiny s indexem 0 platí pro rovnoměrné proudění

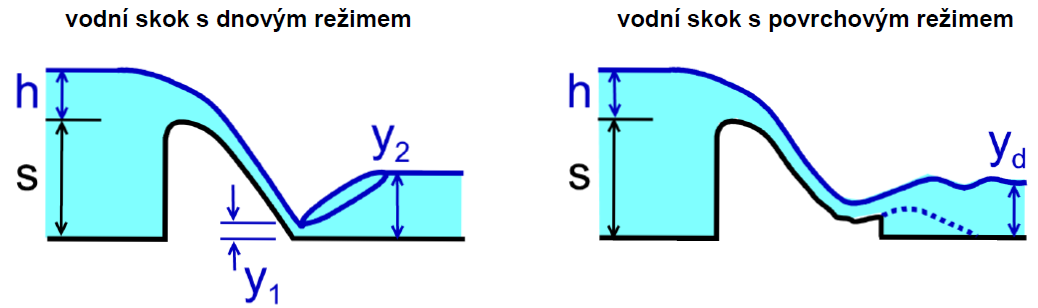
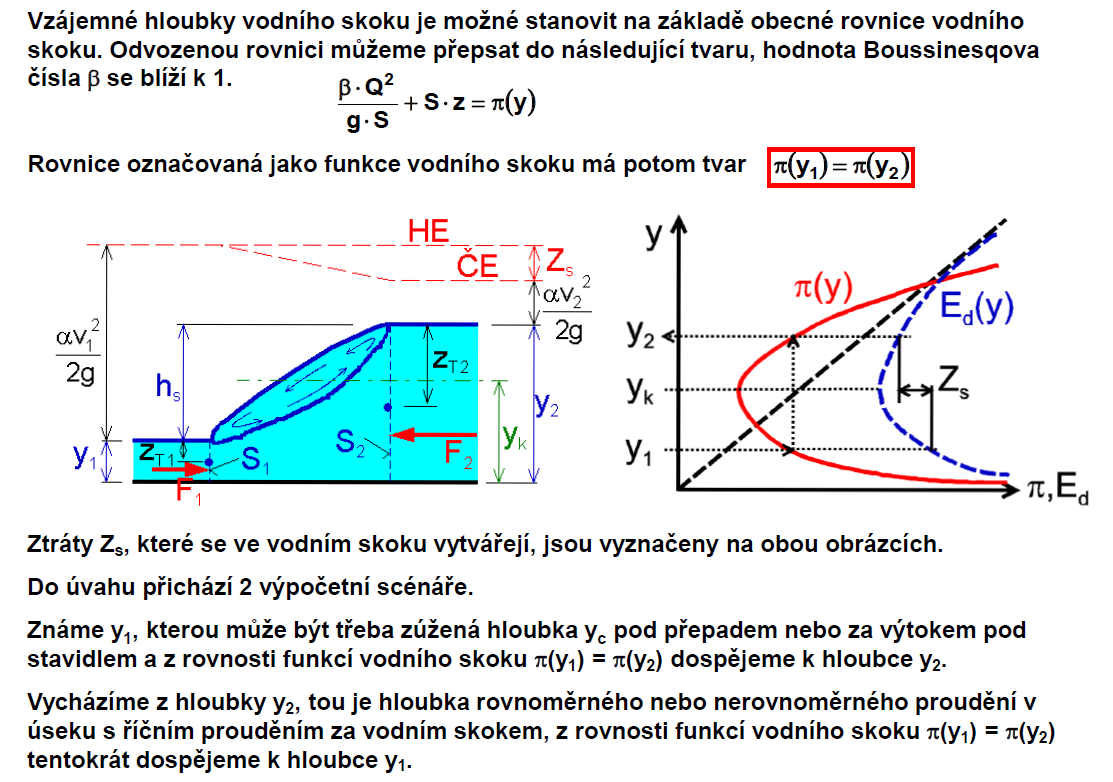
Charakteristiky VS
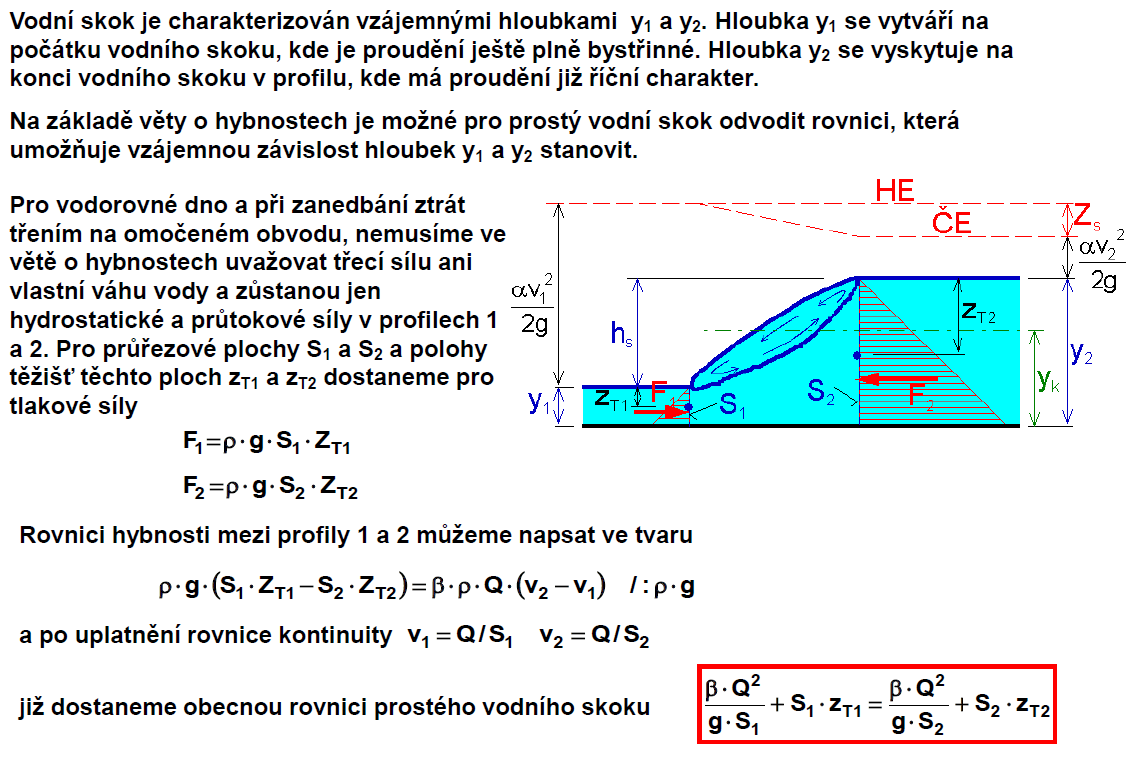
Prostý VS v obdélníkovém korytě

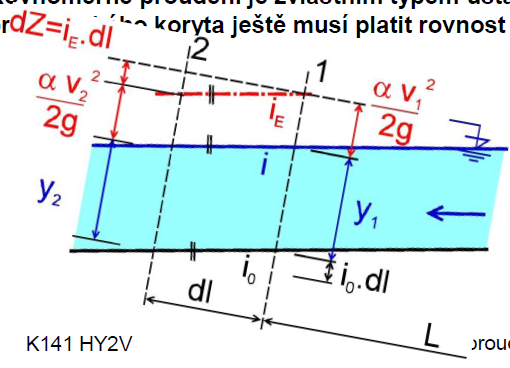
NEROVNOMĚRNÉ PROUDĚNÍ
- 1D proudění v korytech vodních toků
- sklon čáry energie není rovnoběžný se sklonem hladiny
- v podélném směru SE MĚNÍ geometrické charakteristiky (průřezová plocha, omočený obvod, hydraulický poloměr)
Ustálené proudění
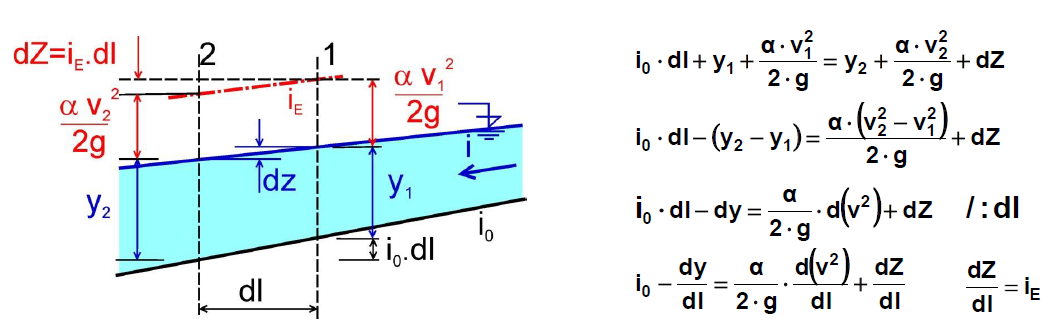
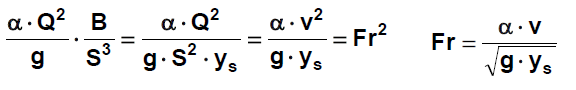


Legenda:
- Q ... objemový průtok korytem,
- v ... střední (průřezová) rychlost v příčném profilu koryta,
- y … hloubka proudu,
- t ... čas,
- x ... vzdálenost podél délky koryta
Vodní skok s povrchovým režimem
hledání vzdálenosti

Vodní skok
- dochází k němu při přechodu z bystřinného na říční proudění
- doprovázeno intenzivní turbulencí s rozsáhlými vírovými válci zpravidla s vodorovnou osou
- dochází k tlumení (disipaci) kinetické energie


Vzájemné hloubky VS
Za objektem
Výpočet NP prizmatické koryto
- ztráty pouze třením
- nedochází k rozšiřování/zužování - neuvažují se místní ztráty
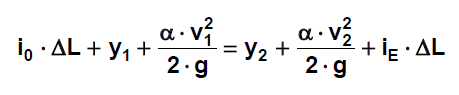
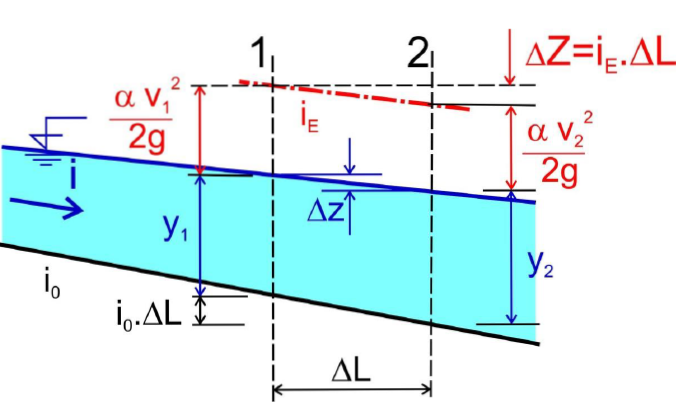
Dva přístupy k řešení:
- pro zvolený rozdíl hladin hledám vzdálenost
- z dané vzdálenosti hledám rozdíl úrovní hladiny (iteracční postup)
Výpočet NP
- diferenciální rovnice - Bachmětěv, Pavlovskij, Van Te Chow
- nyní pomocí Bernoulliho rce - popis ztrát třením mezi 2 profily na vzdálenosti L pomocí průměrného sklonu čáry energie (hydraulického sklonu) iE
- volně dostupné matematické modely
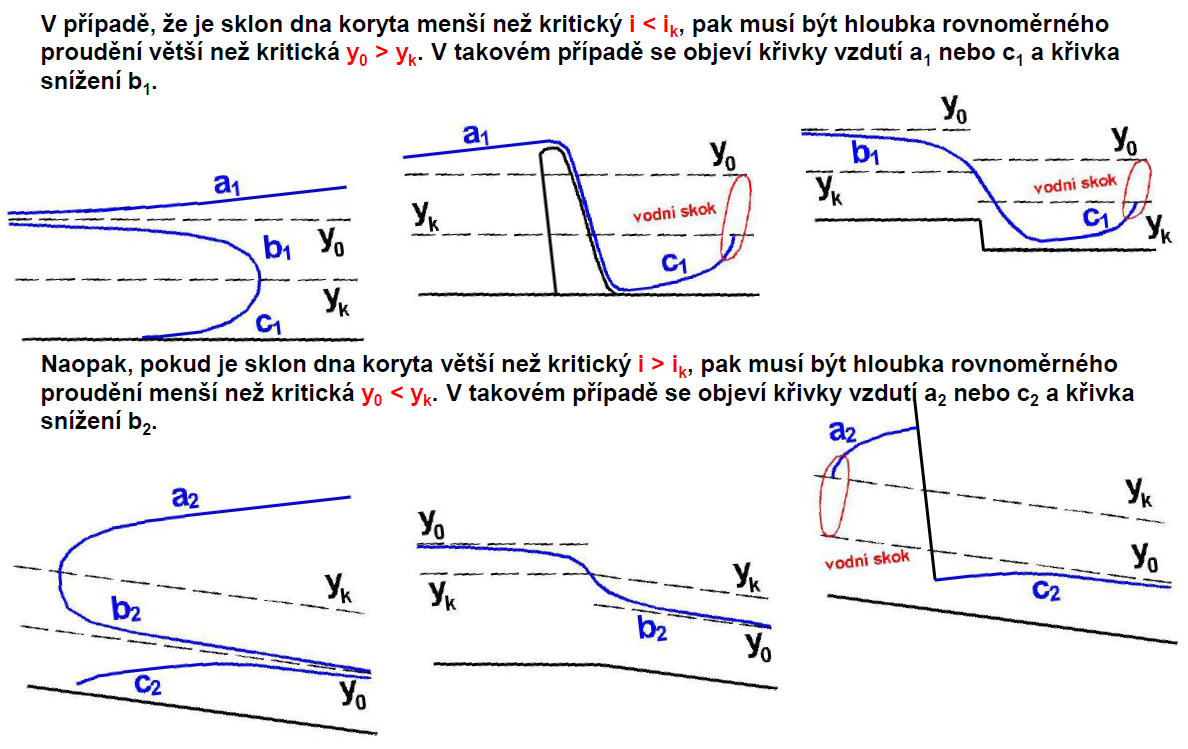
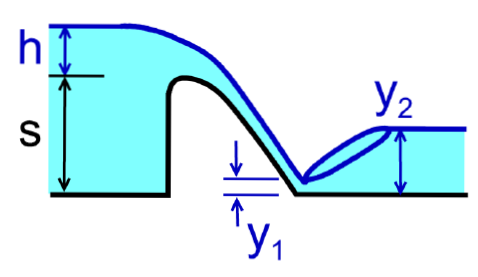
Charakteristické průběhy hladin
kritická hloubka

Dochází k jejímu dosažení při přechodu z říčního na bystřinné proudění.
hledání rozdílu hladin

Metoda po úsecích
- říční proudění ► výpočet PROTI proudu
- bystřinné p. ► výpočet PO proudu
Potřebuji znát úroveň hladiny ve spodním profilu - pro říční proudění - a dopočítávám hladinu v horním profilu, který je novým spodním profilem pro další úsek. Bystřinné proudění obráceně.
Coriolisovo číslo
- Pro pravidelná koryta se doporučuje používat a v rozsahu 1.0 až 1.1.
- Pro nepravidelná koryta však mohou nastat hodnoty až α = 1.3 až 1.8.
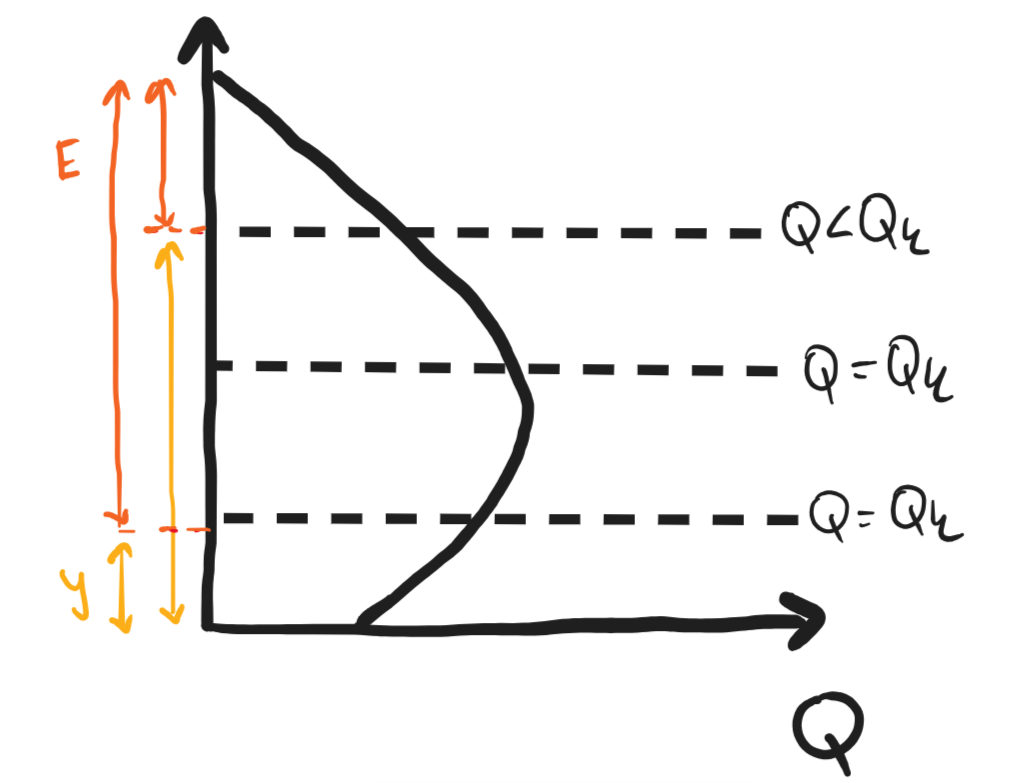
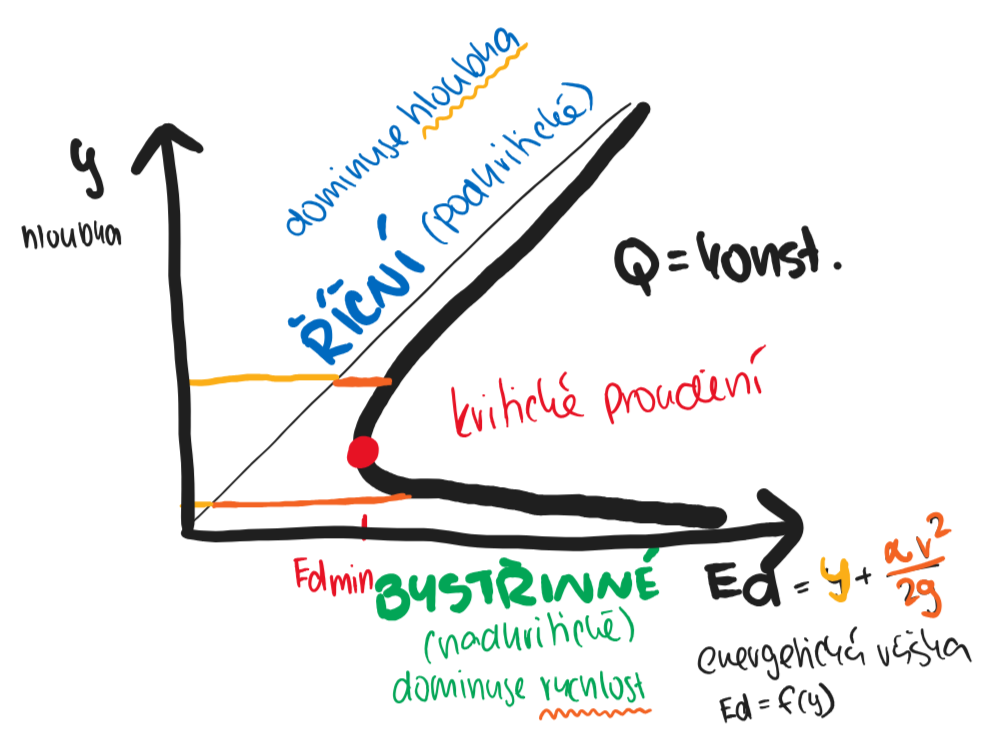
Parabola průtoku
maximální Q (průtok) při kritickém proudění
Potenciální zúžená hloubka yc pod jezem (iterace)

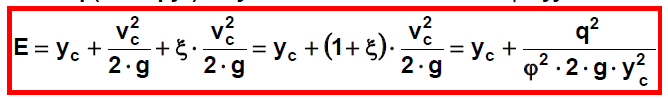
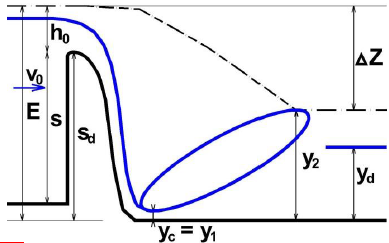
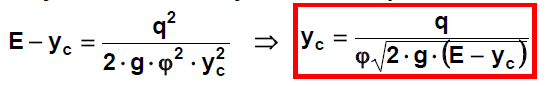
Tlumení kinetické energie
Výpočet NP přirozené (neprizmatické) koryto
- mění se tvar, rozměry, odpory ► S, O, R nelze vyjádřit analyticky
- profily se známou vzdálenostíod sebe
- musíme znát jednu výchozí hloubku (u říčního proudění y2)
- zahrnujeme i ztráty místní

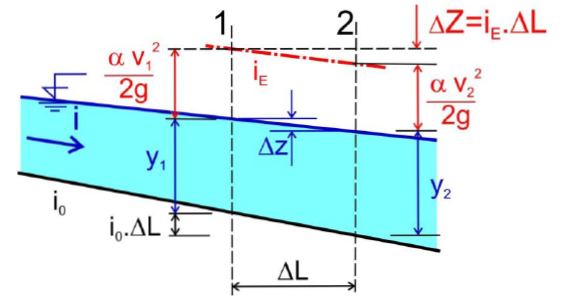
Rce změny hloubky vody v podélném směru pro neprizmatické koryto
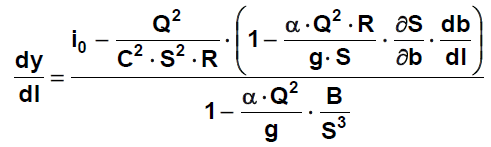
Vodní skok s dnovým režimem
Iterační postup

Froudovo číslo
pro určení režimu proudění a pro stanovení kritické hloubky
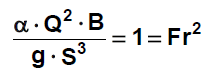
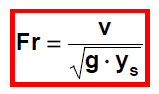

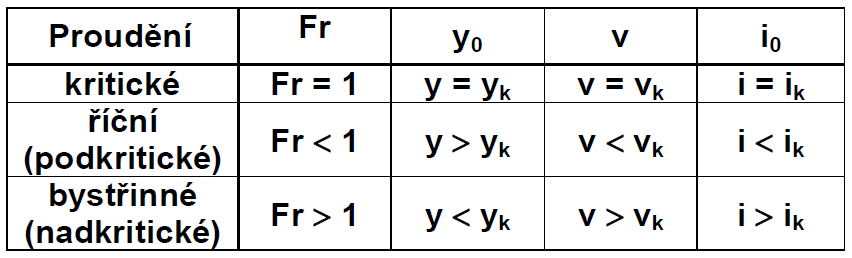
g - gravitační zrychelní [m/s2]
ys - střední hloubka (obecně jinak charakterisitický rozměr l) [m]
TVAR HLADINY DLE PROUDĚNÍ A SKLONŮ
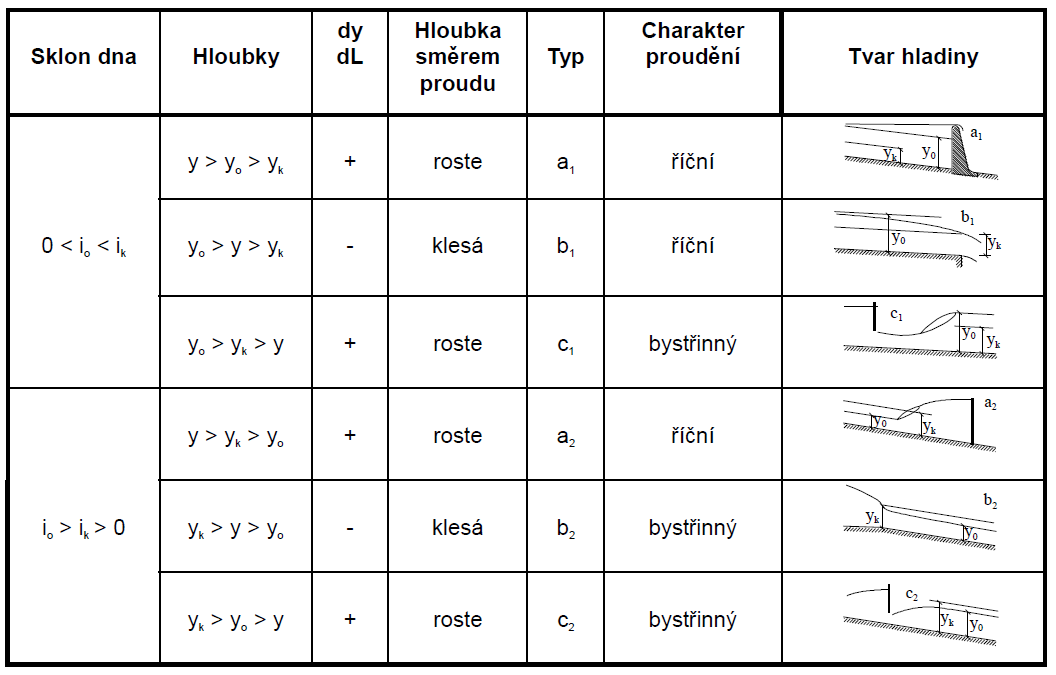
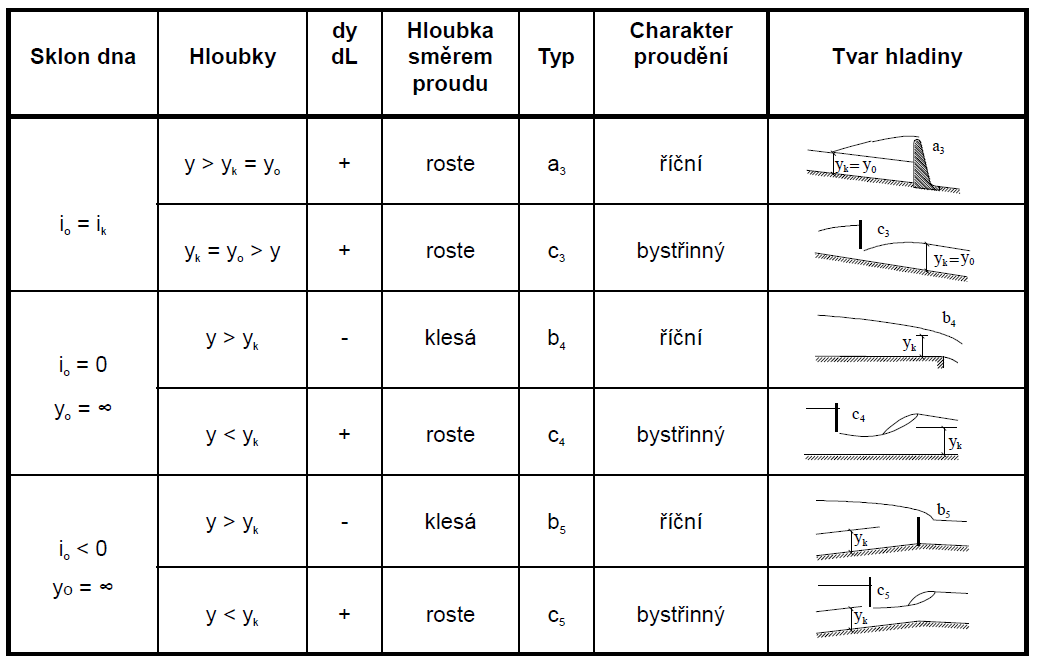
Charakter proudění
Režimy či druhy proudění:
- říční (podkritické)
- bystřinné (nadkritické)
- kritické
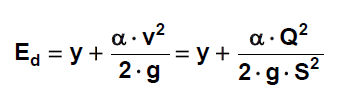
Výpočet vzduté hladiny nad mostem pomocí BR
Místní ztráty

Neustálené proudění
mění se i v čase, ne pouze v prostoru
- rychle proměnné = rázové vlny
- pomalu proměnné - např. povodňové vlny
Vlny
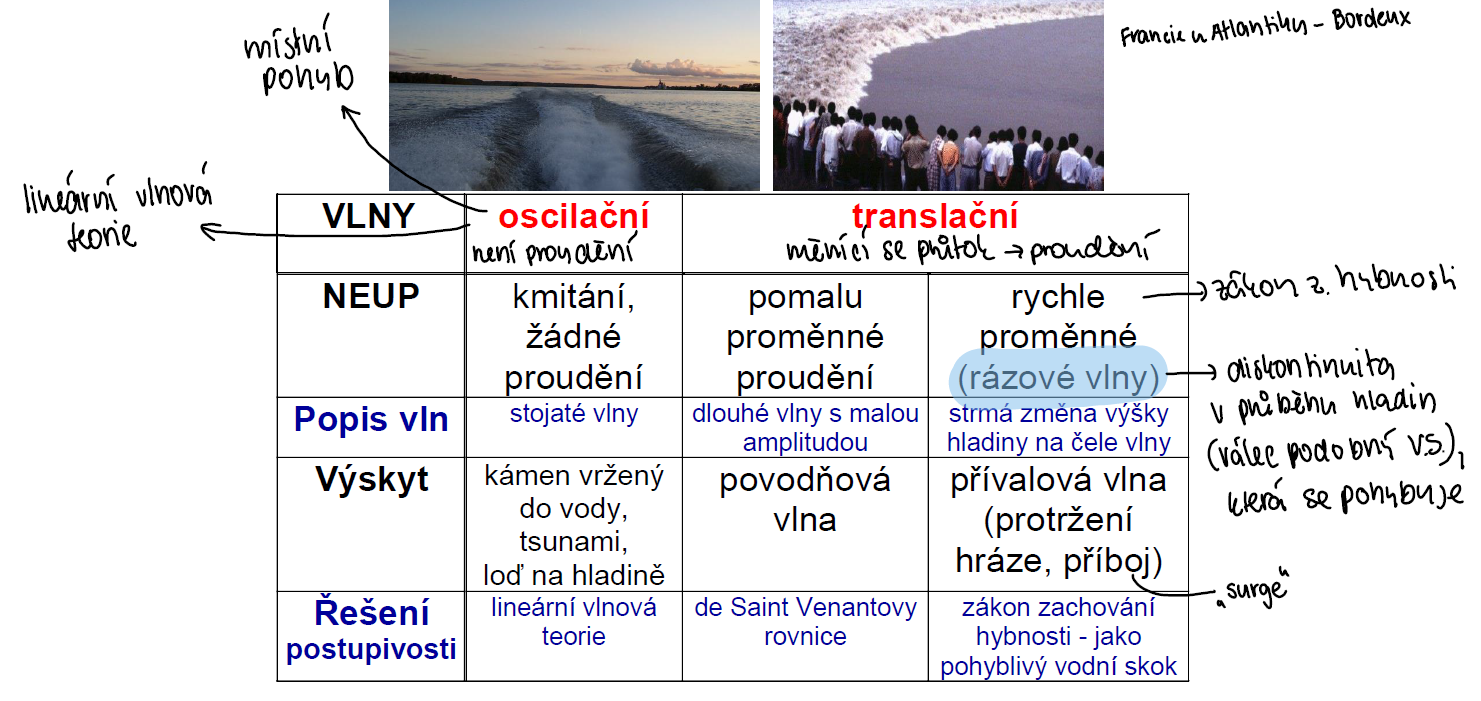
https://personalpages.manchester.ac.uk/staff/david.d.apsley/lectures/hydraulics3/OCFRvf.pdf
Rázové vlny
- translační vlny (transportují hmotnost vody) vznikající při rychle se měnícím proudění (typicky změna průtoku způsobena regulací průtoku objektem, např. stavidlem, jinak třeba příbojem moře)
- vlny se pohybují větší rychlostí než je rychlost proudění vody (tj. než je rychlost šíření charakteristik)
- lze je chápat jako analogii rázových vln, které vznikají ve vzduchu při překročení rychlosti zvuku (sonický třesk)
- na rozdíl od pomalu se měnícího proudění vzniká nespojitost hladiny (pohyblivý vodní skok) - z pohledu pozorovatele stojícího na břehu
- jak vyjádřit postupivost?
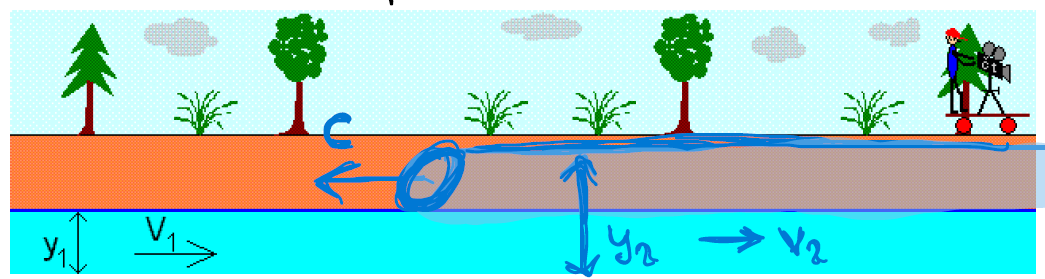
-
k popisu nelze použít de Saint Venantovy rovnice
- např. Příbojová vlna šířící se od moře proti proudu řeky
Petitcodiac river, near Moncton (Bay of Fundy, Canada); Příbojová vlna na řece Qiantang River, poblíž Hangzhou v Číně.
Pozorovatel se bude pohybovat spolu s vlnou rychlostí c:
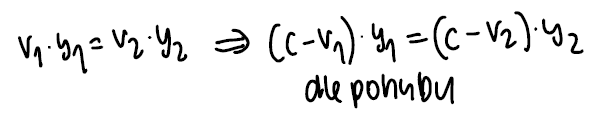
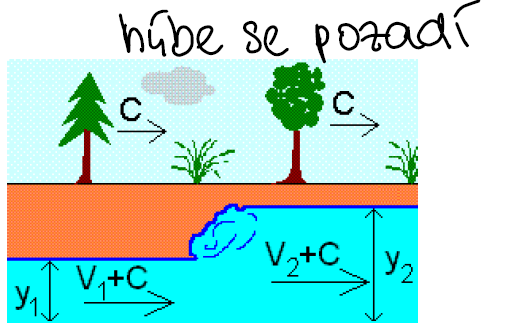
Pak jako klasický vodní skok - doszují se transformované rychlosti.
Vlna snížení
- vlna poklesu proti proudu = záporná zpětná vlna
jev: šíří se korytem při náhlém zvětšení průtoku na dolním konci úseku,
efekt: prázdnění nadrženého prostoru nad stavidlem,
příklad: otevření stavidla na konci úseku koryta
Typy rázových vln
- kladná - vede ke zvýšení hloubky
- záporná - snížení hladiny
- přímá - šíří se ve směru proudění
- zpětná - proti proudu
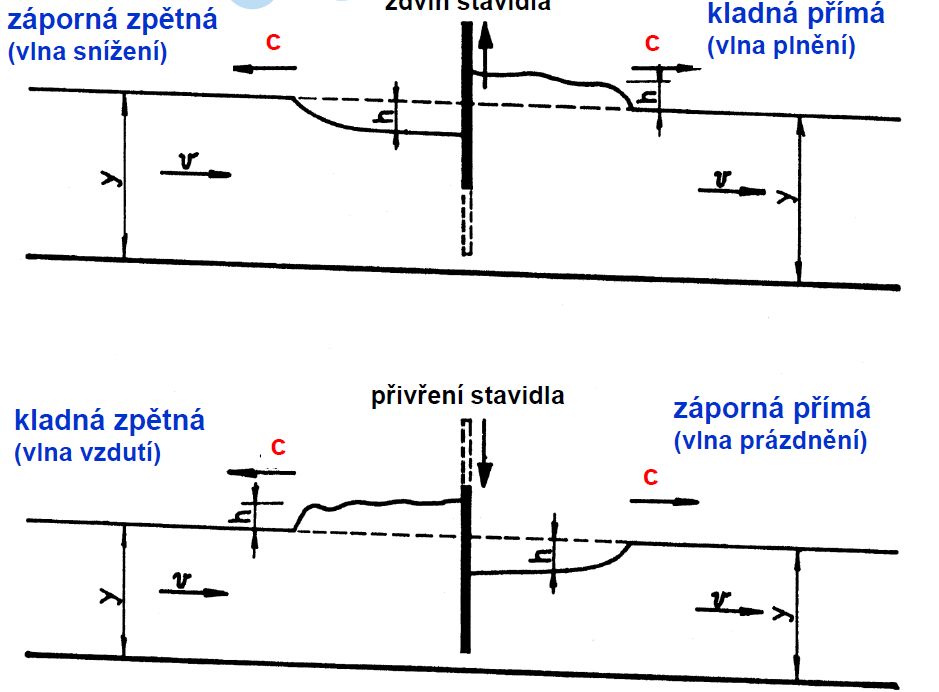
- (vlna snížení, plnění, vzdutí, prázdnění)
- rychlost šíření c záleží na rozdílu rychlostí a hladin
Vlna plnění
- vlna zdvihu po proudu = kladná přímá vlna
jev: šíří se korytem při náhlém zvětšení průtoku na horním konci úseku,
příklad: otevření stavidla na začátku úseku koryta.

Vlna vzdutí
- vlna zdvihu proti proudu = kladná zpětná vlna
jev: šíří se korytem při náhlém zmenšení průtoku na dolním konci úseku,
příklad: uzavření stavidla na konci úseku koryta

Vlna prázdění
- vlna poklesu po proudu = záporná přímá vlna
jev: šíří se korytem při náhlém zmenšení průtoku na horním konci úseku,
efekt: prázdnění koryta pod stavidlem,
příklad: přivření stavidla na začátku úseku koryta.
Viskozita
= vazkost = odpor tekutiny proti změně tvaru
- potřeba když tekutina není v rovnováze a přizpůsobuje se vnějším silám na tekutinu působícím
- u rovnováhy se síly viskozity neuplatňují
- síla viskozity má snahu zseabit rozdíl (vzájemných) rychlostí v proudící tekutině → vnitřní tření
- u malých viskozit můžeme zanedbat → neviskózní tekutina = dokonalá tekutina